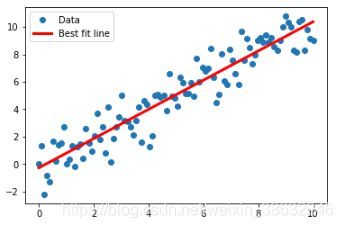
【详细】使用正定分解矩阵拟合线性一次方程
1.如何对方程 A X = b AX=b AX=b求解,A=[x1,x2,x3,…xn], b=[y1,y2,y3…yn]都为列向量。
输入A,b的散点图如下:
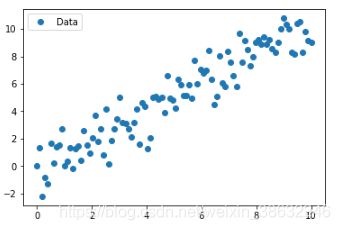
数学推导如下:
令 C = A T ∗ A 令C=A^{T}*A 令C=AT∗A 变 换 为 : A T ∗ A X = A T ∗ b 变换为:A^{T}*AX=A^{T}*b 变换为:AT∗AX=AT∗b 即 : C X = A T ∗ b = B 即:CX=A^{T}*b=B 即:CX=AT∗b=B
C 为 正 定 矩 阵 可 以 表 示 为 一 个 下 三 角 矩 阵 L 和 其 转 置 L T 的 积 : C为正定矩阵可以表示为一个下三角矩阵L和其转置L^{T}的积: C为正定矩阵可以表示为一个下三角矩阵L和其转置LT的积:
L ∗ L T X = B L*L^{T}X=B L∗LTX=B
令 : L T X = Y 、 先 通 过 L ∗ Y = B 求 得 Y , 再 通 过 L T X = Y 求 得 X 令:L^{T}X=Y 、 先通过 L*Y=B求得Y,再通过 L^{T}X=Y求得X 令:LTX=Y、先通过L∗Y=B求得Y,再通过LTX=Y求得X
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
sess = tf.Session()
A = np.linspace(0, 10, 100)
b = A + np.random.normal(0, 1, 100)
x_vals_column = np.transpose(np.matrix(A))
ones_column = np.transpose(np.matrix(np.repeat(1, 100)))
A = np.column_stack((x_vals_column, ones_column))
b = np.transpose(np.matrix(b))
A_tensor = tf.constant(A) #输入矩阵A
b_tensor = tf.constant(b) #输出矩阵B
tA_A = tf.matmul(tf.transpose(A_tensor), A_tensor) #求得正定矩阵C
L = tf.cholesky(tA_A) #三角矩阵L
tA_b = tf.matmul(tf.transpose(A_tensor), b)
sol1 = tf.matrix_solve(L, tA_b) #求得Y
sol2 = tf.matrix_solve(tf.transpose(L), sol1) #求得X
solution_eval = sess.run(sol2)
slope = solution_eval[0][0]
y_intercept = solution_eval[1][0]
print('slope: ' + str(slope))
print('y'_intercept: ' + str(y_intercept))
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Best' fit line',
linewidth=3)
plt.legend(loc='upper left')
plt.show()