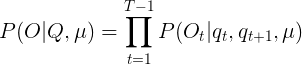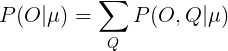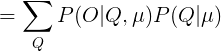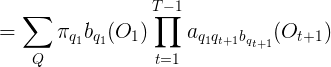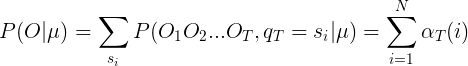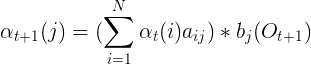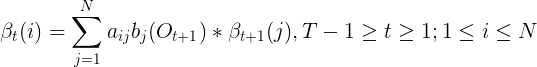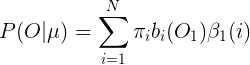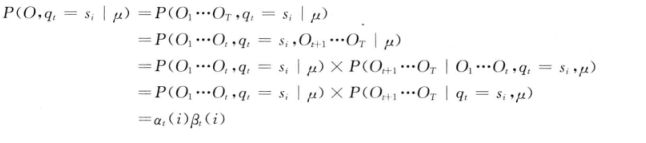NLP --- 隐马尔可夫HMM（第一个、第二个问题解决方案）

上一节我们详细的阐述了隐马尔可夫的三个基本问题，结合者背景知识理解这三个问题还是很容易的，因为隐马尔可夫的提出就是建立在语音识别的基础上提出来的，因此根据背景知识学习更容易吸收和深入理解，简单的来说就是物理意义，这里大家理解算法类的都尽量通过物理意义进行理解，这样学习效果会更好，另外就是本节只会解决前两个基本问题，结尾引出第三问题，然后分析问题的难点在哪里，讲明白为什么要引入EM算法，然后下一节将从最大释然估计讲解，由此引入EM算法，最后在解决第三个问题，废话不多说，下面开始：

隐马尔可夫的定义放在这里：

一般的，一个HMM记为一个五元组，其中，S为状态的集合，K为输出符号的集合，分别是初始状态的概率分布、状态转移概率和符号发射概率，为了简单，有时也将其记为三元组。详情解释请查看概念详解

第一个基本问题的解决方案

先把第一个基本问题拿过来看一下，没有深入理解的建议看我上一节的什么是三个基本问题（什么是三个基本问题）:

估计问题：给定一个观察序列和模型，如何快速地计算出给定模型情况下，观                                察序列的概率，即？

首先我们需要分析一下问题，给出的条件是观察序列和模型，让我们求在已知条件的情况下的条件概率即，上一节我们详细的阐述了这个问题是为了解决语音识别中的语音输入问题，即根据语料库计算出最有可能输入的语音（拼音）序列。下面我们就开始推公式了：

对任意的状态序列，有：

                                    

                                                                                            

这里解释一下，上式的表示在已知模型和状态序列的情况下求发射的符号序列的概率（HMM使用B表示符号发射概率），可以写成每个状态下发射符号O的概率的乘积，这里隐藏一个假设即不同的状态发射的符号是相互独立的，因此可以写成（1）式，我们继续：

                                                                                                

这里的表示的在已知模型的情况下求总状态转移的概率，HMM的定义状态转移概率使用A来表示，因此可以写成每个状态转移概率的乘积（这里马尔科夫链可得），继续往下：

                                                                                                 

上面的（3）式是根据（1）、（2）两式得来的，怎么解释他呢？意思是在模型的情况下的状态转移和发射符号序列的概率（这里是条件概率，O，Q是一体的），他就等于在模型的情况下的状态转移概率乘上即在和Q条件下的发射符号的概率，这里大家需要好好，体会，他们是不是相等的，

此时得到式后就好办了，是条件下的联合概率分布，那么我在条件的情况下也可以求边缘密度分布，因此就有下式：

                                          

                                                           

                                                           

上式大家应该很容理解了，分别带进去后就会得到上式，所以第一个问题最后就化简成上式了，那么我们如何求解呢？我们先看前一部分他是求和的，这部分的计算量不大，一旦转态转移Q确定下来基本上求和就确定下来了，难点在于后一部分的求积，既然要求最后的概率最大，那么就要求累乘的概率每转移到一个状态的概率达到最大，好，到这里我们再想想我们现在的目标是总体是概率最大，而上式的前一部分是求和，只要每个状态的转移和发射符号的概率最大那么求和的结果就会最大，后一部分要求转移概率的总乘积的概率最大，另外就是大家看看这里目标和算法中的哪个算法最类似？这里要求最大概率是针对全局概率，因此不能使用贪心算法，因为贪心算法只可能取得局部最优解，因此这里使用动态规划求解是最合适的，动态规划的算法这里不再详细解释了，年后我会专门开一个栏目讲算法的，这里我先简单的解释一下动态规划的核心思想，他是从结果分析，然后从结果（全局）出发，反推到开始，把结果都记录下来，然后写代码时通过递归直接调用计算好的结果，这里计算量就下来了，下面总体分析一下上式：

上述推导方式很直接，但面临一个很大的困难是，必须穷尽所有可能的状态序列。如果模型中有N个不同的状态，时间长度为T，那么，有NT个可能的状态序列。这样，计算量会出现“指数爆炸”。当T很大时，几乎不可能有效地执行这个算法。为此，人们提出了前向算法或前向计算过程（forward procedure)，利用动态规划的方法来解决这一问题，使“指数爆炸”问题可以在时间复杂度为的范围内解决。
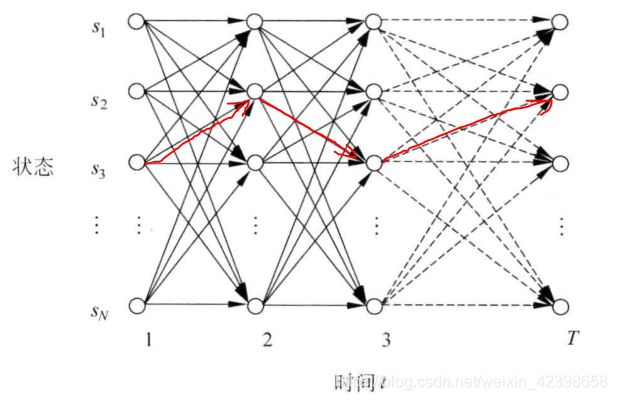
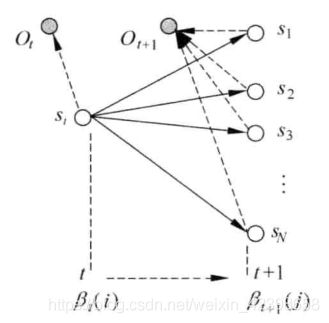
HMM中的动态规划问题一般用格架（trellis或lattice)的组织形式描述。对于一个在某一时间结束在一定状态的HMM，每一个格能够记录该HMM所有输出符号的概率，较长子路径的概率可以由较短子路径的概率计算出来，如下图：

这里解释一下上图是什么意思 ，首先表示状态，即隐马尔可夫总共有N个状态，每一个时刻的状态都是这里面的一种可能情况，因此上图的意思就是横向是时间走向1,2,3,4，，，，T，纵向就是每个时刻的可能选择的所有状态了，也就是说肯定存在一个通路是我们想要的，如上图的红线路径。因此从上图可以看出状态转移的可能输太多了，计算量很庞大，因此使用动态规划解决计算量大问题，使用递归去搜索全局最优解，下面是就是如何推出递归表达式呢？同时这个算法又叫前项算法。

前向算法

       为了找到递归的表达式或者说为了实现前项算法，这里需要定义一个中间变量（前项变量）即，如下定义：

        定义：  中间变量是在时间,HMM输出了序列，并且位于状态的概率：

                                  

前项算法的主要思想是，如果可以快速计算前项变量，那么就可以根据计算出是在所有状态下观察到序的概率：

                                   

所有说现在是如何构造这个递推关系式，这一点其实在算法中也是最难的即建模思想，这个需要你深入理解各个算法的优缺点的情况下，找出他们的递推关系，所以有时间的朋友还是把算法好好学一学，过段时间我也单独开开一系列总结算法。我们下面就分析如何找出他们的关系即和的关系，如果这一节你看不懂，或者理解困难，说明你对动态规划的算法理解的不深入，可以暂时停下来学习一下动态规划这个算法。下面开始推倒他们的关系：

在前项算法中，采用动态规划的方法计算前向变量，其实现思想基于如下：

在时间的前向变量可以根据在时间时的前向变量的值来归纳计算：

                                           

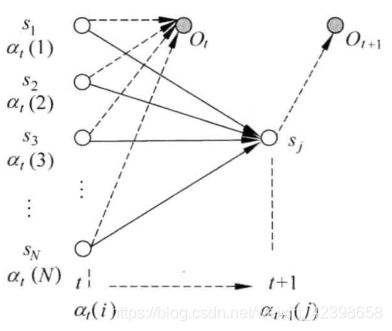
下面同示意图进行详细解释上式的意义：

上图代表的意思大家应该都懂吧，这里是时间t到t+1的转移过程，假设在t时刻的中间变量概率为，而表示在已知观察序列 的情况下，从时间到达下一个时间时的状态为的概率。从初始时间开始到，HMM到达状态，并输出观察序列的过程可以分解为一下两个步骤：

（1）从初始时间开始到时间，HMM到达状态，并输出观察序列；

（2）从状态转移到状态，并在状态输出。

这里的可以是HMM的状态集的任意一个状态，根据的定义，从某一个状态出发完成第一步的概率就是，而完成第二步的概率为。因此，从初始时间到这个过程的概率为。由于HMM可以从不同的转移到，一共有N个不同的状态，需要把能转移到这个状态的概率求和，这里大家可能会迷惑为什么是是在t时刻的求和呢？这里简单的解释一下，因为在t时刻的N种状态都有可能转移到，此时我们要求的是转移到的概率有多大，而在t时刻时我们已经分别知道了t-1时刻转移到t时刻的所有状态的概率，这就是从全局出发，即我不管t时刻从哪个状态转移到的概率，而是考虑总体上只关心t+1时刻在状态时的总概率是多少，这是动态规划的核心思想了。 因此就得到了上式的推倒。

因此通过上式可以以此计算，为HMM的状态变量，由此我们给出前项算法的伪代码：

    第一步    初始化：                    

    第二步   归纳计算：

                                                      

    第三步   求和结束：

                                                      

在初始化步骤中，是初始状态的概率，是在状态输出的概率，那么，就是在时刻t=1时，HMM在状态输出序列，即前项变量，一共有N个状态，因此需要初始化N个前项变量.

现在来分析一下前项算法的时间复杂性，由于每计算一个必须考虑时的所有N个状态转移到状态的可能性，其时间复杂性为，那么，对应每个时间t，要计算N个前项变量,因此时间复杂性为,因而，在1，2，。。。，T整个过程中，前项算法的总时间复杂性为

上面就是前项算法了，解决第一个基本问题还有另外一个方法就是后向算法，其实和前项算法很类似的，这里不细讲了，只把过程写一下。

后向算法

和前项算法类似，这里也定义一个前项变量.

     定义：后向变量是在给定了模型，并且在时间t状态为的条件下，HMM输出观察序列 的概率：
                                                         
与计算前向变量一样，可以用动态规划的算法计算后向变量。类似地，在时间t状态为的条件下，HMM输出观察序列的过程可以分解为以下两个步骤：
（1)  从时间t到时间，HMM由状态到状态,并从输出；

（2）在时间的状态为的条件下，HMM输出观察序列。
        第一步中输出的概率为：；

        第二步中根据后向变量的定义，HMM输出观察序列为的概率就是后向变量。于是，得到如下归纳关系：
                                                       
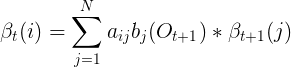
根据后向变量的归纳关系，按,顺序依次计算(x为HMM的状态），就可以得到整个观察序列.

伪代码：

    第一步    初始化：                   

    第二步   归纳计算：

                                                      

    第三步   求和结束：

                                                      

同理计算时间复杂度为也为。

还有一种算法是二者的结合，如下式：

以上就是解决第一个问题的算法了，下面介绍解决第二个问题的算法即维特比算法。

第二个基本问题的解决方案

这里也把第二个问题直接拿过来了，不懂的建议看我的上一篇博客：

序列问题：给定一个观察序列和模型：，如何快速有效地选择在一定意义下“最                             优”的状态序列，使得该状态序列“最好地解释”观察序列？

这里还是简单的通过语音识别的例子进行解释一下，其实简单来说就是我们输入了正确的语音信号（拼音），现在的问题是我们在已知模型和观察序列（拼音、语音信号）的情况下，去计算出对应的隐藏序列（汉字序列）使其最符合我们的观察序列。还不懂的看我的上一篇博客，别拖，别稀里糊涂。

维特比（Viterbi）算法用于求解HMM中的第二个问题，即给定一个观察序列和模型，如何快速有效地选择在一定意义下“最优”的状态序列使得该状态序列“最好地解释”观察序列。即在给定的模型和观察给定序列O的条件下，使的条件概率最大的状态序列，如下：

                                                       

所以如何求上式的最大概率呢？维特比算法使用了动态规划的搜索算法求解这种最优状态序列，为了实现这种搜索，首先定义一个维特比变量.

定义：  维特比变量在时间t时，HMM沿着某一条路径到达状态，并输出观察序列的最大概率：

                                                       

              与前向变量类似，有如下递归关系：

                                                        

这里我想还是解释一下上式，如果深入理解动态规划思想的朋友，上面的式子还是很简单的，因此这里，我还是来简单的解释一下吧，首先我们的目的是求最大概率的状态序列，而背景框架是和前向算法一样的 ，我们知道如果穷举，计算量太大了，而且这里的最大概率是全局最优的，因此最适合的就是动态规划算法了，动态规划算法的思想是从全局出发也就是从结果出发，这里的结果是 ，即最后一步的需要概率和最后一步以前的概率都是最大的，这样才能保证最后结果是最大的，然后最后一步是通过上一步过来的即上式了，那么要保证最后一步最大就要保证从上一步的状态转移到最后的状态的概率最大，这样不停寻找上一步就得出结果了。

这种递归关系使我们能够运用动态规划搜索技术。为了记录在时间t时，HMM通过哪一条概率最大的路径到达状态，维特比算法设置了另外一个变量用于路径记忆，让记录该路径上状态的前一个（在时间t-1的）状态。根据这种思路，给出如下维特比算法。     

维特比算法：

第一步          初始化：

                                                             

                                                               

第二步          归纳计算：

                                             

                                         记忆回退路径：

                                       

第三步            计算结束：

                                         

                                         

第四步             路径回溯：

                                               

维特比算法的时间复杂性与前向算法、后向算法的时间复杂性一样，也是。在实际应用中，往往不只是搜索一个最优状态序列，而是搜索n个最佳(n-best)路径，因此，在格架的每个结点上常常需要记录m个最佳（m-best，m

第三个问题：

           训练问题或参数估计问题：给定一个观察序列，如何根据最大似然估计来求模型的参数值？即如             何调节模型的参数，使得最大？   

首先这个问题很重要，而且解决起来也很困难，重要体现在他是构建模型的，因为我们的第一个问题和第二个问题都是建立在模型已知的情况下才能计算，所以这个问题的解决很重要，困难稍后解释。因此这个问题是最基础的问题，但是为什么要作为第三个问题呢？这是因为这个问题解决起来太麻烦了，因此这样安排。大家知道我们刚开始是没有模型的即HMM的参数都不知道，但是我们有什么呢？我们有语料，因为通过语料可以求解HMM的三个参数即状态转移概率A、符号发射概率B和初始状态概率分布。这里呢要想计算出这些参数，首先我们应该有完美的语料，如果没有完美的语料怎么办呢？所有我们从两方面进行探讨即有完美语料和没有完美语料。

完美语料

所谓完美语料就是我既知道发射符号的序列，也知道状态转移序列，这里我们就可以使用最大释然估计计算HMM的参数了，下面通过书面语进行说明：

参数估计问题是HMM面临的第三个问题，即给定一个观察序列，如何调节模型的参数，使得最大化：
                                                
模型的参数是指构成的。最大似然估计方法可以作为HMM参数估计的一种选择。如果产生观察序列的状态序列已知，根据最大似然估计，HMM的参数可以通过如下公式计算：

                                                  

上面的是冲击函数即当两个参数相等是为1，反之为0

不完美语料

不完美语料是指知道观察序列但是不知道状态转移序列，因此无法用最大释然估计进行解决，此时可以是使用EM 算法【Expectation Maximization（期望最大化）】，到这里本节就结束了，下一节将从最大释然估计开始，然后讲EM算法，最后再讲三个问题的具体解决过程。

 

注：本节主要参考了宗成庆的《统计自然语言处理》