推荐系统-node2vec 技术在设计网络推荐中的应用

美国著名的第三方调查机构尼尔森调查了影响用户相信某个推荐的因素，调查结果显示，9 成的用户相信朋友对他们的推荐，7 成的用户相信网上其他用户对广告商品的评论。从该调查可以看到，好友的推荐对于增加用户对推荐结果的信任度非常重要。

因此，在社交网络的背景下，推荐系统不单单需要关注用户与物品之间的关系，还要关注用户之间的关系。

在社交网站方面，国外以 Fackbook 和 Twitter 为代表，国内社交网站以新浪微博、QQ 空间等为代表。这些社交网站形成了两类社交网络结构。

【社交网络结构】：

• 社交图谱：好友一般是自己在现实社会中认识的人，比如同事、同学、亲戚等，并且这种好友关系是需要双方确认的，如 Fackbook、QQ 空间。
• 兴趣图谱：好友往往都是现实中互不相识的，只是出于对对方言论的兴趣而建立好友关系，并且这种好友关系也是单向的关注关系，如 Twitter、新浪微博。

需要注意的是，任何一个社会化网站都不是单纯的社交图谱或兴趣图谱。在 QQ 空间中大多数用户联系基于社交图谱，而在微博上大多数用户联系基于兴趣图谱。但在微博中，也会关注现实中的亲朋好友，在 QQ 中也会和部分好友有共同兴趣。

在社交网络中需要表示用户之间的联系，可以用图 G(V, E, W) 定义一个社交网络。其中 V 是顶点集合，每个顶点代表一个用户，E 是边集合，如果用户 $V_a$ 和 $V_b$ 有社交网络关系，那么就有一条边 $e(V_a,V_b)$ 连接这两个用户，$W(V_a,V_b)$ 用来定义边的权重。

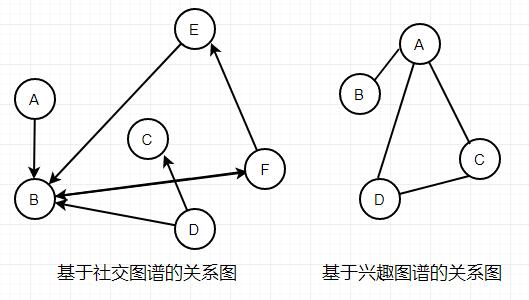
• 社交图谱：朋友关系是需要双向确认的，因而可以用无向边连接有社交网络关系的用户——无向图；
• 兴趣图谱：朋友关系是单向的，可以用有向边代表这种社交网络上的用户关系——有向图。

在之前的博客[推荐系统-基于用户的推荐在社交网络中的应用]中，(https://blog.csdn.net/weixin_43378396/article/details/91129814)我们使用了基于用户社交网络计算用户相似度的方法，但对于新浪微博、微信这样大规模的社交关系，离线计算好用户的相似度并存储下来供线上推荐系统使用，显然不合理。那能否用一个坐标表示来描述用户在社交网络中的位置呢？这样只需提前计算好用户坐标，线上计算用户之间的相似度时，只要计算坐标的距离或者余弦相似度即可。node2vec 可以帮助我们实现这个目标。

【node2vec 整体思路】：

1. random walk（随机游走），通过一定规则随机抽取一些点的序列。
2. 将点的序列输入至 Word2Vec 模型，从而得到每个点的 embedding 向量。

下面我们将分别介绍这两个步骤的计算方法。

random walk

【基本流程】：给定一张图 G 和一个起始节点 S，标记起始节点位置为当前位置，随机选择当前位置节点的一个邻居，并将当前位置移动至被选择的邻居位置，重复以上步骤 n 次，最终会得到从初始节点到结束节点的一条长度为 n 的“点序列”，此条“点序列”即称为在图 G 上的一次 random walk。

【示例】：假设我们的起始节点为 A，随机游走步数为 4。

• 首先从 A 开始，有 B、E 两个节点可游走，我们随机选择 B；
• 再从 B 开始，有 A、E、F 三个备选下一节点，随机选择节点为 F；
• 再从 F 开始，于 B、C、D、E 四个节点，我们随机选取 C；
• 再从 C 开始，游走到 H。
• 达到游走步数，停止随机游走。我们获得一条 random walk 路径：A -> B -> F -> C -> H。

由上面的实例可以看出，random walk 算法主要分为两步：

1. 选择起始节点：起始节点的选择存在两种常见的做法。
   1. 按照一定规则随机从图中抽取一定数量的节点；
   2. 以图中所有节点作为起始节点。一般来说我们选择这种方式，以便所有节点都能被选取到。
2. 选择下一节点：最简单方法是按照边的权重随机选择，但是在实际应用中，我们希望能控制广度优先还是深度优先，从而影响 random walk 能够游走到的范围。
   • 深度优先：发现能力更强；
   • 广度优先：社区内的节点更容易出现在一个路径中。

斯坦福大学计算机教授 Jure Leskovec 给出了一种可以控制广度优先或者深度优先的方法。

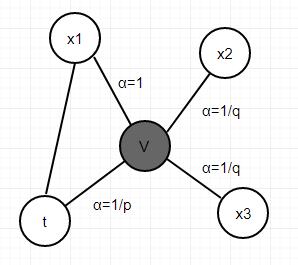
以上图为例，我们假设第一步是从 t 随机游走到 v，接下来要确定下一步的邻接节点。参数 p 和 q 用以调整游走节点的倾向。

• p：计算回到上一节点的概率；
• q：计算走到远离上一节点的节点概率。

首先计算当前节点的邻居节点与上一节点 t 的距离 d，根据公式可得 α。
$$\alpha =\{\begin{array}{l}1/p,d=0\\ 1,d=1\\ 1/q,d=2\end{array}$$

根据 α 的值确定下一节点的选择概率。

• 如果 p 大于 max(q, 1)，那么 1/p 小于 1/q，则产生的序列与深度优先类似，刚刚被访问过的节点不太可能被重复访问。
• 如果 p 小于 min(q, 1)，那么 1/p 大于 1/q，则产生的序列与广度优先搜索类似，倾向于周边节点。

至此，我们就可以通过 random walk 生成点的序列样本。一般来说，我们会从每个点开始游走 5~10 次，步长则根据点的数量 N 游走 $\sqrt{N}$。

代码实现

首先，引入所需的包以及数据。

>>> import numpy as np
>>> import pandas as pd
>>> focus = pd.read_csv('data/focus.csv')
>>> focus
userId	focus
0	A	B
1	B	F
2	D	B
3	D	C
4	E	B
5	F	B
6	F	E
>>> focus_dataset = focus.values
>>> focus_dataset
array([['A', 'B'],
       ['B', 'F'],
       ['D', 'B'],
       ['D', 'C'],
       ['E', 'B'],
       ['F', 'B'],
       ['F', 'E']], dtype=object)

接着，根据数据集建立邻接表。

class Node(object):
    
    def __init__(self, val):
        self.value = val
        self.neighbors = {}
        
    def __str__(self):
        return self.value
        

def build_neighbors_table(dataset):
    header_table = {}
    for data in dataset:
        user, focus = data[0], data[1]
        if user not in header_table:
            node_user = Node(user)
            header_table[user] = Node(user)
        if focus not in header_table:
            node_focus = Node(focus)
            header_table[focus] = node_focus
        header_table[user].neighbors[focus] = header_table[focus]
    return header_table

【说明】：build_neighbors_table() 函数接受数据集，并生成邻接表。

• 初始化头指针字典，然后遍历数据集，在每一轮迭代中获取用户以及关注用户信息；

header_table = {}
for data in dataset:
    user, focus = data[0], data[1]

• 判断用户以及关注用户是否在 header_table 中，若不存在，则创建该用户节点，并添加到 header_table 中。

if user not in header_table:
    node_user = Node(user)
    header_table[user] = Node(user)
if focus not in header_table:
    node_focus = Node(focus)
    header_table[focus] = node_focus

• 根据关注关系，建立用户节点间的联系。

header_table[user].neighbors[focus] = header_table[focus]

然后，实现 random walk 算法。由于该算法涉及到的步骤较多，将其拆分为 random_choose() 以及 random_walk() 两部分。先来看 random_choose() 函数的实现。

def random_choose(neighbors, node_cur, node_last, p, q):
    # 如果上个节点为 None,则随机选择一个节点
    if node_last is None:
        random = int(np.ceil(np.random.random() * len(node_cur.neighbors)))
        ind = 1
        for node_user in neighbors:
            if ind == random:
                return neighbors[node_user]
            ind += 1
    # 否则，计算通往各节点的权重，并根据权重选择下一节点
    prob = {}
    for node_user in neighbors:
        node = neighbors[node_user]
        if node == node_last:
            prob[node] = 1 / p
        elif node in node_last.neighbors or node_last in node.neighbors:
            prob[node] = 1
        else:
            prob[node] = 1 / q
    
    total = 0
    for key in prob:
        total += prob[key]
    random = np.random.random() * total
    total_prob = 0
    for key in prob:
        total_prob += prob[key]
        if total_prob > random:
            return key

【说明】：random_choose() 函数接受五个参数，当前节点的邻居节点 neighbors、当前节点 node_cur，上一个节点 node_last、调节搜索方式的 p 和 q。

• 首先判断 node_last 是否为 None（实际上判断当前节点是否为起始点），若为 None，则随机从邻居节点中挑选一个。

if node_last is None:
    random = int(np.ceil(np.random.random() * len(node_cur.neighbors)))
    ind = 1
    for node_user in neighbors:
        if ind == random:
            return neighbors[node_user]
        ind += 1

• 如果 node_last 不为 None，则根据公式计算通往各邻居节点的权重。

prob = {}
for node_user in neighbors:
    node = neighbors[node_user]
    if node == node_last:
        prob[node] = 1 / p
    elif node in node_last.neighbors or node_last in node.neighbors:
        prob[node] = 1
    else:
        prob[node] = 1 / q

• 最后，根据各邻居节点的权重选择下一节点。

total = 0
for key in prob:
    total += prob[key]
random = np.random.random() * total
total_prob = 0
for key in prob:
    total_prob += prob[key]
    if total_prob > random:
        return key

再来看 random_walk 函数的实现。

def random_walk(header_table, iter_count=1, step=5, back=0.5, forward=0.7): 
    path = []
    for user in header_table:
        for i in range(iter_count):
            node_last = None
            node_cur = header_table[user]
            path_iter = [node_cur.value]
            for j in range(step):
                neighbors = node_cur.neighbors
                # 若已“无路可走”则退出循环
                if len(neighbors) == 0:
                    break
                node_next = random_choose(neighbors, node_cur, node_last, back, forward)
                path_iter.append(node_next.value)
                node_last = node_cur
                node_cur = node_next
            path.append(path_iter)
    return path

【说明】：random_walk() 函数接受五个参数，头指针字典 header_table，游走次数 iter_count，步长 step 以及回退参数 back（p）和前进参数 forward（q）。

• 依次将各节点作为起始点，并且每个节点游走 iter_count 次。每次游走时进行初始化操作，将 node_last 设置为 None，node_cur 设置为当前节点，用以存储游走路径的 path_iter 列表默认存储当前节点。

path = []
for user in header_table:
    for i in range(iter_count):
        node_last = None
        node_cur = header_table[user]
        path_iter = [node_cur.value]
        # ...

• 然后，根据步长参数不断循环，每到一个节点先获取当前节点的邻居节点，若邻居节点不存在，则跳出循环。

for j in range(step):
    neighbors = node_cur.neighbors
    # 若已“无路可走”则退出循环
    if len(neighbors) == 0:
        break
    # ...

• 接着，调用 random_choose() 函数选择下一个节点，并将下一个节点的值存储到 path_iter 列表中，并更新 node_last、node_cur 的值，以实现节点的“跳动”。

node_next = random_choose(neighbors, node_cur, node_last, back, forward)
path_iter.append(node_next.value)
node_last = node_cur
node_cur = node_next

• 最后，将所有的路径保存到总路径 path 列表中，并返回。

        path.append(path_iter)
return path

【代码测试】：

>>> path = random_walk(header_table, iter_count=2, step=3)
>>> path
[['A', 'B', 'F', 'E'],
 ['A', 'B', 'F', 'E'],
 ['B', 'F', 'E', 'B'],
 ['B', 'F', 'E', 'B'],
 ['F', 'E', 'B', 'F'],
 ['F', 'B', 'F', 'B'],
 ['D', 'C'],
 ['D', 'B', 'F', 'E'],
 ['C'],
 ['C'],
 ['E', 'B', 'F', 'B'],
 ['E', 'B', 'F', 'B']]

能够看到每个节点都作为起始点参与 random walk，且游走了两次，步长为 3。

Word2Vec

在上一步中，我们已经获得了点的序列样本，那么下一步需要解决的问题是：如何根据点序列生成每个点的特征向量，即我们先前提到的“用户坐标”。

Word2Vec 可以解决这个问题，Word2Vec 是从大量文本语料中以无监督的方式学习语义知识的一种模型，它的核心目标是通过一个嵌入空间将每个词映射到一个空间向量上，并且使得语义上相似的单词在该空间内距离很近。关于 Wrod2Vec 模型可参考 test

实际上 random walk 算法获得的用户节点序列，每一个节点其实对应了 Word2Vec 中的单词，模型的输入是某个用户的 one-hot 编码，输出是该用户在节点序列前后的节点，例如输入是 F 的编码，输出是 A、B、C、D 的概率分布。最后得到的输出是每个节点（即用户）的 Word2Vec 向量。

有了数值化的向量，对于任意两个用户，我们就可以通过余弦距离或霍式距离来计算这两个用户的相似度。

【代码实现】：

from gensim.models import Word2Vec


path = random_walk(header_table, iter_count=2, step=3)
model = Word2Vec(path, min_count=2)

def choose_similarity_user(self, user, user_list, user_num):
    similarity_user = []
    for user_ in user_list:
        if user != user_:
            similarity_user.append((user_, self.model_.wv.similarity(user, user_)))
    eturn sorted(similarity_user, key=lambda x:x[1], reverse=True)[:user_num]

我们可以直接把 random_walk() 生成的 path 列表直接掉 Word2Vec() 中，让其进行训练。

接下来我们只需要依次判断 user_list 中的用户与当前用户的相似度，从中挑选相似度最高的 user_num 用户。

【完整代码】：可从 GitHub 中获得 传送门

参考

• 《推荐系统与深度学习》