二叉树三种遍历的递归和迭代实现

本文所有代码都在leetcode上提交成功，所以输入输出的格式与leetcode上题目一致，下面分析三种遍历使用到的二叉树如下图所示：

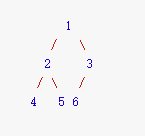
中序遍历

该二叉树的中序遍历为{4,2,5,1,6,3}。

递归实现

分析上面中序遍历后的序列，可以发现上面的中序遍历序列可以划分为{{4,2,5},1,{6,3}}，可以看出中序遍历的结果可以按如下方法生成：
1.中序遍历左子树
2.输出根节点的值
3.中序遍历右子树
因此，中序遍历的递归代码如下：

 //leetcode的接口函数
 vector inorderTraversal(TreeNode* root) {
     vector result;
     traversal(root,result);
     return result;
 }
 //具体实现的函数
 void traversal(TreeNode* root,vector& result){
     if(root != NULL){
         traversal(root->left,result);
         result.push_back(root->val);
         traversal(root->right,result);
     }
     else
         return;
 }

迭代实现

   首先，我们访问二叉树节点只能从根节点出发，但是中序遍历是从最左边的  
叶节点开始遍历的，所以我们肯定需要一个先进后出的数据结构来保存从根节点  
开始访问时的二叉树上层的节点(上层节点是相对于叶节点而言的)，因此我们  
使用栈来保存访问到叶子节点之前的节点。
   然后，由于是从最左边的叶子节点开始的，所以需要一直将左孩子弹入栈直
至左孩子为空。此时开始出栈，弹出一个节点后，需要将该节点的右子树以相
同的方式入栈。
   最后，直到栈为空，并且当前节点也为空了，说明遍历完成。

迭代的思路总结如下：
初始情况下，根节点为当前节点，栈为空
1.将当前节点的左孩子全部入栈
2.弹出栈顶元素，出栈时保存该元素的值，将当前节点替换为栈顶节点的右孩子
3.如果当前节点为空并且栈中元素全部弹出(即栈为空)则结束循环，否则转到第1步
思考为什么是并且？

vector inorderTraversal(TreeNode* root) {
    vector result;
    stack tmp;
    if(root == NULL)
        return result;
    while(root != NULL || !tmp.empty()){
        while(root != NULL){
            tmp.push(root);
            root = root->left;
        }
        if(!tmp.empty()){
            root = tmp.top();
            tmp.pop();
            result.push_back(root->val);
            root = root->right;
        }
    }
    return result; 
}

上面的代码执行的过程中，对于示例的二叉树，栈里的元素变化如下：
{}弹入{1,2,4}
{1,2,4}弹出4，不弹入
{1,2}弹出2 ，弹入{5}
{1,5}弹出5，不弹入
{1}弹出1，弹入{3,6}
{3,6}弹出6，不弹入
{3}弹出3，不弹入
{}结束

前序遍历

该二叉树的前序遍历为{1,2,4,5,3,6}。

递归实现

分析上面前序遍历后的序列，可以发现上面的前序遍历序列可以划分为{1,{2,4,5},{3,6}}，可以看出中序遍历的结果可以按如下方法生成：
1.输出根节点的值
2.前序遍历左子树
3.前序遍历右子树
因此，前序遍历的递归代码如下：

 //leetcode的接口函数
 vector preorderTraversal(TreeNode* root) {
        vector result;
        helper(root,result);
        return result;
  }
 //具体实现的函数
 void helper(TreeNode* root, vector& result){
     if(root != NULL){
         result.push_back(root->val);
         helper(root->left,result);
         helper(root->right,result);
     }
     else
         return;
 }

迭代实现1

仔细思考，前序遍历的迭代代码只需要对中序遍历的迭代代码进行一点点更改就可以了，那就是在入栈的时候保存元素的值就可以了(本质是因为前序遍历是从根节点开始的，所以这给入栈时保存元素来完成遍历提供了可能性，中序遍历就无法通过入栈时保存元素来完成遍历)。
迭代的思路总结如下：
初始情况下，根节点为当前节点，栈为空
1.将当前节点的左孩子全部入栈，入栈时保存该元素的值
2.弹出栈顶元素，将当前节点替换为栈顶节点的右孩子
3.如果当前节点为空并且栈中元素全部弹出(即栈为空)则结束循环，否则转到第1步

vector preorderTraversal(TreeNode* root) {
    vector result;
    stack tmp;
    if(root == NULL)
        return result;
    while(root != NULL || !tmp.empty()){
        while(root != NULL){
            result.push_back(root->val);
            tmp.push(root);
            root = root->left;
        }
        if(!tmp.empty()){
            root = tmp.top();
            tmp.pop();
            root = root->right;
        }
    }
    return result; 
}

迭代实现2

第一种迭代方法是在入栈时保存元素来完成遍历，那么有没有出栈时保存元素来完成遍历呢？答案是有的，实现思路如下：
初始情况下，弹入根节点
1.弹出栈顶元素，出栈时保存该元素的值
2.将当前节点替换为弹出的节点，如果当前节点的右节点不为空，弹入右节点；如果当前节点的左节点不为空，弹入左节点
3.如果栈为空，结束循环，否则转到第1步
思考判断当前节点的两个孩子节点是否为空时为什么是先右后左？

vector preorderTraversal(TreeNode* root) {
    vector result;
    stack tmp;
    if(root == NULL)
        return result;
    else{
        tmp.push(root);
        while(!tmp.empty()){
            root = tmp.top();
            tmp.pop();
            result.push_back(root->val);
            if(root->right != NULL){
               tmp.push(root->right); 
            }
            if(root->left != NULL){
                 tmp.push(root->left);
            }               
        }
    }
    return result;
}

上面的代码执行的过程中，对于示例的二叉树，栈里的元素变化如下：
{}，弹入1
{1}弹出1，弹入{3,2}
{3,2}弹出2，弹入{5,4}
{3,5,4}弹出4，不弹入
{3,5}弹出5，不弹入
{3}弹出3，弹入{6}
{6}弹出6，不弹入
{}结束

后序遍历

该二叉树的后序遍历为{4,5,2,6,3,1}。

递归实现

分析上面后序遍历后的序列，可以发现上面的后序遍历序列可以划分为{{4,5,2},{6,3},1}，可以看出中序遍历的结果可以按如下方法生成：
1.后序遍历左子树
2.后序遍历右子树
3.输出根节点的值
因此，后序遍历的递归代码如下：

//leetcode的接口函数
vector postorderTraversal(TreeNode* root) {
   vector result;
   helper(root,result);
   return result;
}
//具体实现的函数
void helper(TreeNode* root,vector& result){
   if(root != NULL){
       helper(root->left,result);
       helper(root->right,result);
       result.push_back(root->val);
   }
   else
       return;
}

迭代实现1

仔细观察，不难发现，如果在前序遍历的时候，往栈里面弹入元素的顺序是先左后右，那么得到的序列刚好是后序遍历的反序列，那么此时只需将这个反序列反转一下就可以得到后序遍历的序列
(前序遍历是根节点->左子树->右子树，颠倒入栈顺序后为根节点->右子树->左子树，刚好与后序遍历左子树->右子树->根节点的顺序是相反的）
实现思路如下：
使用一个栈初始情况下，弹入根节点
1.弹出栈顶元素，出栈时保存该元素的值(不直接保存在结果里，而是先弹入一个栈中)
2.将当前节点替换为弹出的节点，如果当前节点的左节点不为空，弹入左节点；如果当前节点的右节点不为空，弹入右节点
3.如果栈为空，结束循环，否则转到第1步
最后反转一下栈中的序列即可(由于栈本身的特性，直接从顶部一直弹出即可完成反转)

vector postorderTraversal(TreeNode* root) {
    vector result;
    stack tmp;
    stack tmp2;         //用于反转序列的栈
    if(root == NULL)
        return result;
    else{
        tmp.push(root);
        while(!tmp.empty()){
            root = tmp.top();
            tmp.pop();
            tmp2.push(root->val);
            if(root->left != NULL){
                tmp.push(root->left);
            }
            if(root->right != NULL){
                tmp.push(root->right);
            } 
        }
    }
    //反转序列
    while(!tmp2.empty()){
        result.push_back(tmp2.top());
        tmp2.pop();          
    }
    return result;
}

迭代实现2

还有一种比较复杂的思路，在中序遍历的基础上，加上对于右子树的 一个标记来完成后序遍历
迭代的思路总结如下：
初始情况下，根节点为当前节点，栈为空
1.将当前节点的左孩子全部入栈
2.替换当前节点为栈顶元素。如果当前节点的右子树为空或者已经被遍历过，那么弹出栈顶元素，出栈时保存该元素的值，否则将根节点替换为栈顶节点的右孩子
3.如果当前节点为空并且栈中元素全部弹出(即栈为空)则结束循环，否则转到第1步

vector postorderTraversal(TreeNode* root) {
    vector result;
    stack tmp;
    TreeNode* cur;
    TreeNode* last = NULL;
    while(root != NULL || !tmp.empty()){
        while(root != NULL){
            tmp.push(root);
            root = root->left;
        }
        cur = tmp.top();
        //如果右子树为空或者右子树已经遍历过，那么就弹出这个节点，否则把该节点的右子树按照上面的依次将其左孩子入栈
        if(cur->right == NULL || cur->right == last){
            tmp.pop();
            result.push_back(cur->val);
            last = cur;
        }
        else{
            root = cur->right;
        }
    }
    return result;
}