决策树
1、三种树及特征：
1）ID3：信息增益法选择特征， 只能用于分类预测，生成的是多叉树，不能处理连续特征，不支持剪枝
2）C4.5：信息增益比选择特征， 只能用于分类预测，生成多叉树，可以处理连续特征，支持剪枝
3）CART:可用于分类预测（Gini系数）和回归预测（均方差），可以处理连续特征，生成二叉树，支持剪枝
2、两大问题：
2.1 树的生长，即利用训练样本集完成决策树的建立过程。
一般过程：
前提：对于样本集S，特征集F，样本输出集合Y
1、设置特征选择方法（如信息增益或信息增益比或Gini）的阈值z
2、判断样本中的类别是否都是同一类别，若是，停止递归，以该类别作为叶子节点
3、判断样本中特征集合是否为空，若是，停止递归，以样本输出类别的取值中，类别概率最高的类别作为叶子节点
4、计算各特征的信息增益（或者信息增益比）（针对ID3或C4.5）或者计算各特征的各类别取值的Gini系数（对于CART），选出使信息增益（或信息增益比）最大的特征Fk,或者选出Gini最小的特征及对应的特征取值
5、若信息增益（比）或Gini小于阈值z，则停止递归，以样本输出类别的取值中，类别概率最高的类别作为叶子节点
6、对于ID3或C4.5： 以该特征不同类别取值的不同输出类别Yi划分子节点，计算此时的子节点数T；对于CART，对该特征进行二分
7、Y<-Yi, 对于ID3或C4.5:F<-F-Fk, 对于CATR，由于对特征进行二分，若该特征取值未完全分开，后续该特征还会参与子节点选择。
8、重复2~7
2.2 树的剪枝，即利用测试样本集对所形成的决策树进行精简
- 预修剪: 通过指定树的最大深度、节点所含最小样本量来阻止树的充分生长
- 后修剪：先允许树充分生长，再指定一个允许的最大预测误差值，当决策树在测试样本集上的错误率明显增大时，应停止剪枝
2.2.1 最小代价复杂度剪枝法
R（T）：在测试样本集上的预测误差(错判率或均方误差)
｜ T ｜：T的叶节点数目；
α：复杂度参数
若中间节点的代价复杂度大于它的子树代价复杂度，否则应该保留子树。否则应该剪掉子树（Tt为子树叶子节点）
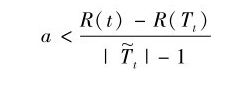
2.2.2 N倍交叉验证剪枝
- 模型选择：通过不断调整N的取值，找到在预测误差最小下的N值。该N值下的模型（参数）应是一个最佳模型。
- N个预测模型，得到N个在测试样本集上的预测误差。N个预测误差的平均值，作为模型真实预测误差的估计。
2.4 算法：CART、C4.5、C5.0（后2种是对ID3算法的延伸）
3.决策树的应用及剪枝
3.1仍以992年美国总统选举的数据分析不同背景人群的倾向：
变量包含：总统候选人、年龄、年龄分类、受教育年限、最高学历、性别 。
导入数据，设置参数，进行初步建树（先令cp=0建立充分生长的树）
数据概览：
library(rpart)
library(rpart.plot)
library(rattle)
library(readxl)
df <- read_excel('voter.xlsx',sheet = 1)
head(df)
dim(df)
str(df)
#分类变量转换为因子
df$pres92 = as.factor(df$pres92)
df$agecat = as.factor(df$agecat)
df$educ = as.factor(df$educ)
df$degree = as.factor(df$degree)
df$sex = as.factor(df$sex)
#建立分类树，异质性测度标准为信息增益
rc <- rpart.control(minsplit=10, xval=10, maxdepth=30,cp=0)
myTree <- rpart(pres92~age+educ+degree+sex, data=df, method='class',parms=list(split='information'), control=rc)
查看此时的树，很显然非常茂盛
rpart.plot(myTree,type=1,extra=3,branch=1)
查看树建立过程中cp的变化及交叉验证预测误差
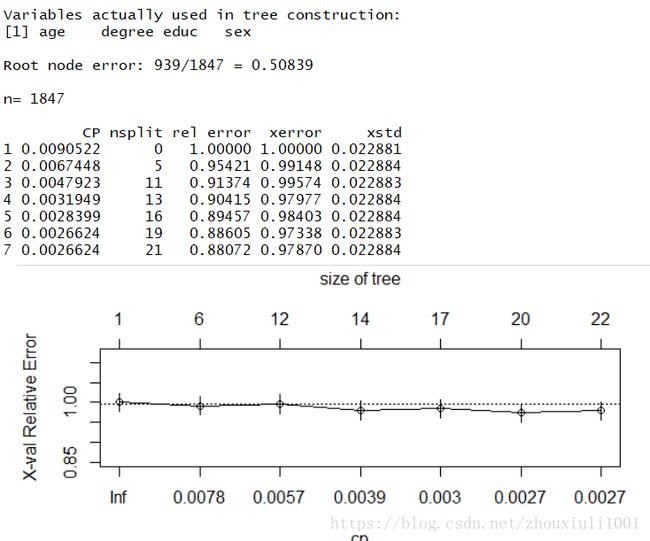
printcp(myTree)
plotcp(myTree)
参数理解：
cp:复杂度，nsplit:样本分组次数，rel error:是预测误差相对值的估计
xerror:交叉验证的预测误差相对值(相对于根节点)，xstd:预测误差的标准误
本样本共有观测1847，根节点错判率939/1847 = 0.50839为单位1，可见，经过19次分组（产生20个叶子节点）交叉验证误差最小为0.97*0.50839=0.493。
下面对树进行剪枝，将复杂度cp设为19次分组时的cp=0.00266
#树的剪枝
treeFit <- prune(myTree, cp=0.00266)
rpart.plot(treeFit,type=1,extra=3,branch=1)
printcp(treeFit)
plotcp(treeFit)
得到如下的树
参数如下，可知经过19次分组的预测错误率是最低为49%
换一种方式显示树结构，会清晰点：
plot(treeFit, uniform = T, branch = 0.8, margin = 0.1, main = "Tree Classification", compress = T)
text(treeFit, use.n = T, cex = 0.9)
还可以生成规则
asRules(treeFit)
规则解释：以第一个为例：有22个满足条件（
age>=48.5
educ=11,12,13,14,15,16,17,18,20
sex=1
educ=14,15,16,17,18
age>=62.5
educ=14,16）被预测为类别1（pres92=1），错判率为50%
以上述模型对样本所有观测进行预测，查看各分类错判率：
t1 <- diag(tb1)
rs <-vector()
for(i in 1:3){
a = 1-t1[i]/sum(tb1[,i])
rs = c(rs,a)
};rs
第1类的错判率为0.4962217，第2类为0.2380952，第3类为0.4464661
