20200401零基础入门数据挖掘 - 二手车交易价格预测笔记（4）

四、建模与调参

4.1 线性回归模型：

• 线性回归对于特征的要求；
• 处理长尾分布；
• 理解线性回归模型；

4.2 模型性能验证：

• 评价函数与目标函数；
• 交叉验证方法；
• 留一验证方法；
• 针对时间序列问题的验证；
• 绘制学习率曲线；
• 绘制验证曲线；

4.3 嵌入式特征选择：

• Lasso回归；
• Ridge回归；
• 决策树；

4.4 模型对比：

• 常用线性模型；
• 常用非线性模型；

4.5 模型调参：

• 贪心调参方法；
• 网格调参方法；
• 贝叶斯调参方法；

下面节选一些我学习比较多的地方进行记录：

4.1.1 线性回归

1. 建立线性模型

from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize=True)
model = model.fit(train_X, train_y)

并通过以下代码去查看线性回归模型的截距与权重：

'intercept:'+ str(model.intercept_)

sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)

2. 要注意线性回归有五个基本假设

• 线性性&可加性：

假设因变量为Y，自变量为X₁，X₂，则回归分析的默认假设为Y=b+a₁X₁+a2X₂+ε。
线性性：X₁每变动一个单位，Y相应变动a₁个单位，与X₁的绝对数值大小无关。
可加性：X₁对Y的影响是独立于其他自变量(如X2)的。
若事实上变量之间的关系不满足线性性（如含有X₁², X₁³ 项），或不满足可加性（如含有X₁⋅X₂项），则模型将无法很好的描述变量之间的关系，极有可能导致很大的泛化误差。

• 误差项(ε)之间应相互独立。

自相关性经常发生于时间序列数据集上，后项会受到前项的影响。当自相关性发生的时候，我们测得的标准差往往会偏小，进而会导致置信区间变窄。

• 自变量(X₁，X₂)之间应相互独立。

如果我们发现本应相互独立的自变量们出现了一定程度（甚至高度）的相关性，那我们就很难得知自变量与因变量之间真正的关系了。当多重共线性性出现的时候，变量之间的联动关系会导致我们测得的标准差偏大，置信区间变宽。

• 误差项（ε）的方差应为常数。

异方差性的出现意味着误差项的方差不恒定，这常常出现在有异常值（Outlier）的数据集上，如果使用标准的回归模型，这些异常值的重要性往往被高估。在这种情况下，标准差和置信区间不一定会变大还是变小。

• 误差项（ε）应呈正态分布。

如果误差项不呈正态分布，意味着置信区间会变得很不稳定，我们往往需要重点关注一些异常的点（误差较大但出现频率较高），来得到更好的模型。

3. 绘制特征v_9的值与标签的散点图，这里选择v_9作图可能是因为前面看权重的时候发现v_9的coef为正且值很大。

from matplotlib import pyplot as plt
subsample_index = np.random.randint(low=0, high=len(train_y), size=50)

由图可知，模型的预测结果（蓝色点）与真实标签（黑色点）的分布差异较大，且部分预测值出现了小于0的情况，从而判断模型存在一定的问题。又做了数据标签(price)的图可见其呈现长尾分布，违反了误差项应属于正态分布这一假设。

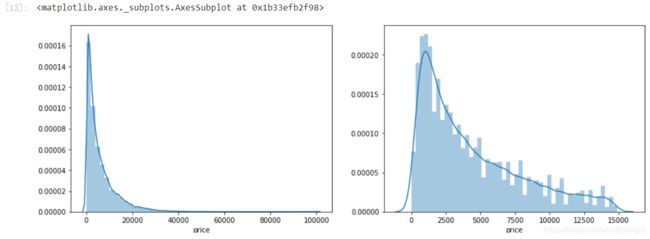
TIP: 这里学习手册中使用了$log(x+1)$的方式进行变换，从而让该分布贴近正态分布，是我之前不知道的调整方式，值得学习。

train_y_ln = np.log(train_y + 1)
import seaborn as sns
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y_ln)
plt.subplot(1,2,2)
sns.distplot(train_y_ln[train_y_ln < np.quantile(train_y_ln, 0.9)])

经过这一步骤再作出v_9的值与标签的散点图会得到预测结果与真实值较为接近，也没有过多的小于0的情况。

4.2.1 交叉验证

k折交叉验证：是用于模型调优的一种方式，测试时不把所有的数据集都拿来训练，分出一部分数据集来（这一部分不参加训练）对训练集生成的参数进行测试，找到使得模型泛化性能最优的超参值。每次迭代过程中每个样本点只有一次被划入训练集或测试集的机会。

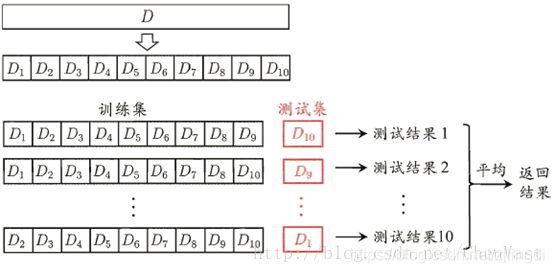
如果训练数据集相对较小，则增大k值。如果训练集相对较大，则减小k值。

from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error,  make_scorer
def log_transfer(func):
    def wrapper(y, yhat):
        result = func(np.log(y), np.nan_to_num(np.log(yhat)))
        return result
    return wrapper
scores = cross_val_score(model, X=train_X, y=train_y, verbose=1, cv = 5, scoring=make_scorer(log_transfer(mean_absolute_error)))

4.5.1 模型调参

1. 贪心算法：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，它所做出的仅仅是在某种意义上的局部最优解。采用的贪心策略一定要仔细分析其是否满足无后效性（即某个状态以后的过程不会影响以前的状态，只与当前状态有关）。
2. GridSearchCV：当算法模型效果不是很好时，可以通过该方法来调整参数，尝试每一种参数组合，返回最好的得分值的参数组合。每个参数都能组合在一起，循环过程就像是在网格中遍历，所以叫网格搜索。
3. 贝叶斯调参：贝叶斯优化通过基于目标函数的过去评估结果建立替代函数（概率模型），来找到最小化目标函数的值。贝叶斯方法与随机或网格搜索的不同之处在于，它在尝试下一组超参数时，会参考之前的评估结果，因此可以省去很多无用功。贝叶斯调参发使用不断更新的概率模型，通过推断过去的结果来==“集中”==有希望的超参数。

参考资料：
4. https://blog.csdn.net/tianguiyuyu/article/details/80697223
5. https://blog.csdn.net/Noob_daniel/article/details/76087829
6. https://tianchi.aliyun.com/notebook-ai/detail?spm=5176.12586969.1002.18.1cd8593aw4bbL5&postId=95460
7. https://www.jianshu.com/p/ab89df9759c8