小白的机器学习之路(1)---Kaggle竞赛:泰坦尼克之灾(Titanic Machine Learning from Disaster)
我是目录
- 前言
- 数据导入
- 可视化分析
- Pclass
- Sex
- Age
- SibSp
- Parch
- Fare
- Cabin
- Embarked
- 特征提取
- Title
- Family Size
- Companion
- Age band
- Deck
- Embarked & Fare
- 建模
前言
本文以kaggle竞赛中经典的入门案例–泰坦尼克之灾(Titanic Machine Learning from Disaster )为例,直接上手实战。
推荐一篇路易斯安那州立大学的作业报告,其文中对数据特征的分析归纳还是挺有参考价值的。
数据导入
第一步当然是要先获取到我们需要的数据啦,网址如下:
kaggle网址
进入页面后将下图中的training set和test set两个csv文件保存到本地工程文件夹内。

本文代码的运行环境是Anaconda 的 jupyter notebook。个人感觉其无论是下载、管理各类三方库还是做笔记都十分方便好用,强烈推荐!
首先导入数据分析常用的库。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
还需要以下代码在notebook中显示图像以及在图表中做到正常的中文显示。
#图像显示
%matplotlib inline
#中文显示
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#图像尺寸大小
plt.rcParams['figure.figsize'] = (15,8)
导入数据集
data_train = pd.read_csv('D:/WDforJupyter/titanic/train.csv')
data_test = pd.read_csv('D:/WDforJupyter/titanic/test.csv')
下面看一下我们的训练集数据:

也可以使用head(n)来只显示训练集的前n行数据:

我们可以初步了解到可供挖掘分析的数据属性有:
- PassengerId(乘客id,目测没啥用)
- Survived (是否存活,本案例中需要预测的对象)
- Pclass (船票等级,可能会影响到结果)
- Name (姓名,有深入挖掘的潜力)
- Sex (性别,应该女士优先)
- Age (年龄,老幼存活概率应该较大)
- SibSp (船上兄弟姐妹以及配偶的数目,可能会有用)
- Parch (船上父母以及子女的数目,或许有影响)
- Ticket (票号,可能没用)
- Fare (票价,可能有关)
- Cabin (船舱编号,或许有影响)
- Embarked (登船的港口,应该和结果关系不大)
接着看一下数据的概况:

如上,可以看到一共有891位乘客,部分数据特征有缺损。其中年龄这项有714个条目,而客舱这项更是只有204条记录。这些缺失项肯定会需要一些手段来处理补足,目前暂时不表。

上表可以看到特征数据更详细的一些信息。其中值得关注的是年龄与票价这两项的标准差较大,分别达到了14.5264与49.69。针对这样分布范围比较广、波动较大的数据,可以像吴恩达老师建议的那样做归一化(Normalization)处理。
可视化分析
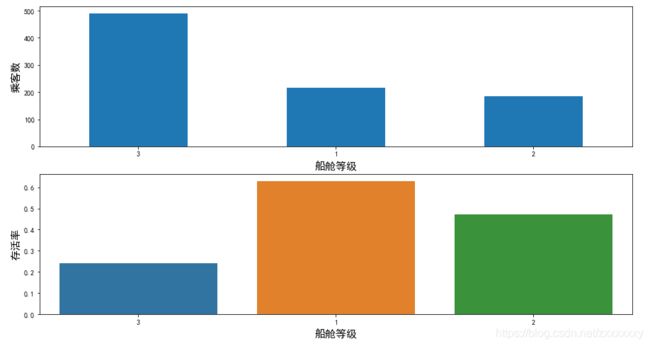
Pclass
首先来看一下乘客的船舱等级会不会影响到获救的概率。
plt.subplot2grid((2,1),(0,0))
data_train.Pclass.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.ylabel('乘客数',{'size':15})
plt.xlabel('船舱等级',{'size':15})
plt.subplot2grid((2,1),(1,0))
sns.barplot(x='Pclass', y='Survived', data=data_train,order=[3,1,2],ci=0)
plt.ylabel('存活率',{'size':15})
plt.xlabel('船舱等级',{'size':15})
Sex
盲猜女性获救比例更高一些。
plt.subplot2grid((2,1),(0,0))
data_train.Sex.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.ylabel('乘客数',{'size':15})
plt.xlabel('性别',{'size':15})
plt.subplot2grid((2,1),(1,0))
sns.barplot(x='Sex', y='Survived', data=data_train,ci=0)
plt.ylabel('存活率',{'size':15})
plt.xlabel('性别',{'size':15})
 可以看到性别因素对生还率有着极为显著的影响。都说在直面生死存亡的关头才能看出一个人的品性。。。这里不得不赞一句:泰坦尼克号上的男同胞们太man了啊!!!
可以看到性别因素对生还率有着极为显著的影响。都说在直面生死存亡的关头才能看出一个人的品性。。。这里不得不赞一句:泰坦尼克号上的男同胞们太man了啊!!!
Age
下面一起来看看对老幼的保护怎么样
data_train.Age[data_train.Survived==1].plot(kind='kde')
data_train.Age[data_train.Survived==0].plot(kind='kde')
plt.legend(['Survived==1','Survived==0'])
plt.xlim((0,80))
plt.ylabel('密度',{'size':15})
plt.xlabel('年龄',{'size':15})

年龄在15岁以下的乘客其生还的密度曲线还是远高于不幸的密度曲线的,但是长者的获救概率似乎就没有这么高了。可能他们自愿将生存的机会留给了下一代;也可能其本身较差的体质加上受到的关注没有孩童来的多导致总体获救概率与青壮一带堪堪齐平;当然一定还有其他没考虑进来的因素导致了这个现象,后续我们可以再深入挖掘。
SibSp
Sibling and Spouses(我为什么要用s?) 属性代表该名乘客有多少兄弟姐妹以及配偶一同登上了这艘不幸的邮轮。理论上来说人多力量大,多几个同行的人互相照应可以在灾难中提升生还几率,下面来看一下到底是不是这样。
plt.subplot2grid((2,1),(0,0))
data_train.SibSp.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.ylabel('乘客数',{'size':15})
plt.xlabel('兄弟姐妹及配偶数目',{'size':15})
plt.subplot2grid((2,1),(1,0))
sns.barplot(x='SibSp', y='Survived', data=data_train,ci=0)
plt.ylabel('存活率',{'size':15})
plt.xlabel('兄弟姐妹及配偶数目',{'size':15})
Parch
Parents and children特征表明该名乘客在船上共有多少直系亲属(父母以及子女)。
plt.subplot2grid((2,1),(0,0))
data_train.Parch.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.ylabel('乘客数',{'size':15})
plt.xlabel('父母子女数目',{'size':15})
plt.subplot2grid((2,1),(1,0))
sns.barplot(x='Parch', y='Survived', data=data_train,ci=0)
plt.ylabel('存活率',{'size':15})
plt.xlabel('父母子女数目',{'size':15})
Fare
票价属性应该和船舱等级的作用类似:富有、社会地位较高的人会在逃生过程中得到更多的资源倾斜。
data_train.Fare[data_train.Survived==1].plot(kind='kde')
data_train.Fare[data_train.Survived==0].plot(kind='kde')
plt.legend(['Survived==1','Survived==0'])
plt.xlim((0,300))
plt.ylabel('密度',{'size':15})
plt.xlabel('票价',{'size':15})

票价在大约30到150之间的乘客的生还率显著高于其他区间的人。
Cabin
可以粗略看到舱号的形式为首字母+数字的形式。根据经验,前面的字母一般代表该舱房所处的甲板编号或者楼层号,后面的数字则为具体的房间号。那么自然可以想到富人和穷人分别居住的一等舱以及三等舱所处的甲板号(或楼层号)一定是不同的。

我们下面把甲板号提取出来看一下有什么影响
plt.subplot2grid((2,1),(0,0))
data_train.Cabin.str.get(0).value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.xlabel('甲板编号',{'size':15})
plt.ylabel('乘客数目',{'size':15})
plt.subplot2grid((2,1),(1,0))
data_train['Deck']=data_train.Cabin.str.get(0)
sns.barplot(x='Deck',y='Survived',data=data_train,ci=0,order=['C','B','D','E','A','F','G','T'])
plt.xlabel('甲板编号',{'size':15})
plt.ylabel('存活率',{'size':15})
Embarked
C = Cherbourg, Q = Queenstown, S = Southampton
plt.subplot2grid((2,1),(0,0))
data_train.Embarked.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.ylabel('乘客数',{'size':15})
plt.xlabel('登船港口',{'size':15})
plt.subplot2grid((2,1),(1,0))
sns.barplot(x='Embarked', y='Survived', data=data_train,ci=0)
plt.ylabel('存活率',{'size':15})
plt.xlabel('登船港口',{'size':15})
 看来选择在法国瑟堡登船的人会更好运呢(应该是那边登船的乘客组成以名流居多吧)
看来选择在法国瑟堡登船的人会更好运呢(应该是那边登船的乘客组成以名流居多吧)
特征提取
首先放一个血的教训。。
![]() 一定要把训练集和测试集先合到一起做特征工程啊!!!
一定要把训练集和测试集先合到一起做特征工程啊!!!
Title
把姓名中的称呼头衔提取出来
data_train = pd.read_csv('D:/WDforJupyter/titanic/train.csv')
data_test = pd.read_csv('D:/WDforJupyter/titanic/test.csv')
data_set = pd.concat([data_train, data_test], ignore_index = True)
data_set['Title']=data_set['Name'].apply(lambda i:i.split(',')[1].split('.')[0])
data_set.Title.value_counts()

谷歌了一下他们的含义,网上的很多信息比较模糊甚至矛盾,有不对的地方欢迎指正~
| Title | 称呼/头衔 |
|---|---|
| Mr | 先生 |
| Miss | 女士/小姐 |
| Mrs | 太太/夫人 |
| Master | 大师 |
| Dr (Dotcor) | 博士/医生 |
| Rev (Reverend) | 牧师/教士 |
| Major | 少校 |
| Col (Colonel) | 上校 |
| Mlle(Mademoiselle) | 小姐(法语) |
| Don | 一种(男性)敬称(西班牙语) |
| Dona | 一种(女性)敬称(西班牙语) |
| Sir | 阁下/爵士 |
| Jonkheer | 一种用于贵族男性后裔的敬称 |
| Mme (Madame) | 夫人(法语) |
| Lady | 领主夫人/有地位的女士小姐 |
| the Countess | 相当于(女)伯爵 |
| Ms | 女士 |
| Capt (Captain) | 上尉/船长 |
再对这些title进行大致的分类
f=lambda row:row.split(',')[1].split('.')[0].strip()
data_set['Title'] = data_set['Name'].apply(f)
Title = {}
Title.update(dict.fromkeys(['Capt', 'Col', 'Major'], '军官'))
Title.update(dict.fromkeys(['Don', 'Sir','Jonkheer'], '贵族男性'))
Title.update(dict.fromkeys(['the Countess', 'Lady','Dona'], '贵族女性'))
Title.update(dict.fromkeys(['Mme', 'Ms', 'Mrs','Mlle', 'Miss'], '普通女性'))
Title.update(dict.fromkeys(['Mr'], '普通男性'))
Title.update(dict.fromkeys(['Master','Dr','Rev'], '受尊崇的人'))
data_set['Title'] = data_set['Title'].map(Title)
plt.subplot2grid((2,1),(0,0))
sns.barplot(x='Title', y='Survived', data=data_set,ci=0,order=['普通男性','普通女性','受尊崇的人','军官','贵族男性','贵族女性'])
plt.xlabel('头衔',{'size':15})
plt.ylabel('存活率',{'size':15})
plt.subplot2grid((2,1),(1,0))
data_set.Title.value_counts().plot(kind='bar')
plt.xticks(rotation=0)
plt.xlabel('头衔',{'size':15})
plt.ylabel('人数',{'size':15})

贵族身份加女性身份在船上简直就是免死金牌!另外,兵哥哥们的表现也值得尊敬。
Family Size
把所有亲属加上自己合成一个新的家庭成员数属性
Family_Size = Parents_Children + Siblings_Spouses + 1
data_set['FamilySize']=data_set['SibSp']+data_set['Parch']+1
sns.barplot(x='FamilySize', y='Survived', data=data_set,ci=0)
plt.xlabel('船上家庭成员数',{'size':15})
plt.ylabel('存活率',{'size':15})
def family_type(x):
if (x >= 2) & (x <= 4):
return '中型家庭'
elif (x > 4):
return '大家庭'
elif (x ==1):
return '单身汪'
data_set['FamilyType']=data_set['FamilySize'].apply(family_type)
sns.barplot(x='FamilyType', y='Survived', data=data_set,ci=0)
plt.xlabel('家庭类型',{'size':15})
plt.ylabel('存活率',{'size':15})
Companion
根据相同的ticket number可以找出那些结伴同行的人。
g=lambda row : data_set.Ticket.value_counts()[row]
data_set['Ticket_feature']=data_set.Ticket.apply(g)
def companion(x):
if (x<2):
return '单身汪'
elif ((x >= 2) & (x <= 4)):
return '2-4人同行'
elif (x > 4):
return '5人及以上同行'
data_set['Companion'] = data_set.Ticket_feature.apply(companion)
sns.barplot(x='Companion', y='Survived', data=data_set,ci=0)
plt.xlabel('同行人数',{'size':15})
plt.ylabel('存活率',{'size':15})
Age band
利用随机森林拟合年龄的缺失值。
from sklearn.ensemble import RandomForestRegressor
age_df = data_set[['Age', 'Pclass','Sex','Title','Parch','SibSp']]
age_df=pd.get_dummies(age_df)
known_age = age_df[age_df.Age.notnull()].values
unknown_age = age_df[age_df.Age.isnull()].values
y = known_age[:, 0]
x = known_age[:, 1:]
rfr = RandomForestRegressor(random_state=0, n_estimators=200, n_jobs=-1)
rfr.fit(x, y)
predictedAges = rfr.predict(unknown_age[:, 1::])
data_set.loc[ (data_set.Age.isnull()), 'Age' ] = predictedAges
进行年龄分组
def age_band(x):
if (x<=15):
return '青少年'
elif ((x >15) & (x <60)):
return '成人'
elif (x >= 60):
return '老人'
data_set['AgeBand'] = data_set.Age.apply(age_band)
sns.barplot(x='AgeBand', y='Survived', data=data_set,ci=0)
plt.xlabel('年龄带',{'size':15})
plt.ylabel('存活率',{'size':15})
Deck
从舱位号的首字母取出甲板号。没有记录的用No来填充。
data_set.loc[ (data_set.Cabin.isnull()), 'Cabin' ] = 'No'
data_set['Deck']=data_set.Cabin.str.get(0)
plt.subplot2grid((2,1),(0,0))
data_set.Cabin.str.get(0).value_counts().plot(kind="bar")
plt.xticks(rotation=0)
plt.xlabel("甲板编号(N为未记录)",{'size':15})
plt.ylabel("乘客数目",{'size':15})
plt.subplot2grid((2,1),(1,0))
data_set['Deck']=data_set.Cabin.str.get(0)
sns.barplot(x='Deck',y='Survived',data=data_set,ci=0,order=['N','C','B','D','E','A','F','G','T'])
plt.xlabel("甲板编号(N为未记录)",{'size':15})
plt.ylabel("存活率",{'size':15})
Embarked & Fare
利用现有的相近属性的中位值来填充缺失值
data_set[data_set.Embarked.isnull()]
data_set.loc[ (data_set.Embarked.isnull()) ] = 'S'
data_set.loc[ (data_set.Fare.isnull()),'Fare' ] = (6.2375+7.25)/2
data_train[data_train['Pclass']==3][data_train['Embarked']=='S'][data_train['Sex']=='male'].groupby(['Age']).Fare.median()
data_test.loc[ (data_test.Fare.isnull()) ,'Fare'] = 6.2375+7.25/2
建模
最后一步就是利用随机森林来对测试集中的数据进行预测啦!
data_set1=data_set[['AgeBand','Pclass','Sex','Fare','Embarked','Title','Companion','Deck','FamilyType']]
data_set2=pd.get_dummies(data_set1)
train=data_set2[:891]
test=data_set2[891:]
train_data_X=train.values
train_data_Y=data_train['Survived'].values
test_data_X=test.values
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
rfc = RandomForestClassifier(random_state = 0,n_estimators = 69,max_features = 'sqrt', criterion='entropy')
rfc.fit(train_data_X,train_data_Y)
scores = cross_val_score(rfc, train_data_X, train_data_Y,cv=5)
print(np.mean(scores))
predictions = rfc.predict(test_data_X)
submission = pd.DataFrame({'PassengerId': data_test.loc[:,'PassengerId'], 'Survived': predictions.astype(np.int32)})
submission.to_csv('submission.csv', index=False)

最后提交上去kaggle给的分数是0.78468,比自己做的交叉验证结果低不少。大家可以在此基础上做一些更精细化的挖掘。
我之后反复尝试,得到最好的成绩如下:
 总算是混进前10%了!!!
总算是混进前10%了!!!