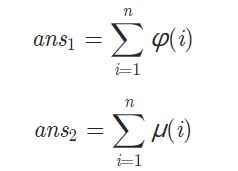1005 huntian oy (HDU 6706)
题意:
其中 T = 10^4,1 <= n,a,b <= 1e9,保证每次 a,b互质。
思路:
首先我们需要知道
公式: gcd(a^n - b^n, a^m - b^m) = a^(gcd(m,n)) - b^(gcd(m,n))
由a,b互质,原式即为
f(n, a, b) = ∑∑ (i-j)*[(i,j)=1] = ∑ (i*∑ [(i, j)=1] ) - ∑∑ j*[(i, j)=1]
然后我们还要知道
欧拉函数定义式: phi(n) = ∑ [(i, n)=1]
1…n中与n互质的数的和: ∑ i*[(i, n)=1] = phi(n)*n / 2,n>1,(n==1时 和为1)
所以
f(n, a, b) = ∑ i*phi(i) - (∑ phi(i)*i/2 + 1/2) = (∑ i*phi(i) - 1) / 2
现在问题变成 求 i*phi(i) 的前缀和。由于 n 很大,达到 10^9,线性时间是不够的,要用到杜教筛。
不懂杜教筛?出门右拐先去这篇博客研究研究。学会了可以先尝试本篇博客后面的模板题:洛谷P4213。
预处理 √n 以内的前缀和后,剩下部分利用整除分块求解的时间复杂度为 O(n^(3/4)),预处理前 k = n^(2/3) 时 时间复杂度可以优化到 O(n^(2/3))。详见大佬的博客分析。
AC代码:
#include#include using namespace std; const int mod = 1e9+7; const int MAXN = 1000000; unordered_map<int, long long> Sumiphi; int prime[MAXN+5], cnt; long long phi[MAXN+5]; long long iphi[MAXN+5]; bool isprime[MAXN+5]; // 线性筛 void getPrime(int n) { isprime[1] = true; phi[1] = 1; for(int i=2;i<=n;i++) { if(!isprime[i]) prime[++cnt] = i, phi[i] = i-1; for(int j=1;j<=cnt&&prime[j]*i<=n;j++) { isprime[prime[j]*i] = true; phi[prime[j]*i] = phi[i]*(prime[j]-1); if(i%prime[j]==0) { phi[prime[j]*i] = phi[i]*(prime[j]); break; } } } // 前缀和 for(int i=1;i<=n;i++) { iphi[i] = iphi[i-1] + phi[i]*i % mod; iphi[i] %= mod; } } const int _two = (1+mod)/2; const int _six = 166666668; // 杜教筛求 ∑i*phi(i) // S(n) = ∑i^2 - ∑d*S(n/d) = n*(n+1)*(2n+1)/6 - ∑d×S(n/d) long long iphiSum(int n) { if(n<=MAXN) return iphi[n]; if(Sumiphi.count(n)) return Sumiphi[n]; long long sum = 0; for(int i=2,j;i<=n;i=j+1) { j = n/(n/i); sum += iphiSum(n/i)*(j-i+1)% mod *(i+j) % mod *_two % mod; } Sumiphi[n] = ((1LL*n*(n+1)% mod *(2*n+1)% mod *_six % mod - sum)%mod + mod) % mod; return Sumiphi[n]; } // 答案: // ( Sum(i*phi(i)) - 1 ) /2 int main() { getPrime(MAXN); int T, n, a, b; scanf("%d", &T); while(T--) { scanf("%d %d %d", &n, &a, &b); printf("%lld\n", (iphiSum(n)-1+mod)%mod * _two % mod); } return 0; }
P4213 【模板】杜教筛(Sum)
题意:
给定一个正整数 N (N<=2^31-1),求
AC模板:
#include#include using namespace std; // 参考自:https://www.cnblogs.com/dreagonm/p/10077979.html const int MAXN = 5000000; unordered_map<int, long long> Sumphi; unordered_map<int, long long> Summu; int prime[MAXN+5], cnt; long long mu[MAXN+5], phi[MAXN+5]; bool isprime[MAXN+5]; // 线性筛 void getPrime(int n) { isprime[1] = true; mu[1] = 1; phi[1] = 1; for(int i=2;i<=n;i++) { if(!isprime[i]) prime[++cnt] = i, phi[i] = i-1, mu[i] = -1; for(int j=1;j<=cnt&&prime[j]*i<=n;j++) { isprime[prime[j]*i] = true; mu[prime[j]*i] = -mu[i]; phi[prime[j]*i] = phi[i]*(prime[j]-1); if(i%prime[j]==0) { mu[prime[j]*i] = 0; phi[prime[j]*i] = phi[i]*(prime[j]); break; } } } // 前缀和 for(int i=1;i<=n;i++) { mu[i] += mu[i-1]; phi[i] += phi[i-1]; } } // 杜教筛求 ∑u(i) // S(n) = 1 - ∑S(n/d) long long muSum(int n) { if(n<=MAXN) return mu[n]; if(Summu.count(n)) return Summu[n]; int sum = 0; for(int i=2,j;i<=n;i=j+1) { j = n/(n/i); sum += (j-i+1)*muSum(n/i); } Summu[n] = 1 - sum; return Summu[n]; } // 杜教筛求 ∑phi(i) // S(n) = ∑ i - ∑S(n/d) long long phiSum(int n) { if(n<=MAXN) return phi[n]; if(Sumphi.count(n)) return Sumphi[n]; long long sum = 0; for(int i=2,j;i<=n;i=j+1) { j = n/(n/i); sum += (j-i+1)*phiSum(n/i); } Sumphi[n] = 1LL*(n+1)*n/2 - sum; return Sumphi[n]; } int main() { getPrime(MAXN); int T, n; scanf("%d", &T); while(T--) { scanf("%d", &n); printf("%lld %d\n", phiSum(n), muSum(n)); } return 0; }