3D数学-透视投影
文章目录
- 3D数学-透视投影
- 概述
- 近大远小
- 视锥体
- 投影矩阵的本质
- 投影矩阵推导
- 投影矩阵的另一种形式
- z-fighting
3D数学-透视投影
好记性不如烂笔头啊,还是记录一下!
概述
投影变换完成的是如何将三维模型显示到二维视口上,这是一个三维到二维的过程。你可以将投影变换看作是调整照相机的焦距,它模拟了为照相机选择镜头的过程。投影变换是所有变换中最复杂的一个。
近大远小
近大远小是众所周知的光学现象。之所以出现这种现象,是因为离人眼近的物体在视网膜上的投影大,而离眼睛远的物体在视网膜上的投影小。如下图所示,红色箭头和蓝色箭头的高度相同,但是蓝色箭头离眼睛近,因此它在视网膜上的投影,要大于红色箭头的投影。
然而物体看上去的大小,除了与它离眼睛的远近有关,还和物体本身的尺寸有关。视角(angle of view 或者 field of view 视域)可以取代上述两者,直接比较物体看上去的大小。在计算机图形学中,为了让三维物体显示在屏幕上有立体感,有必要模拟人眼近大远小这一个特性,利用透视投影矩阵可以方便地完成这项任务。
视锥体
视锥体是一个三维体,他的位置和摄像机相关,视锥体的形状决定了模型如何从camera space投影到屏幕上。透视投影使用棱锥作为视锥体,摄像机位于棱锥的椎顶。该棱锥被前后两个平面截断,形成一个棱台,叫做View Frustum,只有位于Frustum内部的模型才是可见的。我们也通常称这个为裁剪空间,在这个裁剪空间中有两个平面比较特殊,我们分辨称为近裁剪平面(near clip plane)和远裁剪平面(far clip plane)。
投影矩阵的本质
投影矩阵有两个目的:
- 首先是为投影做准备。这是个迷惑点。虽然投影矩阵的名称包含了投影二字,但是它并没有进行真正的投影工作,而是在为投影做准备。真正得投影发生在后面得
齐次除法(homogeneous division)过程中。经过投影矩阵的变换后,顶点的w分量会具有特殊的意义。 - 其次是对 x x x, y y y, z z z分量进行缩放。如果用视锥体的6个裁剪平面来进行裁剪会比较麻烦,而经过投影矩阵的缩放后,久可以直接使用 w w w分量作为一个范围值。如果 x x x, y y y, z z z分量都位于这个范围内,就说明该顶点位于裁剪空间内,如下图所示:
投影矩阵推导
如图所示:
< x e , y e , z e >
< x p , y p , z p > 近裁剪平面(near clip plane)上的投影坐标
< x n , y n , z n > 规范化设备坐标系(Normalized Device Coordinates)中的坐标
l l l表示近裁剪平面(near clip plane)的左边,即 x = l x=l x=l
r r r表示近裁剪平面(near clip plane)的右边,即 x = r x=r x=r
t t t表示近裁剪平面(near clip plane)的上边,即 y = t y=t y=t
b b b表示近裁剪平面(near clip plane)的下边,即 y = b y=b y=b
有以下关系式:
x e x p = z e − n \frac{x_{e}}{x_{p}}=\frac{z_{e}}{-n} xpxe=−nze
可解出得:
x p = − n x e z e x_{p}=-\frac{nx_{e}}{z_{e}} xp=−zenxe
同理:
y p = − n y e z e y_{p}=-\frac{ny_{e}}{z_{e}} yp=−zenye
现在需要将 x p x_{p} xp映射到 x n x_{n} xn, x p x_{p} xp得范围是 [ l , r ] [l, r] [l,r], x n x_{n} xn得范围是 [ − 1 , 1 ] [-1, 1] [−1,1],可以利用简单线性插值的方法获得以下关系式:
x p − l r − l = x n − ( − 1 ) 1 − ( − 1 ) \frac{x_{p}-l}{r-l}=\frac{x_{n}-(-1)}{1-(-1)} r−lxp−l=1−(−1)xn−(−1)
同理可得到以下方程组:
{ x p − l r − l = x n − ( − 1 ) 1 − ( − 1 ) y p − b t − b = y n − ( − 1 ) 1 − ( − 1 ) x p = − n x e z e y p = − n y e z e \begin{cases} \frac{x_{p}-l}{r-l}=\frac{x_{n}-(-1)}{1-(-1)} \\[2ex] \frac{y_{p}-b}{t-b}=\frac{y_{n}-(-1)}{1-(-1)} \\[2ex] x_{p}=-\frac{nx_{e}}{z_{e}} \\[2ex] y_{p}=-\frac{ny_{e}}{z_{e}} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧r−lxp−l=1−(−1)xn−(−1)t−byp−b=1−(−1)yn−(−1)xp=−zenxeyp=−zenye
可解出得:
{ x n = ( − x e z e ) 2 n r − l − r + l r − l y n = ( − y e z e ) 2 n t − b − t + b t − b \begin{cases} x_{n}=(-\frac{x_{e}}{z_{e}})\frac{2n}{r-l}-\frac{r+l}{r-l} \\[2ex] y_{n}=(-\frac{y_{e}}{z_{e}})\frac{2n}{t-b}-\frac{t+b}{t-b} \end{cases} ⎩⎨⎧xn=(−zexe)r−l2n−r−lr+lyn=(−zeye)t−b2n−t−bt+b
最后看看 z n z_{n} zn,当视锥体内的顶点投影到近裁剪平面(near clip plane)的时候,实际上 z p z_{p} zp的值已经没有意义了,因为所有近裁剪平面(near clip plane)上的点,他们的 z p z_{p} zp值都是-n,看起来我们甚至可以抛弃这个 z p z_{p} zp值,可以么?当然不行!不要忘记还有深度测试。 < x e , y e , z e >
z n = A z e + B z_{n}=\frac{A}{z_{e}}+B zn=zeA+B
在映射前, z e z_{e} ze的范围是 [ − f , − n ] [-f,-n] [−f,−n]。在映射后, z e z_{e} ze的范围是 [ − 1 , 1 ] [-1,1] [−1,1]。需要找到 − n → − 1 -n \rightarrow -1 −n→−1, − f → 1 -f \rightarrow 1 −f→1的映射关系(该映射应该将z坐标反向,因为齐次裁剪空间为左手坐标系), 将数据代入上面的一次式,可得下面的方程组:
{ − 1 = A − n + B 1 = A − f + B \begin{cases} -1=\frac{A}{-n}+B \\[2ex] 1=\frac{A}{-f}+B \end{cases} ⎩⎨⎧−1=−nA+B1=−fA+B
解出可得:
{ A = 2 n f f − n B = f + n f − n \begin{cases} A=\frac{2nf}{f-n} \\[2ex] B=\frac{f+n}{f-n} \end{cases} ⎩⎨⎧A=f−n2nfB=f−nf+n
可以得到 z z z坐标映射到 [ − 1 , 1 ] [-1,1] [−1,1]的映射函数为:
z n = − 2 n f f − n ( − 1 z e ) + f + n f − n z_{n}=-\frac{2nf}{f-n}(-\frac{1}{z_{e}})+\frac{f+n}{f-n} zn=−f−n2nf(−ze1)+f−nf+n
整理可得:
{ x n = ( − x e z e ) 2 n r − l − r + l r − l y n = ( − y e z e ) 2 n t − b − t + b t − b z n = ( − 1 z e ) ( − 2 n f f − n ) + f + n f − n \begin{cases} x_{n}=(-\frac{x_{e}}{z_{e}})\frac{2n}{r-l}-\frac{r+l}{r-l} \\[2ex] y_{n}=(-\frac{y_{e}}{z_{e}})\frac{2n}{t-b}-\frac{t+b}{t-b} \\[2ex] z_{n}=(-\frac{1}{z_{e}})(-\frac{2nf}{f-n})+\frac{f+n}{f-n} \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧xn=(−zexe)r−l2n−r−lr+lyn=(−zeye)t−b2n−t−bt+bzn=(−ze1)(−f−n2nf)+f−nf+n
可以发现以上等式中都除以 − z e -z_{e} −ze,则3D点 < x n , y n , z n >
< − x n z e , − y n z e , − z n z e , − z e > <-x_{n}z_{e}, -y_{n}z_{e}, -z_{n}z_{e}, -z_{e}> <−xnze,−ynze,−znze,−ze>
则 − x n z e -x_{n}z_{e} −xnze, − y n z e -y_{n}z_{e} −ynze, − z n z e -z_{n}z_{e} −znze分别为:
{ − x n z e = x e 2 n r − l + z e r + l r − l − y n z e = y e 2 n t − b + z e t + b t − b − z n z e = z e ( − f + n f − n ) − 2 n f f − n \begin{cases} -x_{n}z_{e}=x_{e}\frac{2n}{r-l}+z_{e}\frac{r+l}{r-l} \\[2ex] -y_{n}z_{e}=y_{e}\frac{2n}{t-b}+z_{e}\frac{t+b}{t-b} \\[2ex] -z_{n}z_{e}=z_{e}(-\frac{f+n}{f-n})-\frac{2nf}{f-n} \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧−xnze=xer−l2n+zer−lr+l−ynze=yet−b2n+zet−bt+b−znze=ze(−f−nf+n)−f−n2nf
以上函数组为点 P e P_{e} Pe的线性函数组,因此可以用一个 4 × 4 4 \times 4 4×4的矩阵 M f r u s t u m M_{frustum} Mfrustum来表示 P n P_{n} Pn点的计算公式:
P n = M f r u s t u m ⋅ P e = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 − f + n f − n − 2 n f f − n 0 0 − 1 0 ] ⋅ [ x e y e z e 1 ] P_{n} = M_{frustum} \cdot P_{e} = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\[2ex] 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\[2ex] 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\[2ex] 0 & 0 & -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_{e} \\[2ex] y_{e} \\[2ex] z_{e} \\[2ex] 1 \end{bmatrix} Pn=Mfrustum⋅Pe=⎣⎢⎢⎢⎢⎢⎢⎡r−l2n0000t−b2n00r−lr+lt−bt+b−f−nf+n−100−f−n2nf0⎦⎥⎥⎥⎥⎥⎥⎤⋅⎣⎢⎢⎢⎢⎢⎢⎡xeyeze1⎦⎥⎥⎥⎥⎥⎥⎤
M f r u s t u m M_{frustum} Mfrustum就是最终的透视变换矩阵。相机空间中的顶点,如果在视锥体中,则变换后就在规范化设备坐标系(Normalized Device Coordinates)中。如果在视锥体外,变换后就在规范化设备坐标系(Normalized Device Coordinates)外,而规范化设备坐标系(Normalized Device Coordinates)本身的规则性对于多边形的裁剪很有利。
投影矩阵的另一种形式
视角(angle of view 或者 field of view 视域)是视锥体再 x z xz xz平面或者 y z yz yz平面的开角角度,也可以用来描述透视投影矩阵。具体哪个平面都可以,OpenGL和D3D都使用 y z yz yz平面,Aspect是投影平面的宽高比,如图所示:
可以得到一下关系式:
{ A s p e c t = r t t = n × tan f o v 2 b = − t r = t × A s p e c t l = − r \begin{cases} Aspect = \frac{r}{t} \\[2ex] t = n \times \tan\frac{fov}{2} \\[2ex] b = -t \\[2ex] r = t \times Aspect \\[2ex] l = -r \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧Aspect=trt=n×tan2fovb=−tr=t×Aspectl=−r
所以 M f r u s t u m M_{frustum} Mfrustum还可以写成:
M f r u s t u m = [ cot f o v 2 A s p e c t 0 0 0 0 cot f o v 2 0 0 0 0 − f + n f − n − 2 n f f − n 0 0 − 1 0 ] M_{frustum}= \begin{bmatrix} \frac{\cot\frac{fov}{2}}{Aspect} & 0 & 0 & 0 \\[2ex] 0 & \cot\frac{fov}{2} & 0 & 0 \\[2ex] 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\[2ex] 0 & 0 & -1 & 0 \end{bmatrix} Mfrustum=⎣⎢⎢⎢⎢⎢⎢⎢⎡Aspectcot2fov0000cot2fov0000−f−nf+n−100−f−n2nf0⎦⎥⎥⎥⎥⎥⎥⎥⎤
z-fighting
还有一点需要额外注意,上述变换矩阵的过程中, x n x_{n} xn和 x e x_{e} xe, y n y_{n} yn和 y e y_{e} ye是线性的,但是 z n z_{n} zn和 z e z_{e} ze是非线性的:
z n = ( − 1 z e ) ( − 2 n f f − n ) + f + n f − n z_{n}=(-\frac{1}{z_{e}})(-\frac{2nf}{f-n})+\frac{f+n}{f-n} zn=(−ze1)(−f−n2nf)+f−nf+n
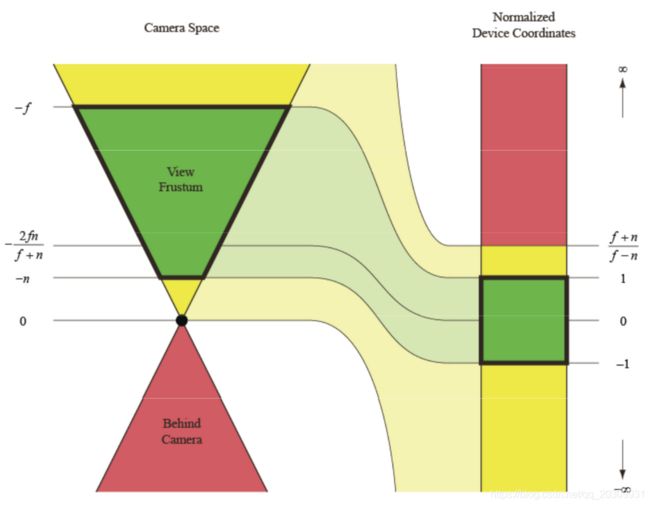
z e z_{e} ze越接近 − f -f −f, z n z_{n} zn越接近1, z e z_{e} ze越接近 − n -n −n, z n z_{n} zn越接近-1。也就是说, z n z_{n} zn越大,离相机越远,反之离相机越近。 z n z_{n} zn随 z e z_{e} ze的变化关系如下图所示:
通过观察左侧图,我们发现:当相机坐标系中的点越接近近裁剪平面(near clip plane)时, z e z_{e} ze上发生的微小变化都会导致 z n z_{n} zn的剧烈变化;而当点越接近远裁剪平面(far clip plane)时, z n z_{n} zn对 z e z_{e} ze上发生的变化不敏感。在做渲染时, z z z方向的绝对深度并没有意义,我们只需要知道各点的相对深度,确定遮挡关系,保证靠近相机的点挡住它后面离相机远的点即可。因此,越接近近裁剪平面(near clip plane)的点,它的深度渲染就越准确,而越接近远裁剪平面(far clip plane)的点,它的深度渲染就越不准确。
此外,对比上面的左右两幅图,我们发现:当远裁剪平面(far clip plane)和近裁剪平面(near clip plane)距离较大时,接近远裁剪平面(far clip plane)的点的 z n z_{n} zn对 z e z_{e} ze的变化十分不敏感,这样导致的问题称为z-fighting。因此,在条件允许的情况下,应该尽量减小两个裁剪平面之间的距离。
附一张 z z z方向的映射关系图:
饮水思源
参考文献:
《3D游戏与图形学中的数学方法》
《透视投影详解》
《Perspective Projection Matrix 透视投影矩阵的推导》
《图形学扫盲–(2)透视投影(Perspective Projection)》
版权声明:原创技术文章,撰写不易,转载请注明出处!