HDU 5531（2015长春 icpc E.Rebuild） 计算几何

Rebuild

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1881 Accepted Submission(s): 416

Problem Description
Archaeologists find ruins of Ancient ACM Civilization, and they want to rebuild it.
The ruins form a closed path on an x-y plane, which has n endpoints. The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively. Endpoint i and endpoint i−1 are adjacent for 1 < i ≤ n, also endpoint 1 and endpoint n are adjacent. Distances between any two adjacent endpoints are positive integers.

To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri. All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.

Note that ri must not be less than 0 since we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.

You are given the coordinates of n endpoints. Your task is to find r1,r2,…,rn which makes sum of base area of all pillars as minimum as possible.
For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12), we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25). The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816…. Note that we count the area of the overlapping parts multiple times.

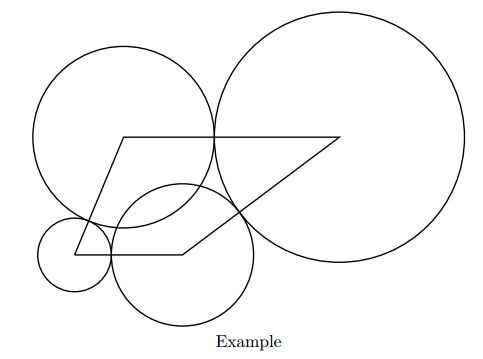
If there are several possible to produce the minimum sum of base area, you may output any of them.

Input
The first line contains an integer t indicating the total number of test cases. The following lines describe a test case.

The first line of each case contains one positive integer n, the size of the closed path. Next n lines, each line consists of two integers (xi,yi) indicate the coordinate of the i-th endpoint.

1≤t≤100
3≤n≤104
|xi|,|yi|≤104
Distances between any two adjacent endpoints are positive integers.

Output
If such answer doesn’t exist, then print on a single line “IMPOSSIBLE” (without the quotes). Otherwise, in the first line print the minimum sum of base area, and then print n lines, the i-th of them should contain a number ri, rounded to 2 digits after the decimal point.

If there are several possible ways to produce the minimum sum of base area, you may output any of them.

Sample Input
3
4
0 0
11 0
27 12
5 12
5
0 0
7 0
7 3
3 6
0 6
5
0 0
1 0
6 12
3 16
0 12

Sample Output
988.82
3.75
7.25
12.75
9.25
157.08
6.00
1.00
2.00
3.00
0.00
IMPOSSIBLE

题意：这道题目按顺序给出一些点的坐标，点依次相连，并且最后一个点和第一个点相连形成一个环。问在换上以每个点为圆心作一系列圆，要求相邻两点的圆相互外切。如不存在这样的点则输出“IMPOSSIBLE”否则输出这些圆总面积的最小值，并依次输出此时所有圆的半径（所有输出保留两位小数）

分析：我们可以假设第一个圆的半径为x那么能够一次表示出所有的圆的半径，并且可以把每个圆的半径依次表示为f[i] + x,或者f[i] - x;（第i个点）i为奇数是是+，偶数是-；因为要求所有的半径大于等于0，那么我们在可以一次求出所有的f[i]先，和x的范围[minn, maxn]。最后可以用x表示出最后一个圆的半径。
如果是奇数个点：那么x是一个可以求的定值，只要判断在不在[minn, maxn]里就可以，如果在则有解，那么可以通过f[i]求出所有圆的半径，面积也容易求。
如果是偶数个点：那么最后的半径和第一个圆的半径是同号码的，那么不能直接求出x，我们可以用x来表示每一个圆的半径，那么总面积一定能表示称一个x的二次函数，然后结合x在区间[minn, maxn]内，可以求出最大的总面积，并求出此时的x。然后可以求出每个圆的半径。

代码

//
//  main.cpp
//  HDU-Fighting
//
//  Created by  绿色健康文艺小清新 on ...
//  Copyright 2016年  绿色健康文艺小清新. All rights reserved.
//

#include 
#include 

const double PI = acos(-1);//之前吧pi写成3.1415926白wa了一发，pi以后都写成acos(-1)不要无故的wa
const double eps = 1e-7;

int n;
double len[10005], f[10005], x;

struct point{
    double x, y;
} p[10005];

double cal_len(point a, point b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

void cal_all_len()//一次求出所有边的长
{
    for(int i = 0; i < n - 1; i++)
        len[i] = cal_len(p[i], p[i + 1]);
    len[n - 1] = cal_len(p[0], p[n - 1]);
}

double abs(double x)
{
    if(x > 0)
        return x;
    return -x;
}

void print(double ans)
{
    printf("%.2f\n", ans * PI);
    for(int i = 0; i < n; i++)
    {
        if(i & 1)//我从下标0开始存，所以代码里的i和分析里的第几个奇偶性是相反的
            printf("%.2f\n", f[i] - x);
        else
            printf("%.2f\n", f[i] + x);
    }
}

int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        double maxn = 0x3f3f3f, minn = 0;

        scanf("%d", &n);
        for(int i = 0; i < n; i++)
            scanf("%lf%lf", &p[i].x, &p[i].y);

        cal_all_len();

        f[0] = 0;
        for(int i = 1; i < n; i++)
        {
            f[i] = len[i - 1] - f[i - 1];
            if((i & 1) && f[i] < maxn)
                maxn = f[i];
            if(!(i & 1) && (-f[i]) > minn)
                minn = -f[i];
        }
        if(minn >= maxn + eps)
        {
            printf("IMPOSSIBLE\n");
            continue;
        }

        if(n & 1)
        {
            x = 1.0 * (len[n - 1] - f[n -1]) / 2;
            if(x <= minn - eps || x >= maxn + eps)
            {
                printf("IMPOSSIBLE\n");
                continue;
            }

            double ans = 0.0;
            for(int i = 0; i < n; i++)
            {
                if(i & 1)
                    ans += (f[i] - x) * (f[i] - x);
                else
                    ans += (f[i] + x) * (f[i] + x);
            }

            print(ans);
        }
        else
        {
            if(abs(f[n - 1] - len[n - 1]) > eps || (minn - maxn) > eps)
            {
                printf("IMPOSSIBLE\n");
                continue;
            }

            double A = 0, B = 0, C = 0;
            for(int i = 0; i < n; i++)
            {
                A = A + 1;
                C += f[i] * f[i];
                if(i & 1)
                    B -= 2 * f[i];
                else
                    B += 2 * f[i];
            }

            double l = (-B / 2) / A;

            if(l < minn + eps)
                x = minn;
            else if(maxn < l + eps)
                x = maxn;
            else
                x = l;

            print(A * x * x + B * x + C);
        }
    }
    return 0;
}