第十四周作业:Anscombe's quartet
Anscombe’s quartet
Anscombe’s quartet comprises of four datasets, and is rather famous. Why? You’ll find out in this exercise.
Part 1
- Compute the mean and variance of both x and y
- Compute the correlation coefficient between x and y
- Compute the linear regression line: y=β0+β1+ϵ y = β 0 + β 1 + ϵ (hint: use statsmodels and look at the Statsmodels notebook)
Part 2
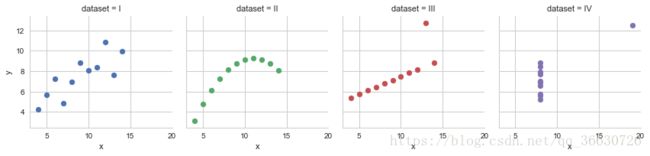
Using Seaborn, visualize all four datasets.
(hint: use sns.FacetGrid combined with plt.scatter)
读取cvs文件
anascombe = pd.read_csv('data.csv')
anascombe.head()
print(anascombe) dataset x y
0 I 10.0 8.04
1 I 8.0 6.95
2 I 13.0 7.58
3 I 9.0 8.81
4 I 11.0 8.33
5 I 14.0 9.96
6 I 6.0 7.24
7 I 4.0 4.26
8 I 12.0 10.84
9 I 7.0 4.82
10 I 5.0 5.68
11 II 10.0 9.14
12 II 8.0 8.14
13 II 13.0 8.74
14 II 9.0 8.77
15 II 11.0 9.26
16 II 14.0 8.10
17 II 6.0 6.13
18 II 4.0 3.10
19 II 12.0 9.13
20 II 7.0 7.26
21 II 5.0 4.74
22 III 10.0 7.46
23 III 8.0 6.77
24 III 13.0 12.74
25 III 9.0 7.11
26 III 11.0 7.81
27 III 14.0 8.84
28 III 6.0 6.08
29 III 4.0 5.39
30 III 12.0 8.15
31 III 7.0 6.42
32 III 5.0 5.73
33 IV 8.0 6.58
34 IV 8.0 5.76
35 IV 8.0 7.71
36 IV 8.0 8.84
37 IV 8.0 8.47
38 IV 8.0 7.04
39 IV 8.0 5.25
40 IV 19.0 12.50
41 IV 8.0 5.56
42 IV 8.0 7.91
43 IV 8.0 6.89计算均值
print(anascombe.groupby('dataset')['x'].mean())
print(anascombe.groupby('dataset')['y'].mean())dataset
I 9.0
II 9.0
III 9.0
IV 9.0
Name: x, dtype: float64
dataset
I 7.500909
II 7.500909
III 7.500000
IV 7.500909
Name: y, dtype: float64计算方差
print(anascombe.groupby('dataset')['x'].var())
print(anascombe.groupby('dataset')['y'].var())dataset
I 11.0
II 11.0
III 11.0
IV 11.0
Name: x, dtype: float64
dataset
I 4.127269
II 4.127629
III 4.122620
IV 4.123249
Name: y, dtype: float64计算相关系数
X1 = anascombe.x[0:10].values
X2 = anascombe.x[11:21].values
X3 = anascombe.x[22:32].values
X4 = anascombe.x[33:43].values
Y1 = anascombe.y[0:10].values
Y2 = anascombe.y[11:21].values
Y3 = anascombe.y[22:32].values
Y4 = anascombe.y[33:43].values
coefficients = [0,0,0,0]
coefficients[0] = sp.stats.pearsonr(X1, Y1)[0] #返回的第一个参数是相关系数
coefficients[1] = sp.stats.pearsonr(X2, Y2)[0]
coefficients[2] = sp.stats.pearsonr(X3, Y3)[0]
coefficients[3] = sp.stats.pearsonr(X4, Y4)[0]
for coefficient in coefficients:
print(coefficient)0.7970815759062526
0.7773093020784241
0.7985632617088811
0.8146722146933596计算线性回归函数
X_I = sm.add_constant(X1) #计算x与y的线性回归
model_I = sm.OLS(Y1, X_I)
result_I = model_I.fit()
params_I = result_I.params
print("DatasetI: y =", params_I[0], "+", params_I[1], "* x")
X_II = sm.add_constant(X2)
model_II = sm.OLS(Y2, X_II)
result_II = model_II.fit()
params_II = result_II.params
print("DatasetII: y =", params_II[0], "+", params_II[1], "* x")
X_III = sm.add_constant(X3)
model_III = sm.OLS(Y3, X_III)
result_III = model_III.fit()
params_III = result_III.params
print("DatasetIII: y =", params_III[0], "+", params_III[1], "* x")
X_IV = sm.add_constant(X4)
model_IV = sm.OLS(Y4, X_IV)
result_IV = model_IV.fit()
params_IV = result_IV.params
print("DatasetIV: y =", params_IV[0], "+", params_IV[1], "* x") DatasetI: y = 2.9018181818181796 + 0.5086363636363637 * x
DatasetII: y = 3.4175974025974023 + 0.4637662337662336 * x
DatasetIII: y = 2.877099567099565 + 0.5106277056277057 * x
DatasetIV: y = 3.023030303030303 + 0.49878787878787884 * x图形化显示(散点图)
sns.set(style='whitegrid')
g = sns.FacetGrid(anascombe, col="dataset", hue="dataset", size=3)
g.map(plt.scatter, 'x', 'y')
plt.show()