leetcode(二) 二分专题
文章目录
- 69.sqrt(x) **
- 35.搜索插入位置
- 34.在排序数组中查找元素的第一个位置和最后一个位置
- 74.搜索二维矩阵 **
- 153.寻找旋转排序数组中的最小值
- 33.搜索旋转排序数组
- 278.第一个错误的版本
- 162.寻找峰值
- 287.寻找重复数
- 275.H指数II
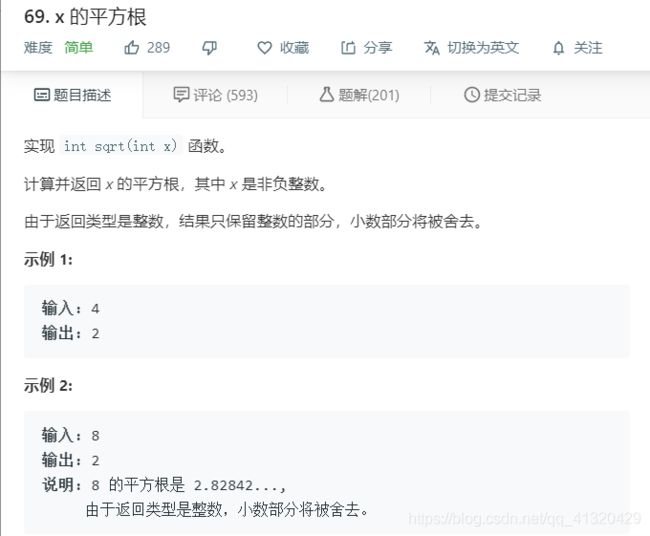
69.sqrt(x) **
被一题简单题边界心态搞崩。。淦
由于这题是取整的,不能用浮点二分那套(二分精确迫近,不用管最后是左还是右界了)
所以这题还是老两样的整数那套迫近
但用老两样问题就来了因为他是整数迫近了就不可能求得精确
比如说我想求8的根(2.8几),最后二分结果要么是2要么是3 都有可能,写的不对就直接TLE,(2,3死循环)
所以一开始想着就找求左界的那个模板,但求左界的模板现在求得是右界。。
因为求不到小数所以 L=mid+1就把他本来的答案变大了,反倒是原来求右界的那个板子求了左界,具体原因还得仔细琢磨,挂个*
- 分割
- 今儿弄懂了,
直截了当的说明
当y老师那两套板子求给定一组数据中没有的数的时候,板子作用就会反过来,–原来求右界的变成求“左”,求左界的变成求“右”
打个比方,比如让我从[1,3,5,6]中求2,那么明显是没有的,这时我想用求左界的板子会输出1还是3呢?答案是3,因为我想从左边逼近答案,结果却没有2,那么最后逼歪了就成了3,所以造成左右反过来的情况
所以这题的情况是一样的
求8的平方根相当于在[0,1,2,3,4,5,6,7,8]数组中找2.8,显然是没有的,所以我一开始用左界的板子会逼近成3,答案肯定就不对了,反而用右界的板子会逼近成2
class Solution {
public:
int mySqrt(int x) {
int l=0,r=x;
while(l<r){
int mid=(l+(long long )r+1)/2; //这里测试数据有x=int的最大取值,可能会爆
if(mid<=x/mid)l=mid;
else r=mid-1;
}
return l;
}
};
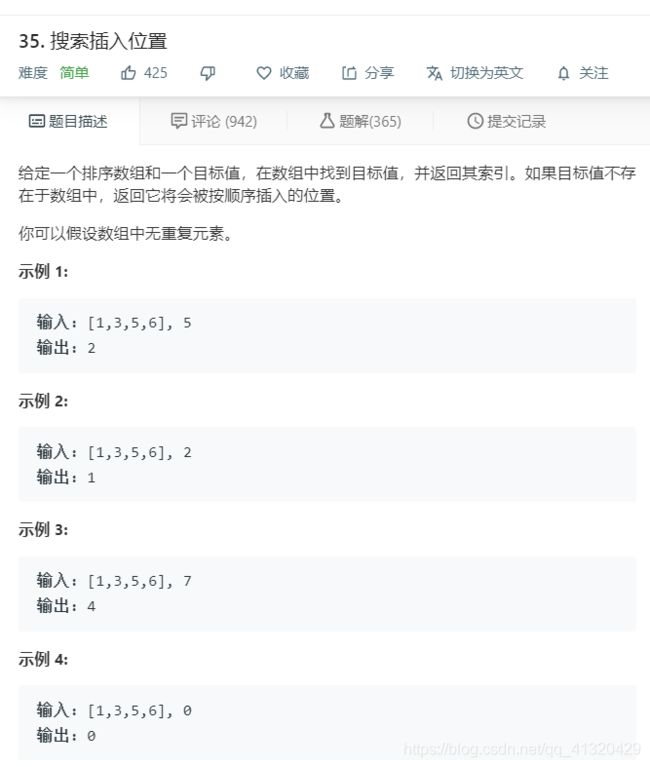
35.搜索插入位置
该题与上题一样,因为待求数可能找不到,所以用求左界的模板靠近"右"值(即应当返回的下标),如果存在该数,直接返回下标即可,注意处理两边界情况
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
if(nums.empty()||nums.back()<target)return nums.size(); //如果数组为空则插入到0位置,target大于最后一个数则插入到最后一个位置
int l=0;
int r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=target)r=mid;
else l=mid+1;
}
return l;
}
};
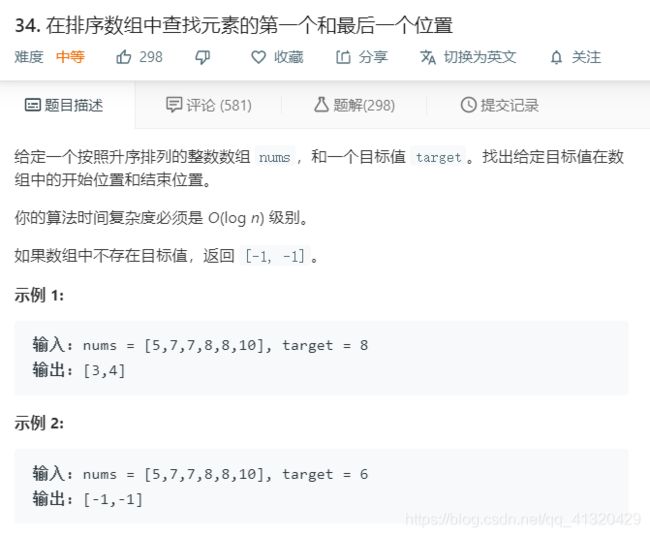
34.在排序数组中查找元素的第一个位置和最后一个位置
模板题,分别求左右边界即可
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.empty())return {-1,-1};
int l=0,r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=target)r=mid;
else l=mid+1;
}
if(nums[l]!=target)return {-1,-1};
int begin =l;
l=0,r=nums.size()-1;
while(l<r){
int mid=l+r+1>>1;
if(nums[mid]<=target)l=mid;
else r=mid-1;
}
int end=l;
return {begin,end};
}
};
74.搜索二维矩阵 **
思路:把二维矩阵想象成一个展开的一维数组进行二分,check时通过公式转化下标
假设矩阵的行n,列m,对应的一维数组元素个数为n*m
一维数组下标为k=0~n * m-1
对应的一维数组和二维数组下标的关系为
m a t r i x [ i ] [ j ] \ matrix[i][j] matrix[i][j]
i = k / m j = k % m \ i=k/m \\ j=k \%m i=k/mj=k%m
注意别写成i=k/n 一开始犯了这个错误hh
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty()||matrix[0].empty())return false; //行列任一为空都返回false
int n=matrix.size(); //行
int m=matrix[0].size(); //列
int l=0,r=n*m-1;
while(l<r){
int mid=l+r>>1;
if(matrix[mid/m][mid%m]>=target)r=mid;
else l=mid+1;
}
if(matrix[r/m][r%m]!=target)return false;
else return true;
}
};
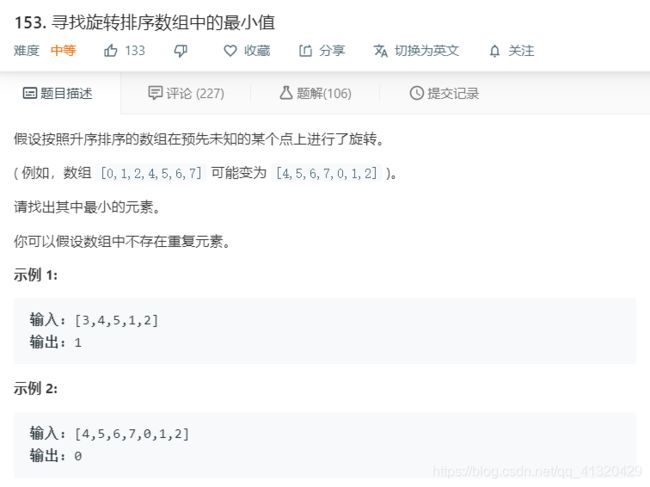
153.寻找旋转排序数组中的最小值
这题就照应y总说的,没有单调性质,一样可以二分
只要能找到一个性质把左右两边分开(比如左边有这个性质,右边没有这个性质)
这题明显就是取数组最后一个数,而左边都大于这个数,右边都小于等于这个数,这样就可以二分了
class Solution {
public:
int findMin(vector<int>& nums) {
if(nums.empty())return NULL;
int l=0,r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]<=nums.back())r=mid; //check的是右半部分
else l=mid+1;
}
return nums[l];
}
};
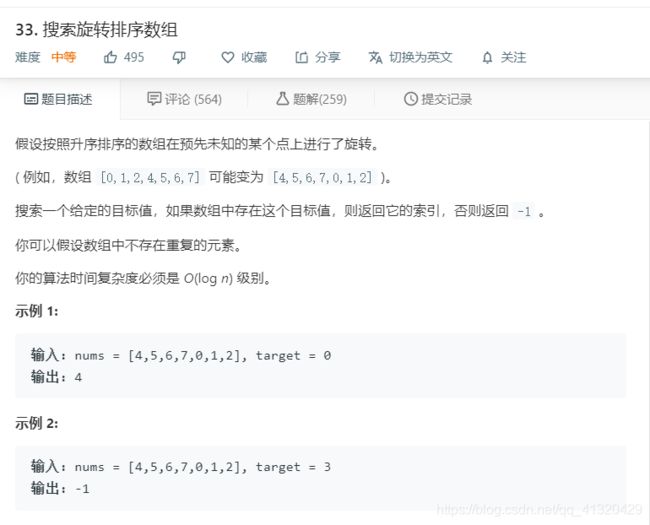
33.搜索旋转排序数组
思路很简单,由上题找到旋转数组的最小值,再通过比较确定target属于左右哪个部分,属于哪个部分对它二分即可
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.empty())return -1;
int l=0,r=nums.size()-1;
while(l<r){
int mid =l+r>>1;
if(nums.back()>=nums[mid])r=mid;
else l=mid+1;
}
if(target<=nums.back())r=nums.size()-1; //判断target属于左右哪一部分
else l=0,r-=1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=target)r=mid;
else l=mid+1;
}
if(nums[l]==target)return l;
else return -1;
}
};
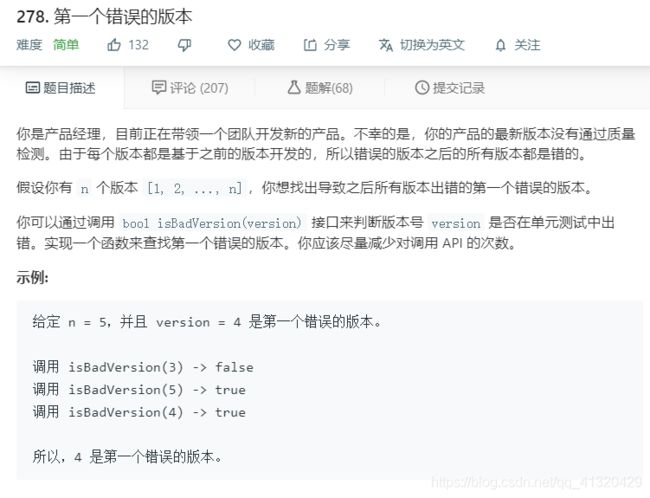
278.第一个错误的版本
边界就是第一个错误的版本,直接用模板一找左边界即可
可能会爆界,注意不要溢出
// Forward declaration of isBadVersion API.
bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int l=1,r=n;
while(l<r){
int mid =(long long)l+r>>1;
if(isBadVersion(mid))r=mid;
else l=mid+1;
}
return l;
}
};
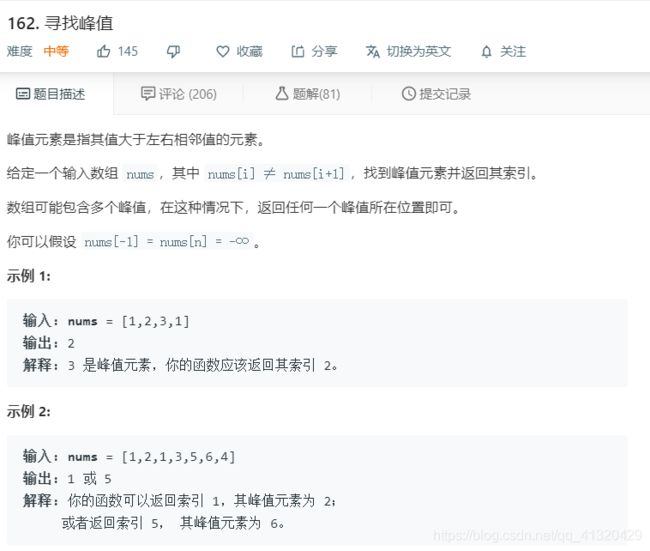
162.寻找峰值
思路:极大值两边的元素都满足小于峰峰值这个临界条件,所以在二分逼近时只需要确定更新的边界属于左右哪一边即可
这里假定mid为上升沿或下降沿的某一值,并用它与mid+1进行比较,从而确定更新区间
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int l=0,r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=nums[mid+1])r=mid; //确定处于上升沿还是下降沿
else l=mid+1; //循环内l和r不可能同时为n-1,所以不用考虑mid+1是否会溢出
}
return l;
}
};
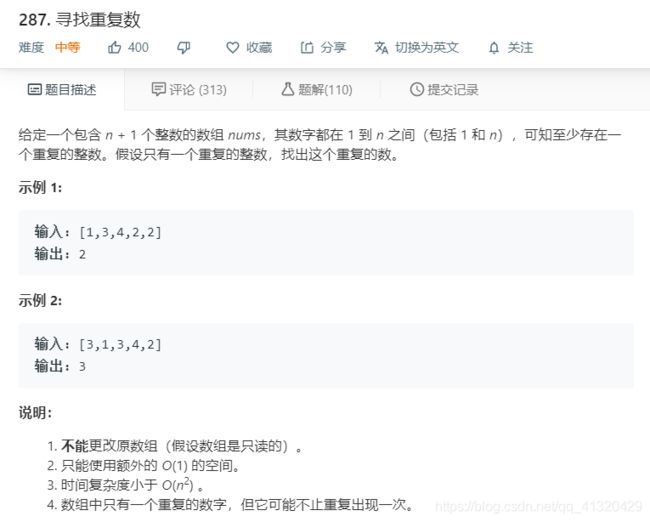
287.寻找重复数
题目分析:首先不能更改数组即不能排序
其次不能用额外的堆栈,时间复杂度小于平方即不能用简单遍历的方法
思路:
由抽屉原理知,该数组一定有某一个数数值重复
采用分治的思想,将每个数的取值的区间[1, n]划分成[1, n/2]和[n/2+1, n]两个子区间,然后分别统计两个区间中数的个数。
注意这里的区间是指 数的取值范围,而不是 数组下标,,本题我们对取值进行二分,而不是对下标进行二分
如果某个区间的数的统计个数超过了区间长,那么该区间一定有重复元素
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n=nums.size()-1;
int l=1,r=n; //数据范围1~n(二分范围)
while(l<r){
int mid=l+r>>1;
int cnt=0;
for(auto x:nums){ //例如mid=2,如果1~2范围的数超过了两个,那么说明重复的数一定存在于1~2中,再对1~2二分即可
if(x>=l&&x<=mid)
cnt++;
}
if(cnt>mid-l+1)r=mid;
else l=mid+1;
}
return l;
}
};
附上自己根据区间二分的代码
思路相似,统计时增加bool count 统计该元素是否出现过,出现过两次及以上则确定该元素所在的区间(有可能左右都有)
ps
后来发现好像只能用O(1)空间233这样确实多此一举了还不如一个for循环
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int l=0,r=nums.size()-1;
int n=nums.size();
int count[n];
for(int i=0;i<n;i++)count[i]=0;
while(l<r){
int mid=l+r>>1;
for(int i=0;i<=mid;i++){
if(count[nums[i]])r=mid; //如果在左区间出现过超过一次的元素,则重复元素在左区间,否则在右区间(不排除左右两区间都有)
count[nums[i]]++;
}
if(r!=mid)l=mid+1; //左区间没有,更新右区间
for(int i=0;i<n;i++)count[i]=0;
}
return nums[l];
}
};
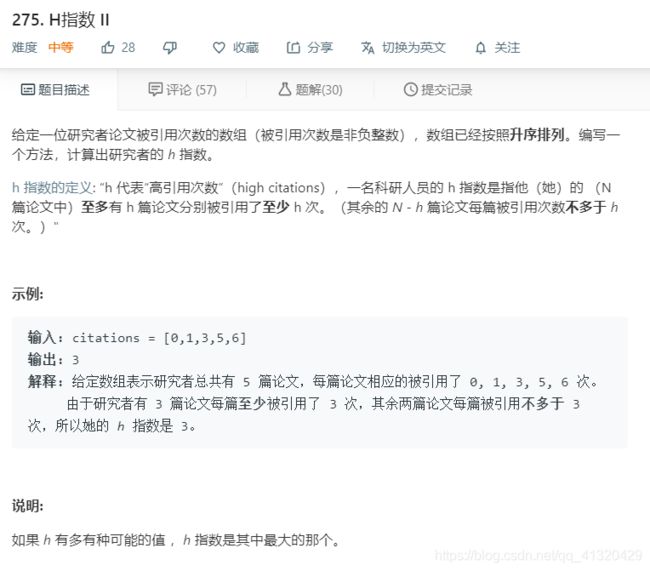
275.H指数II
题目翻译有点问题,改为至少有h篇论文分别被引用了至少h次
思路:
倘若说一个科研人员写了n篇论文,那么他的h最大只能为n
所以我们在0~h中进行二分
首先找到mid,如果说数组中有mid个数大于等于mid的话,mid就为当前找到的最大h,我们更新边界,尝试往更大的方向找,直到不满足条件为止
class Solution {
public:
int hIndex(vector<int>& citations) {
if(citations.empty())return NULL;
int n=citations.size();
int l=0,r=n;
while(l<r){
int mid=l+r+1>>1; //此题应用模板2
int cnt=0;
for(auto x:citations){
if(x>=mid)cnt++;
}
if(cnt>=mid)l=mid; //如果存在大于等于mid个数大于等于mid,说明h至少为mid大小,更新左边界
else r=mid-1;
}
return l;
}
};
下面是简化写法,上面方便理解
class Solution {
public:
int hIndex(vector<int>& citations) {
int n=citations.size();
int l=0,r=n;
while(l<r){
int mid=l+r+1>>1;
if(citations[citations.size()-mid]>=mid)l=mid; //倒数第mid个数大于等于mid,则有mid个数都大于等于mid
else r=mid-1;
}
return l;
}
};