信息学奥赛一本通 1282：最大子矩阵

【题目描述】

已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 × 1)子矩阵。

比如，如下4 × 4的矩阵

0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

的最大子矩阵是

9 2
-4 1
-1 8

这个子矩阵的大小是15。
【输入】

输入是一个N×N
的矩阵。输入的第一行给出N(0

【输出】

输出最大子矩阵的大小。
【输入样例】

4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

【输出样例】

15

解题思路：
在力扣上做了一题求最大子序和，对象是一维数组，用的是动态规划思想，很简单在这就不赘述了，题目和代码如下：

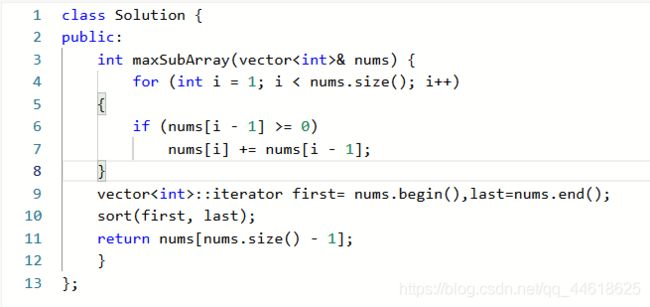
求二维数组的最大子矩阵其实和一维数组是一样的，把一维数组的a[i]看做是二维数组中第i列里某几行的和就行了。这个时候改变行数的上界和下界，相当于控制了行数不变，把二维数组变成了一维数组，再使用前面提供的求最大子序和函数，不需做任何改动，对其求最大值就解决了。上代码：

#include
#include
#include
using namespace std;
int maxSubArray(vector<int>& nums)//一维数组求最大子序列
{
    for (int i = 1; i < nums.size(); i++)
    {
        if (nums[i - 1] >= 0)
            nums[i] += nums[i - 1];
    }
    vector<int>::iterator first = nums.begin(), last = nums.end();
    sort(first, last);
    return nums[nums.size() - 1];
}
int main()
{
    int n;
    int arr[100][100];
    cin >> n;
    int max_ = 0;//最大子矩阵的和
    int a[100] = { 0 };
    for (int i = 0; i < n; i++)//存数组
    {
        for (int j = 0; j < n; j++)
            cin >> arr[i][j];
    }
    for (int i = 0; i < n; i++)//设定行的上界和下界，从第i行到第j行
    {
        for (int j = i; j < n; j++)
        {
            memset(a, 0, sizeof(a));
            for (int k = 0; k < n; k++)//将第i行到第j行的第k列求和，存入a[k]
            {
                for (int w =i; w <= j; w++)
                    a[k] += arr[w][k];
            }
            vector<int>tem(a,a+n);
            max_ = max(maxSubArray(tem), max_);
        }
    }
    cout<<max_;
    return 0;
}