r-net:machine reading comprehension with self-matching networks
文章目录
- 1.模型概述
- 2.passage和question编码层
- 3.Gated Attention-based RNN
- 4.Self-Matching Attention
- 5.output layer
- 6.源码和参数
- 参考链接
我觉得这篇文章的文笔真的有点不敢恭维,首先向量矩阵的维度不说清楚还能脑补,但是这边前后不同层之间用一样的变量名是什么意思啊(这么说出来会不会被MSRA鄙视,以后的简历都过不了了,ORZ),本文中尽量避免这种情况。嗯嗯,文章还是不错的^@^
标记版文章下载地址:zsweet github
原始文章下载地址:
Gated Self-Matching Networks for Reading Comprehension and Question Answering
R-NET: MACHINE READING COMPREHENSION WITH SELF-MATCHING NETWORKS
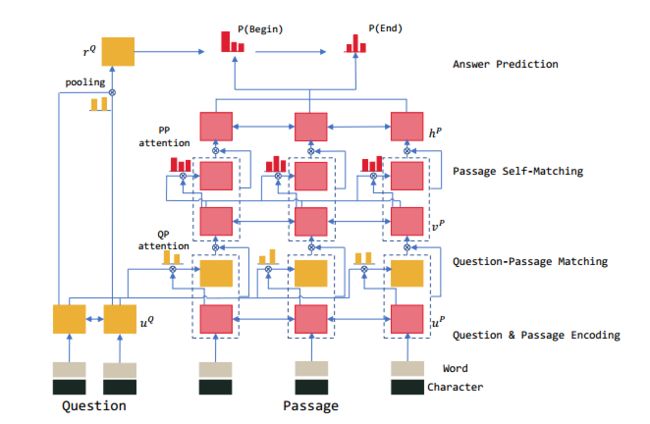
这里先总结下几个特点:
- 同时使用了char-embedding和word-embedding,不同的是char-embedding是通过将char放入双向gru之后,最终的是通过gru的最终状态来得到的。
- 在attention之后添加gate,主要用在Question-Passage Matching和Passage Self-Matching之后。
- 对文章本身进行self-attention。
1.模型概述
其实我觉得整体结构就是math-lstm和transformer模型的融合,然后再加了一点的小trick.
模型整体可以分为如下几个模块:
- embedding层
- RNN网络分别对question和passage单独编码 (本文中将前两部分放在一个部分介绍)
- 基于门限的注意力循环神经网络(gated-attention based recurrent network)匹配question和passage,获取问题的相关段落表示(question-aware passage representation)
- 基于自匹配注意力机制的循环神经网络(self-matching attention network),将passage和它自己匹配,从而实现整个段落的高效编码
- 基于指针网络(pointer-network)定位答案所在位置
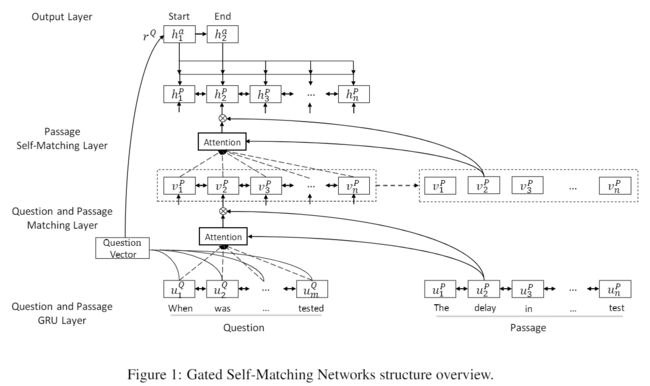
2.passage和question编码层
输入问题 Q = w t Q t = 1 m Q={w_t^Q}_{t=1}^m Q=wtQt=1m和段落 P = w t P t = 1 n P={w_t^P}_{t=1}^n P=wtPt=1n,分别进行word-level编码和character-level编码,得到向量 e e e和 c c c。这里character-level编码主要是为了应对OOV的影响,以往OOV词向量直接就是0,这里可以缓和OOV的影响。之后,利用两个双向RNN网络分别对question和passage再编码。而之前多数都是用的CNN卷积和highway。另外,作者在这里选用了GRU单元,而不是LSTM,原因在于GRU计算量更小。
u t Q = B i G R U ( u t − 1 Q , [ e t Q , c t Q ] ) \mathbf u_t^Q = \rm{BiGRU }(u_{t-1}^Q, [e_t^Q, c_t^Q]) utQ=BiGRU(ut−1Q,[etQ,ctQ])
u t P = B i G R U ( u t − 1 P , [ e t P , c t P ] ) \mathbf u_t^P = \rm{BiGRU }(u_{t-1}^P, [e_t^P, c_t^P]) utP=BiGRU(ut−1P,[etP,ctP])
其中: e t , c t e_t, c_t et,ct分别表示词向量和字向量,编码后的passage为 [ u 1 Q , u 2 Q . . . u m Q ] [u_1^Q,u_2^Q...u_m^Q] [u1Q,u2Q...umQ],query为 [ u 1 P , u 2 P . . . u n P ] [u_1^P,u_2^P...u_n^P] [u1P,u2P...unP]
3.Gated Attention-based RNN
首先对query做attention:
s j t = v T tanh ( W u Q u j Q + W u P u t P + W v P v t − 1 P ) , j = 1 , ⋯ , m s_j^t = v^T \tanh (W_u^Q\mathbf u_j^Q + W_u^P \mathbf u_t^P + W_v^P \mathbf v_{t-1}^P), \quad j = 1, \cdots, m sjt=vTtanh(WuQujQ+WuPutP+WvPvt−1P),j=1,⋯,m
α j t = s o f t m a x ( s j t ) \alpha_{j}^t = \rm{softmax}(s_j^t) αjt=softmax(sjt)
c t = ∑ i = 1 m α i t u i Q \mathbf c_t = \sum_{i=1}^m \alpha_i^t \mathbf u_i^Q ct=i=1∑mαituiQ
上述的attention可记为 c t = a t t n ( u Q , [ u t P , v t − 1 P ] ) 。 \mathbf c_t = \rm{attn}(\mathbf u^Q, [\mathbf u_t^P, \mathbf v_{t-1}^P])。 ct=attn(uQ,[utP,vt−1P])。
上面的attention与match-lstm一样,但是这里又增加了一个gate:
g t = s i g m o i d ( W g [ u t P , c t ] ) g_t = sigmoid(W_g[\mathbf u_t^P,\mathbf c_t]) gt=sigmoid(Wg[utP,ct])
[ u t P , c t ] ∗ = g t ⊙ [ u t P , c t ] [\mathbf u_t^P, \mathbf c_t]^* = g_t \odot [\mathbf u_t^P, \mathbf c_t] [utP,ct]∗=gt⊙[utP,ct]
然后再像match-lstm一样放入RNN:
v t P = B i G R U ( v t − 1 P , [ u t P , c t ] ∗ ) \mathbf v_t^P = \rm{BiGRU}(\mathbf v_{t-1}^P, [\mathbf u_t^P, \mathbf c_t]^*) vtP=BiGRU(vt−1P,[utP,ct]∗)
每个 v t P \mathbf v_t^P vtP动态地合并了来自整个Q的匹配信息。
可以看到,这一步骤和match-lstm的唯一区别就是增加了这个 g t g_t gt来控制passage和attention之后的query的输出量。
Gate RNN的门机制:
- 与GRU和LSTM不同
- 门机制是基于当前 P t P_t Pt和它的对应的 Q Q Q的注意力向量 c t c_t ct(包含当前pt和Q的关系)
- 模拟了阅读理解中,只有P的一部分才与问题相关的特点
其实这个gate我觉得是很像那个highway的,在transformer里面用的是residual,但是这里和下面的self-attention之后换成了伪highway,甚至我觉得这个地方换成residual也未必不好,但是我没尝试过。
4.Self-Matching Attention
为了充分利用Passage的上下文信息。增加对passage的self-attention :
s j t = v T tanh ( W v P v j P + W v P ˉ v t P ) , j = 1 , ⋯ , n s_j^t = v^T \tanh (W_v^P \mathbf v_j^P + W_v^{\bar P} \mathbf v_t^P), \quad j = 1, \cdots, n sjt=vTtanh(WvPvjP+WvPˉvtP),j=1,⋯,n
β j t = s o f t m a x ( s j t ) \beta_{j}^t = \rm{softmax}(s_j^t) βjt=softmax(sjt)
d t = ∑ i = 1 n β i t v i P \mathbf d_t = \sum_{i=1}^n \beta_i^t \mathbf v_i^P dt=i=1∑nβitviP
上述的attention可记为 d t = a t t ( v P , v t P ) \mathbf d_t = att(v^P,v_t^P) dt=att(vP,vtP))
同样在这里添加gate:
g t ′ = s i g m o i d ( W g [ v t P , d t ] ) g'_t = sigmoid(W_g[\mathbf v_t^P,\mathbf d_t]) gt′=sigmoid(Wg[vtP,dt])
[ v t P , d t ] ∗ = g t ′ ⊙ [ v t P , d t ] [\mathbf v_t^P, \mathbf d_t]^* = g'_t \odot [\mathbf v_t^P, \mathbf d_t] [vtP,dt]∗=gt′⊙[vtP,dt]
同样放入RNN计算:
h t P = B i G R U ( h t − 1 P , [ v t P , d t ] ∗ ) \mathbf h_t^P = \rm{BiGRU}(\mathbf h_{t-1}^P, [\mathbf v_t^P, \mathbf d_t]^*) htP=BiGRU(ht−1P,[vtP,dt]∗)
Self-Matching根据当前p单词,从整个Passage中提取信息。最终得到Passage的表达 H P H^P HP。
我奇怪的是这里在计算 s j t s_j^t sjt的时候为什么没有使用RNN中t-1时刻的输出 h t − 1 P h_{t-1}^P ht−1P?难道效果不好?
5.output layer
类似于match-lstm中的最后输出层Ptr-net:
计算 t t t时刻的attention-pooling passage (注意力 c t \mathbf c_t ct)
s j t = v T tanh ( W h P h j P + W h a h t − 1 a ) s_j^t = \mathbf v^T \tanh(W_h^P\mathbf h_j^P + W_h^a \mathbf h_{t-1}^a) sjt=vTtanh(WhPhjP+Whaht−1a)
γ i t = s o f t m a x ( s j t ) \gamma _i^t = \rm{softmax}(s_j^t) γit=softmax(sjt)
f t = ∑ i = 1 n γ i t h i P \mathbf f_t = \sum_{i=1}^n \gamma_i^t \mathbf h_i^P ft=i=1∑nγithiP
p t = arg max i ( γ i t ) p^t = \arg \max_{i}(\gamma_i^t) pt=argimax(γit)
上述的attention可记为 f t = a t t ( h P , h t − 1 ) \mathbf f_t = att(h^P,h_{t-1}) ft=att(hP,ht−1)
RNN前向计算
h t a = G R U ( h t − 1 a , f t ) \mathbf h_t^a = \rm{GRU} (\mathbf h_{t-1}^a, \mathbf f_t) hta=GRU(ht−1a,ft)
基于注意力权值去选择位置。
上面的这是match-lstm中的Ptr,在R-net中是增加了RNN中的初始状态初始化,
初始hidden state是Question的attention-pooling vector:
h 0 Q = r Q \mathbf h_{0}^Q = \mathbf r^Q h0Q=rQ
基于Q的编码和一组参数 V r Q V_r^Q VrQ,利用注意力机制计算 r Q \mathbf r^Q rQ
s j = v T tanh ( W u Q u j Q + W v Q V r Q ) , j = 1 , ⋯ , m s_j = \mathbf v^T \tanh(W_u^Q \mathbf u_j^Q + W_v^Q V_r^Q), \quad j = 1, \cdots, m sj=vTtanh(WuQujQ+WvQVrQ),j=1,⋯,m
δ i = s o f t m a x ( s i ) \delta_i = \rm{softmax}(s_i) δi=softmax(si)
r Q = ∑ i = 1 m δ i u i Q \mathbf r^Q = \sum_{i=1}^m\delta_i \mathbf u_i^Q rQ=i=1∑mδiuiQ
上述的attention可记为 r Q = a t t n ( u Q , V r Q ) \mathbf r^Q = \rm{attn}(\mathbf u^Q, \mathbf V_r^Q) rQ=attn(uQ,VrQ)
同样这里有点奇怪的是,按说这里的 V r Q V_r^Q VrQ是一个向量的,并且 W v Q V r Q W_v^Q V_r^Q WvQVrQ也是个向量,这不就相当于一个bias向量吗?为什么写的这么麻烦?
之后从网上看到这个:
这里肯定会有很多人困惑这个V_r^Q是怎么来的,文中并没有介绍,其实它是RNN的首状态,大部分RNN的第一个输入都是这么处理的。看代码还会发现它就是一个通过tf.contrib.layers.xavier_initializer()初始化的参数,那为什么不把这个乘法写成一个参数呢,因为两个都是可学习的参数完全可以合并,我觉得是因为要和attention的输入保持一致(attention函数有两个输入)。
所以按照match-lstm中boundary方案,每次 f t = a t t ( h P , h t − 1 ) \mathbf f_t = att(h^P,h_{t-1}) ft=att(hP,ht−1)产生的权重就可以作为start-probability和end-probability了
目标函数:
− ∑ n = 1 N log p ( a n ∣ P n , Q n ) - \sum_{n=1}^N \log p(\mathbf a_n \mid P_n, Q_n) −n=1∑Nlogp(an∣Pn,Qn)
本文用的是边界模型,所以不用预测完整的序列,只预测开始和结束位置就可以了。
p ( a ∣ H r ) = p ( a s ∣ H r ) ⋅ p ( a e ∣ a s , H r ) p(\mathbf a \mid H^r) = p(a_s \mid H^r) \cdot p(a_e \mid a_s, H^r) p(a∣Hr)=p(as∣Hr)⋅p(ae∣as,Hr)
6.源码和参数
模型细节:
- 训练集80%,验证集10%,测试10%
- 分词用的斯坦福的CoreNLP中的tokenizer
- 预训练好的Glove Vectors。训练中保持不变。
- 单层的双向GRU,末尾隐状态作为该单词的字符向量
- BiRNN编码Question和Passage中使用3层的双向GRU
- Hidden Size大小,所有都是75
- 每层之间的DropOut比例是0.2
- 优化器使用AdaDelta。初始学习率为1,衰减率β=0.95,ϵ=1e−6
-
r-net
该源码与原文比较贴合,readme和issue中没有提到过结果怎么样 -
zsweet github
这份源码提供了score,但是代码中没有完全按照r-net,因为拟合RNN实在太慢了,所以我研究的也是这份代码,区别就在attention上面,用的是transformer里面的那种attention,速度还是可以的。
原文中还提了很多的尝试,其中有个sentence rank的,之前我也在Dureader里面尝试过,尝试的是passage rank,效果也不好,其他的尝试可以参考文章,别人踩过的坑还是不要再踩一次了,当然这只是针对SQuAD
参考链接
- R-Net (Gated Self-Matching Networks)
- R-Net – Machine Reading Comprehension with Self-Matching Networks
- R-NET机器阅读理解(原理解析)
- 论文分享 - R-Net: Machine Reading Comprehension with Self-Matching Networks