Diary Ⅳ

2019/11/04

1.洛谷P3879 阅读理解
2.WOJ#1830
3.WOJ#4786 正解
4.1102考试T3【√】

1. 写法
2. 状态定义

做了一上午水题？

WOJ#2604 军队调遣
重载小于符号的时候反了（反正你记不到，每次就试一下）
两个板子（tarjan+最短路）

WOJ#1436 冰壶游戏
sb搜索
（可以迭代加深，效率显然更优）

WOJ#1814 文化之旅
启发式搜索
用set判断一下种类是否冲突

WOJ#1692 因子的排列
直接爆搜？？（由于要考虑很多细节，就直接贴std了）
统计排列数的时候有个技巧
由于我们是枚举当前这个质因数选的个数（有种累加的思想）
$s2=s2\ast (LDB)(y+i)/i;$
令S2为上一次的排列数，y为上一次选择的质因数的总个数
i从1开始枚举，表示当前这个质因数选的个数

WOJ#4577 山贼集团
不知道哪里来的执念，一定不要看题解
以至于到了现在，仍然没A……
下午再好好想想

剩下这两周：
1.图论
2.动态规划
3.数论
4.字符串
5.以前的考试题
6.杂题
7.NOIp真题

今天下午：
1.1102考试T3【√】+WOJ#4378 【2018提高测试】玩具【×】（晚上问一下lsr）
2.WOJ#4577 山贼集团【√】
3.tarjan复习（起码两道题）

WOJ#4577 山贼集团
呜呜哇哇┭┮﹏┭┮我以前还做过啊！！
现在自己yy，本来复杂度就是错的，顶多算个暴力，，，然后暴力也写挂了呜呜呜呜呜
（hou神说我没学过树上背包）
定义$f[u][status]$ 表示在以$u$为根的子树中，分配status的集团能获得的最大利益
考虑从子树转移来信息，不需要将status代到dfs中去
每次处理的时候就把所有情况处理完
儿子信息根据需要直接调用即可

POJ #3694 Network
找桥，缩点，建树，LCA，并查集

POJ#2942 knight of the round table
补图
性质:奇环
不能把割点拎出来然后跑dfs求$v-dcc$！！！！！！【×】
举个栗子：

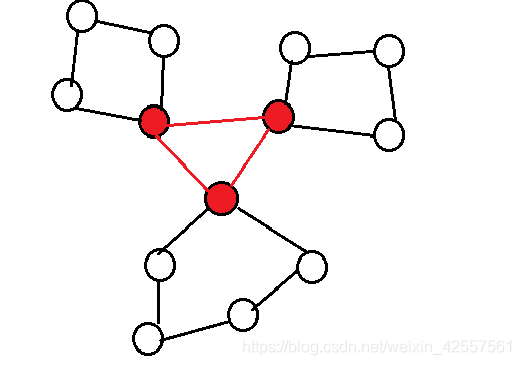
这样的情况如果dfs，就不能找到中间的那个$v-dcc$

所以呀，就好好地在tarjan里面求嘛~

		if(!dfn[y]){
			tarjan(y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x]){
				flag++;
				if(rt!=x||flag>1) cut[x]=1;
				int z;num++;
				do{
					z=stk[top];top--;
					dcc[num].push_back(z);
				}while(z!=y);
				dcc[num].push_back(x);//一个割点可以属于多个v-dcc 
			}
		}
		else low[x]=min(low[x],dfn[y]);

2019/11/05

昨天好废啊……现在只剩了不到两周了
姑娘你浪费不起了
一定要专注！
任务：
1.POJ2942【√】
2.仙人掌
3.考试题【√】
4.WOJ4750【√】
5.观光公交
6.ldx一道
7.总结

今天考试：
T1 85pts
T2 0pts
T3 20pts
Total:105pts
最高:160pts

T1 模拟
好坑啊……对方是负值的时候直接打没有打他优

T2 MST+组合数
数据范围，记得开long long
掉了10pts暴力

hxy好强
考场推出正解

我也发现是MST了啊。。只是太菜了没有和这道题联系在一起
当前求出来的MST的边权和假设为sum
如果$sum>X$ ，显然无解
如果$sum<X$，我们就假设把当前的最小生成树的边都染成同一种颜色，考虑加入一条另外颜色的边。如果加入新边后（相当于求次小生成树）$su{m}^{\prime }==X$ ，那这条边是我们可以选的，计入cnt1中。如果$su{m}^{\prime }>X$，说明这条边对答案无影响，计入cnt2中。如果$su{m}^{\prime }<X$，那么当前这条边必须和最小生成树染成一种颜色。那么在这种情况下的答案就是$$2\ast (2^{cnt1}-1)\ast 2^{cnt2}$$
对于$sum==X$ 的情况类似讨论即可

T3
一眼数位dp
结果人家重点是字符串匹配
KMP自动机上dp

gigo好棒☆(￣▽￣)/$:*
考场推出正解【鼓掌！】
update：被Hack了。复杂度是假的。（不碍事儿，能A就是好算法）

大致理一下这个思路吧（还是很清楚的）
你想啊，给定的长串，如果为它建一个Trie树
是问号的地方就相当于有0~9的儿子
那如果（假设我们现在在遍历Trie树）我们知道当前这个节点的子树size（也就是合法方案数），那我们是不是就可以很简单地处理出第k大了呀
问题转化到这里已经解决一大半了
现在考虑如何预处理出当前这个节点的子树信息
首先：

1.我们该如何确定这个节点？
显然位于原串的第$i$位，这个信息必须要有
但只有这个信息还不够，假设当前第i位之前有很多 ‘ ? ’
那每一个问号对应走到的节点是不一样的，再记一个与短串匹配的位数
所以我们用$f[i][j]$来表示一个节点（不能显式建树，5e4个节点，10^5e4）

2.$f[i][j]$表示a串处理到第i位，匹配了b串的j位，i+1~n合法的填数方案。初值：$f[n][m]$=1
由于处理第i+1位的时候，j的变化可能不是j+1，这时候我们需要维护一个类似kmp的next数组
定义$fail[i][k]$表示当前在第i位，下一位填k的最长公共前后缀
转移就是：$f[i][j]+=f[i+1][fail[j][k]]$
3.处理完这些后我们终于可以开始考虑询问了。奈何询问1e5，如果每次都从根节点一直找，那就是nq的了。考虑离线（结果还是会被卡，还是STD的办法好，倍增来找）

2019/11/06

好多好多天都没有认真按照计划来执行了
今天一定不能再被分心了，合理安排计划！

今天考试
严重怀疑我们做的是NOI的题。。L可能为了不打击我们的自信心，连成绩都没有发(嘤嘤嘤，菜到真实)
T1：莫比乌斯反演+杜教筛
T2：思维好题
T3：状压dp+矩阵快速幂优化

得嘞。。直接弃疗

11：40~12：15 昨天的总结【√】
12：15~13：05 吃饭+休息
13：05~13：30 中等的字符串暴力+正解【√】（15：30）
任务：

• Cf L. Timsort
• 考试题T2
• Cf B. Dev, Please Add This!
• Cf A. Coloring Roads
• WOJ4799 异或的做法

WOJ#4750 中等的字符串
首先，暴力不会。
将所有的串建在AC自动机上，然后类似树形dp
$f[x][dep]$表示走了dep步，当前在x这个节点所得到的最高得分
记忆化搜索即可

考虑优化
这个范围10¹²，一看就不能傻傻地直接走那么多步
由于我们每次的决策空间是一样的，我们就可以矩阵快速幂优化了

Cf L. Timsort
细节打挂……果然没有想清楚的地方，瞒谁都瞒不过数据
一开始就觉得自己末尾那个地方没有处理清楚（果然，不能轻易放过自己的思维漏洞）
不过整体的思路是自己想出来的还是不错

WOJ#4799 我的订书机之恋
妙极了。。只可意会不可言传

2019/11/07

上午任务

• Cf B. Dev, Please Add This!
• Cf A. Coloring Roads
• WOJ#4799 异或的做法
• WOJ#1829 聪明的质检员
• WOJ#3210 序列生成

WOJ#1829 聪明的质检员
yeah，开心(*^▽^*)
自己yy出来啦~~
只是。。又和昨天一样，细节打挂（由于随着w的增大，答案在递减，所以最后比较的肯定是ans和ans+1）

Cf B. Dev, Please Add This!
建图没有想错，只是怎样建图很关键

把两个’#'中间的部分看做一个分量
那么对于‘*’来说，至少得有一个分量（横/纵）被到达 　　-----限制①
对于任意一个分量，如果Ball不能到达，则一定不能选择 　　-----限制②
对于任意两个分量，如果不能互相到达，则一定不能同时选择 　　-----限制③

这些限制，我们该如何建边呢？其实就是一个2-SAT问题
我们将一个分量看做两个点（0/1），0表示不能到达，1表示可以到达
那么限制①，设这两个分量为idx1,idx2 。那么就是(idx1,0)–>(idx2,1)以及(idx2,0)–>(idx1,1)
限制②就是(ball,1)–>(idx,0)（事实上在代码实现的时候，我们将不能到达的点，(idx1,1)–>(idx1,0)）
限制③(idx1,1)–>(idx2,0)以及(idx2,1)–>(idx1,0)

最后Tarjan缩点，如果一个分量的两个点在同一个联通块里，显然矛盾

Cf A. Coloring Roads
一些基础的知识不扎实
树链剖分时由于每次都先搜索重儿子，那么每条重链上的DFS序就是连续的。每条边的信息都存在这条边深度较大的儿子上。
这道题据说做法很多
我选了一个看起来比较友好的做法：树链剖分+单调栈。对于每条重链维护一个关于DFS序的单调递减栈从而维护答案，每次暴力修改，均摊分析复杂度是对的【看起来就像一个可爱的暴力】（每个询问最多被加入一次，删除一次）

WOJ#3210 序列生成
没有怎么理解AC自动机的内涵
实际上，它就是告诉你你的转移往哪里去呀
然后就很简单了
数位dp+AC自动机
（注意前导0！！！）

下午任务
把NOIp真题做完（大部分都是简单题了）

WOJ#1844 Hankson 的趣味题
自己yy了一个做法，复杂度没问题
但是没写出来？？？最近代码能力是怎么了？？
总是想到正解，却写不出来
（难道是因为之前直接粘代码的报应？oh，我要做好码奴）

不需要分开存在数组里，一起分解质因数就好了
不然你要分别存下来，光是memset就把时间卡满了
对于>50000的质因数特殊判断一下即可
这个特判不简单啊……
假设最后剩下了$a0,a1,b0,b1$
首先肯定a0==a1&&b0==b1
如果$a0!=b0\&\&a0==1$ ans<<=1
否则无解

WOJ#1830 观光公交

引自博客
从部分分推正解

按照我自己yy的dp来说，没有理解题目要求最优化的到底是什么
： 是旅客的旅行时间总和最小
但是dp只解决了到达当前这个点的最小时间
而这个贪心就很妙了啊~由于加速器那我们每次选择能惠及人数最多的加速一定最优（每使用一次加速器，对于乘客而言都只能减少1，所以最大化人数即可）

• 顺序（应该是先取前面的）
• dp（也可以试着换一种方式定义，最优化总时间）

2019/11/08

今天考试
（心态爆炸？？不不不，没有没有，我没有爆炸，只是没有调整好考试策略，积累一下）
T1 100pts
T2 100pts
T3 0pts

T1 8:00~9:00
样例有毒吧。。复制出来少最后一位
调死我了……最后过了样例就没管了
直接用文件读入

我好像又是伪算法，，直接找规律？？
可以证明我通项公式的正确性
推一波双胞胎式子（对称性）
然后等比数列转化一下

事实上也是很套路的一道题了
由于给定的式子$p_i=a\ast p_{i-1}+b\ast p_i+c\ast p_{i+1}$
我们一看就长得像递推的式子，但如果直接这样看，会发现i与i-1和i+1有关，这怎么搞……
显然啊，把i+1挪到一边
得到$c\ast p_{i+1}=(a+c)\ast p_i-a\ast p_{i-1}$
这样的话，要是我们知道$p0$和$p1$不就随便做了嘛
可是我们知道的是$p_0$和$p_{2n}$
仔细思考一下，会发现$p2=()\ast p1+()\ast p0$
然后p0==0所以$p2=()\ast p1$
然后就会发现，任意一个$p_i$都可以用$p_1$来表示
做完啦

实际上还可以用矩阵快速幂优化一波

T2 9:30~11:30
细节差一点又处理挂，最后一分钟才找到问题…
读题啊。。。。
把每个细节记在草稿本上或者Highlight，写完程序后返过去检查一下。细节是否处理到位

据说暴力好像均摊复杂度是正确的？？

T3 我凉了
根本没看题

据说也是一道不可做题？？
emmm……

任务：

• 学习每道题的正解
• 观光公交dp（无做法）
• 模拟旅行

WOJ#4490 「GXOI / GZOI2019」旅行者
多源最短路+二进制分组
（mark没有清空，出现了无数多的错误情况。一定要想清楚是否需要清空）

注意:

for(re int i=e[u].size()-1;i>=0;--i)

这样写是不对的，因为STL的size都是存在unsigned 里的
而unsigned是无符号，如果sze=0，然后一减，就会变成极大值

数组清空！！！

根据需要清空数组。不能每次memset都把定义的所有清空（那复杂度不是卡满了的O(n)嘛）

memset(dis,127,sizeof(ll)*(n+2));

第一个括号是数据类型，第二个是需要清空的大小

贪婪大陆
T2异或

2019/11/09

今天校庆考试
完全不在状态。。T2伪算法打挂，然后最尴尬的是分段考虑的情况$n\le 200$写的居然是$N\le 200$
话说我还检查了啊……果然状态不对的时候强迫自己检查是没有任何用处的。。
今天中午的时候和rich浪，没有睡觉
废了一下午，我死了
下午回家的时候先睡了一觉，然后吃了个饭
感觉好点了，不容易走神了
理一理任务吧：
今天的T2，T3
贪婪大陆

T1 100pts
T2 20pts
T3 0
Total：120pts
最高：204pts

T1 背包
T2
假结论就不说了

正解：
从优化n³的暴力开始
其实我们不需要枚举每一个可能的根节点，只要有一个可能的根节点出现，如果它递归下去的子树不满足条件，则一定不满足条件

这是一个结论：题目中给定的序列合法的充要条件是对于任意一个区间，都存在一个数使得这个数与区间其他数的差的绝对值不超过 k。
然后就变成n²啦
我们如果从 l, r 同时向中间找，也就是第 t 步判断 l + t 和 r-t 是否是合法的 i，那么时间复杂度变成了
T(n) = T(k) + T(n k 1) + min{O(k), O(n k)} = O(n log n)，

T3
完全不知道如何下手。
考虑现在在每一个交点的地方我们都对向交换，那么最后得到的顺序一定正确，这就是最多的对向交换次数（交点数）
那么最少的对向交换次数呢？
由于没有学过群论，目前还不知道为什么是n-置换数

2019/11/10

1. 昨天考试T3
   写了好久好久……
   1 . 线段树区间加居然写挂了！！！！。儿子节点更新的时候用的是$seg[k].tag$，我个zz居然写的是$seg[k].val$
   2 . 数组开小
2. T2的异或
3. 贪婪大陆
4. NOip真题
5. 周末作业
6. 下周计划（模板复习计划）