博弈论--例题杂烩

感谢这位不知名的dalao
以下内容大多摘自这个链接。
标有黄色高亮的才是Xly著
（尊重版权，人人有责）
不贴代码，只是因为太占篇幅

（一）考虑奇偶性的变化

例题hdu1079 Calendar Game
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1079

题意：从当前日期开始，玩家可以选择移动到下一天或者下一个月的同一天（如果月份加1超过12，则进入新的一年；如果移动使得新的日期不合法，则不能移动）。如果一个玩家移动到2001年11月4日，则该玩家胜利；如果一个玩家移动到2001年11月4日以后，则该玩家失败，问先手必胜还是后手必胜。

分析：我们发现，进行一次移动后，日期与月份之和的奇偶性总发生改变（除了9月30日和11月30日）。那么，如果不考虑这两天的情况下，如果初始日期月份与日期之和为偶数，则先手必胜。如果初始日期为9月30日或者11月30日，先手可以选择奇偶性不变的一次日期变化。这样就又成了先手必胜的情况。下面我们考虑是否中间会遇到这两个特殊点。如果初始状态为先手必胜，则先手总存在办法，不到达这个两个特殊点，即（8月30日和10月30日时不选择增加月份，9月29日和11月29日时不选择日期）。如果初始状态为先手必败，同样，后手总有办法不到达这两个特殊点。所以只可能在初始时除于这两个特殊点。即，读入日期后，我们判断日期与月份之和为偶数或为9月30日或为11月30日，先手必胜；否则，后手必胜。

做题思路：首先画出有向图游戏，很明显的发现这是一个间隔式胜负，那我们的任务就是将日期与某种运算（方法）统一起来，形成一种映射，进行判断。发现每次转移，日期与月份之和的奇偶性一定会改变，恰好每次转移胜负也会发生改变，这样就可以对应起来了。然而有特殊情况，9月30日和11月30日，无论怎样移动，都不会改变奇偶性。特判一下即可。

SG函数
本来以为此题SG不可做，后来看了dalao博客，才知道SG函数的正确打开方式
定义一个三维数组，年、月、日
然后注意细节，从后往前转移即可

例题 hdu1564 Play a game（大大大大大水题）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1564

题意：给你一个n*n的棋盘，游戏开始时有一块在拐角处的石子。两个玩家轮流移动该石子，移动时只能移动到相邻且未访问过的点，问先手必胜还是后手必胜。

分析：我们对该棋盘用$1\ast 2$的长方形进行覆盖。若n为偶数，那么必存在一个覆盖方案。此时先手选择走向与当前状态同处一个长方形内的另一点。这样，无论先手怎么移动，先手必存在一种移动方法。由于这个游戏无平局，所以先手必胜。若n为奇数，我们考虑同样的方法，将$n\ast n$的棋盘除去起点的$n\ast n-1$格进行覆盖。之后无论先手怎么走，后手都存在一种移动方案，所以先手必败

例题 hdu4203 Doubloon Game（证明存疑）

题意：有n枚硬币，再给你一个数k，每次只能拿k^m枚（m为自然数），两人轮流拿，先拿完者胜。如果先手必败，输出0，否则输出先手保证必胜的情况下第一步最少拿的硬币数。

分析：先考虑k为奇数的情况，此时k的m次方一定为奇数。也就是说，如果n为奇数，那么最后一枚硬币一定是先手拿的，且第一轮只用拿1枚即可。若n为偶数，则先手必败。然后再考虑k为偶数的情况，首先我们可以手算出n=0,1,0,1,```,0,1,k。之后接下来用数学归纳法证明其周期为(k+1)。

实际情况：根本想不出来要推算k的奇偶性，这时候就应该借用SG函数打表找规律了（然而第一次写SG函数就写炸了( ⊙o⊙））

例题 bzoj2927 多边形之战

题目：给定一个凸多边形的三角剖分，其中一个三角形被涂成了黑色，每次可以一刀割下一个三角形，割下黑色三角形的人胜利。

分析：建立其对偶图，问题转化为一颗树上有一个黑色节点，每次删去一个叶节点，删去黑色叶节点的人胜利。如果一开始黑色节点就是叶节点，那么先手必胜。其他情况，黑色点必须剩两个白点连在其旁边保证它不为叶节点，否则对方必胜。由于每次只能删去一个叶节点，这种情况下，胜负就只与n的奇偶性相关了。

开心模拟：
做了这么些博弈了，突然脑抽，我怎么知道那个玩游戏的人怎么操作啊？玩游戏的人怎么知道怎么操作最优啊？既然游戏一开始就知道胜负了，还玩什么玩？？？比如，面对这道题，那么多三角形 我怎么知道切哪一个？？？

zxy神仙白了我一眼“你tm不知道从后往前推？”

既然三角形太多我们就从简单的下手，下面这张图也就很显然了
（按照上面的做法，我们将三角形看做一个个的点来进行分析。N是必胜局面，P是必败局面。必胜、必败均是对当前局面的先手而言）

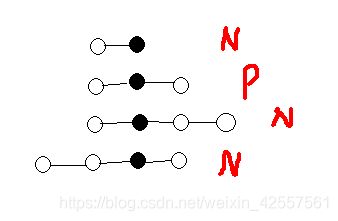
这样一分析，结论也就很显然了
当n为奇数的时候，必败；反之必胜
特殊情况就是如果一开始黑色的三角形就在最外面，那么直接胜利