【LeetCode】28.实现strstr() (KMP超详细讲解,sunday解法等五种方法,java实现)
题目
链接
分析
概述
这道题是要在 haystack 字符串中找到 needle 字符串。下面会给出的三种解法,这三种解法都基于滑动窗口。
子串逐一比较的解法最简单,将长度为 L 的滑动窗口沿着 haystack 字符串逐步移动,并将窗口内的子串与 needle 字符串相比较,时间复杂度为 O((N - L)L)
显示上面这个方法是可以优化的。双指针方法虽然也是线性时间复杂度,不过它可以避免比较所有的子串,因此最优情况下的时间复杂度为 O(N),但最坏情况下的时间复杂度依然为 O((N - L)L)。
有 O(N)复杂度的解法嘛?答案是有的,有两种方法可以实现:
- Rabin-Karp,通过哈希算法实现常数时间窗口内字符串比较。
- 比特位操作,通过比特掩码来实现常数时间窗口内字符串比较。
方法一:子串逐一比较 - 线性时间复杂度
最直接的方法 - 沿着字符换逐步移动滑动窗口,将窗口内的子串与 needle 字符串比较。
![]()
实现
class Solution {
public int strStr(String haystack, String needle) {
int L = needle.length(), n = haystack.length();
for (int start = 0; start < n - L + 1; ++start) {
if (haystack.substring(start, start + L).equals(needle)) {
return start;
}
}
return -1;
}
}
复杂度分析
- 时间复杂度:O((N - L)L),其中 N 为 haystack 字符串的长度,L 为 needle 字符串的长度。内循环中比较字符串的复杂度为 L,总共需要比较 (N - L) 次。
- 空间复杂度:O(1)。
方法二:双指针 - 线性时间复杂度
上一个方法的缺陷是会将 haystack 所有长度为 L 的子串都与 needle 字符串比较,实际上是不需要这么做的。
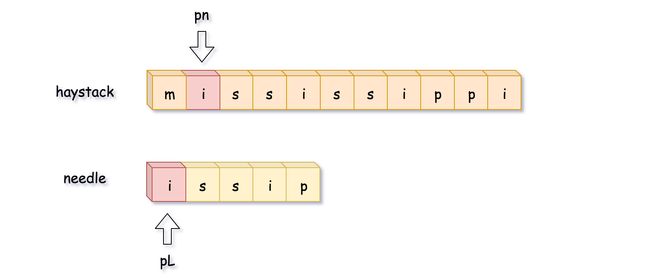
首先,只有子串的第一个字符跟 needle 字符串第一个字符相同的时候才需要比较。
其次,可以一个字符一个字符比较,一旦不匹配了就立刻终止。
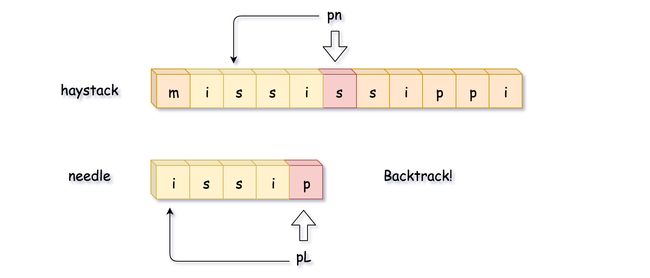
如下图所示,比较到最后一位时发现不匹配,这时候开始回溯。需要注意的是,pn 指针是移动到 pn = pn - curr_len + 1 的位置,而 不是 pn = pn - curr_len 的位置。
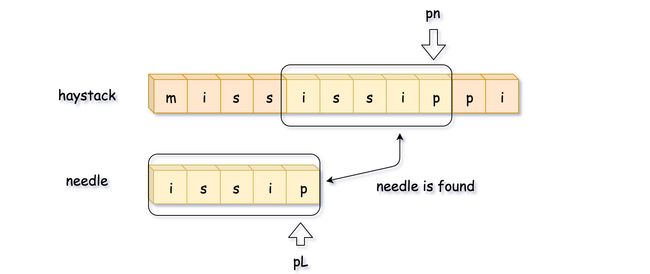
这时候再比较一次,就找到了完整匹配的子串,直接返回子串的开始位置 pn - L。
算法
- 移动 pn 指针,直到 pn 所指向位置的字符与 needle 字符串第一个字符相等。
- 通过 pn,pL,curr_len 计算匹配长度。
- 如果完全匹配(即 curr_len == L),返回匹配子串的起始坐标(即 pn - L)。
- 如果不完全匹配,回溯。使 pn = pn - curr_len + 1, pL = 0, curr_len = 0。
实现
class Solution {
public int strStr(String haystack, String needle) {
int L = needle.length(), n = haystack.length();
if (L == 0) return 0;
int pn = 0;
while (pn < n - L + 1) {
// find the position of the first needle character
// in the haystack string
while (pn < n - L + 1 && haystack.charAt(pn) != needle.charAt(0)) ++pn;
// compute the max match string
int currLen = 0, pL = 0;
while (pL < L && pn < n && haystack.charAt(pn) == needle.charAt(pL)) {
++pn;
++pL;
++currLen;
}
// if the whole needle string is found,
// return its start position
if (currLen == L) return pn - L;
// otherwise, backtrack
pn = pn - currLen + 1;
}
return -1;
}
}
复杂度分析
- 时间复杂度:最坏时间复杂度为 O((N - L)L),最优时间复杂度为 O(N)。
- 空间复杂度:O(1)。
方法三: Rabin Karp - 常数复杂度
有一种最坏时间复杂度也为 O(N)的算法。思路是这样的,先生成窗口内子串的哈希码,然后再跟 needle 字符串的哈希码做比较。
这个思路有一个问题需要解决,如何在常数时间生成子串的哈希码?
滚动哈希:常数时间生成哈希码
生成一个长度为 L 数组的哈希码,需要 O(L)时间。
如何在常数时间生成滑动窗口数组的哈希码?利用滑动窗口的特性,每次滑动都有一个元素进,一个出。
由于只会出现小写的英文字母,因此可以将字符串转化成值为 0 到 25 的整数数组: arr[i] = (int)S.charAt(i) - (int)'a'。按照这种规则,abcd 整数数组形式就是 [0, 1, 2, 3],转换公式如下所示。
h 0 = 0 × 2 6 3 + 1 × 2 6 2 + 2 × 2 6 1 + 3 × 2 6 0 h_0 = 0 \times 26^3 + 1 \times 26^2 + 2 \times 26^1 + 3 \times 26^0 h0=0×263+1×262+2×261+3×260
可以将上面的公式写成通式,如下所示。其中 c_ic**i 为整数数组中的元素,a = 26a=26,其为字符集的个数。
h 0 = c 0 a L − 1 + c 1 a L − 2 + . . . + c i a L − 1 − i + . . . + c L − 1 a 1 + c L a 0 0 h_0 = c_0 a^{L - 1} + c_1 a^{L - 2} + ... + c_i a^{L - 1 - i} + ... + c_{L - 1} a^1 + c_L a^00 h0=c0aL−1+c1aL−2+...+ciaL−1−i+...+cL−1a1+cLa00
h 0 = ∑ i = 0 L − 1 c i a L − 1 − i h_0 = \sum_{i = 0}^{L - 1}{c_i a^{L - 1 - i}} h0=∑i=0L−1ciaL−1−i
下面来考虑窗口从 abcd 滑动到 bcde 的情况。这时候整数形式数组从 [0, 1, 2, 3] 变成了 [1, 2, 3, 4],数组最左边的 0 被移除,同时最右边新添了 4。滑动后数组的哈希值可以根据滑动前数组的哈希值来计算,计算公式如下所示。
h 1 = ( h 0 − 0 × 2 6 3 ) × 26 + 4 × 2 6 0 h_1 = (h_0 - 0 \times 26^3) \times 26 + 4 \times 26^0 h1=(h0−0×263)×26+4×260
写成通式如下所示。
h 1 = ( h 0 a − c 0 a L ) + c L + 1 h_1 = (h_0 a - c_0 a^L) + c_{L + 1} h1=(h0a−c0aL)+cL+1
如何避免溢出
a^La**L 可能是一个很大的数字,因此需要设置数值上限来避免溢出。设置数值上限可以用取模的方式,即用 h % modulus 来代替原本的哈希值。
理论上,modules 应该取一个很大数,但具体应该取多大的数呢? 详见这篇文章,对于这个问题来说$ 2^{31} $就足够了。
算法
- 计算子字符串
haystack.substring(0, L)和needle.substring(0, L)的哈希值。 - 从起始位置开始遍历:从第一个字符遍历到第 N - L 个字符。
- 根据前一个哈希值计算滚动哈希。
- 如果子字符串哈希值与 needle 字符串哈希值相等,返回滑动窗口起始位置。
- 返回 -1,这时候 haystack 字符串中不存在 needle 字符串。
实现
class Solution {
// function to convert character to integer
public int charToInt(int idx, String s) {
return (int)s.charAt(idx) - (int)'a';
}
public int strStr(String haystack, String needle) {
int L = needle.length(), n = haystack.length();
if (L > n) return -1;
// base value for the rolling hash function
int a = 26;
// modulus value for the rolling hash function to avoid overflow
long modulus = (long)Math.pow(2, 31);
// compute the hash of strings haystack[:L], needle[:L]
long h = 0, ref_h = 0;
for (int i = 0; i < L; ++i) {
h = (h * a + charToInt(i, haystack)) % modulus;
ref_h = (ref_h * a + charToInt(i, needle)) % modulus;
}
if (h == ref_h) return 0;
// const value to be used often : a**L % modulus
long aL = 1;
for (int i = 1; i <= L; ++i) aL = (aL * a) % modulus;
for (int start = 1; start < n - L + 1; ++start) {
// compute rolling hash in O(1) time
h = (h * a - charToInt(start - 1, haystack) * aL
+ charToInt(start + L - 1, haystack)) % modulus;
if (h == ref_h) return start;
}
return -1;
}
}
复杂度分析
- 时间复杂度:O(N),计算 needle 字符串的哈希值需要 O(L)O(L) 时间,之后需要执行 (N - L)(N−L) 次循环,每次循环的计算复杂度为常数。
- 空间复杂度:O(1)。
方法四:Sunday算法
一、Sunday 匹配机制
匹配机制非常容易理解:
- 目标字符串
String - 模式串
Pattern - 当前查询索引
idx(初始为 0) - 待匹配字符串
str_cut:String [ idx : idx + len(Pattern) ]
每次匹配都会从 目标字符串中 提取 待匹配字符串与 模式串 进行匹配:
- 若匹配,则返回当前
idx - 不匹配,则查看 待匹配字符串 的后一位字符
c:- 若
c存在于Pattern中,则idx = idx + 偏移表[c] - 否则,
idx = idx + len(pattern)
- 若
Repeat Loop 直到 idx + len(pattern) > len(String)
二、偏移表
偏移表的作用是存储每一个在 模式串 中出现的字符,在 模式串 中出现的最右位置到尾部的距离 +1,例如 aab:
- a 的偏移位就是
len(pattern)-1 = 2 - b 的偏移位就是
len(pattern)-2 = 1 - 其他的均为
len(pattern)+1 = 4
综合一下:
三、举例
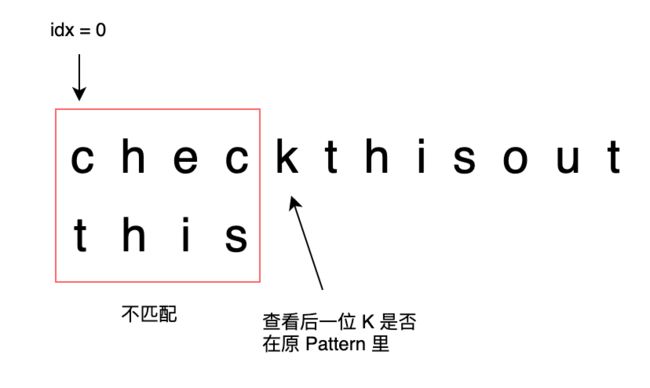
String: checkthisout
Pattern: this
Step 1:
- idx = 0
- 待匹配字符串为:
chec - 因为
chec != this - 所以查看
chec的下一个字符k k不在 Pattern 里- 所以查看 偏移表,
idx = idx + 5
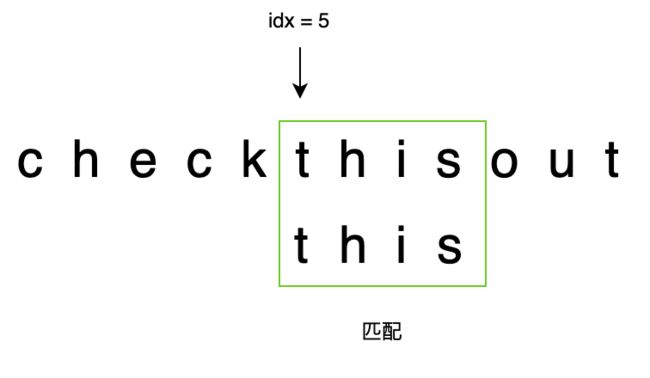
Step 2:
- idx = 5
- 待匹配字符串为:
this - 因为
this == this - 匹配,所以返回 5
四、算法分析
最坏情况:O(nm)
平均情况:O(n)
五、代码
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
# Func: 计算偏移表
def calShiftMat(st):
dic = {}
for i in range(len(st)-1,-1,-1):
if not dic.get(st[i]):
dic[st[i]] = len(st)-i
dic["ot"] = len(st)+1
return dic
# 其他情况判断
if len(needle) > len(haystack):return -1
if needle=="": return 0
# 偏移表预处理
dic = calShiftMat(needle)
idx = 0
while idx+len(needle) <= len(haystack):
# 待匹配字符串
str_cut = haystack[idx:idx+len(needle)]
# 判断是否匹配
if str_cut==needle:
return idx
else:
# 边界处理
if idx+len(needle) >= len(haystack):
return -1
# 不匹配情况下,根据下一个字符的偏移,移动idx
cur_c = haystack[idx+len(needle)]
if dic.get(cur_c):
idx += dic[cur_c]
else:
idx += dic["ot"]
return -1 if idx+len(needle) >= len(haystack) else idx
方法五:KMP算法
KMP 算法(Knuth-Morris-Pratt 算法)是一个著名的字符串匹配算法,效率很高,但是确实有点复杂。
很多读者抱怨 KMP 算法无法理解,这很正常,想到大学教材上关于 KMP 算法的讲解,也不知道有多少未来的 Knuth、Morris、Pratt 被提前劝退了。有一些优秀的同学通过手推 KMP 算法的过程来辅助理解该算法,这是一种办法,不过本文要从逻辑层面帮助读者理解算法的原理。十行代码之间,KMP 灰飞烟灭。
先在开头约定,本文用 pat 表示模式串,长度为 M,txt 表示文本串,长度为 N。KMP 算法是在 txt 中查找子串 pat,如果存在,返回这个子串的起始索引,否则返回 -1。
为什么我认为 KMP 算法就是个动态规划问题呢,等会再解释。对于动态规划,之前多次强调了要明确 dp 数组的含义,而且同一个问题可能有不止一种定义 dp 数组含义的方法,不同的定义会有不同的解法。
读者见过的 KMP 算法应该是,一波诡异的操作处理 pat 后形成一个一维的数组 next,然后根据这个数组经过又一波复杂操作去匹配 txt。时间复杂度 O(N),空间复杂度 O(M)。其实它这个 next 数组就相当于 dp 数组,其中元素的含义跟 pat 的前缀和后缀有关,判定规则比较复杂,不好理解。本文则用一个二维的 dp 数组(但空间复杂度还是 O(M)),重新定义其中元素的含义,使得代码长度大大减少,可解释性大大提高。
PS:本文的代码参考《算法4》,原代码使用的数组名称是 dfa(确定有限状态机),我对书中代码进行了一点修改,并沿用 dp 数组的名称。
本文会用到动态规划算法的设计技巧(归纳思想),所以希望读者看过这篇文章「动态规划设计之最长递增子序列」,很容易理解的。
一、KMP 算法概述
首先还是简单介绍一下 KMP 算法和暴力匹配算法的不同在哪里,难点在哪里,和动态规划有啥关系。
暴力的字符串匹配算法很容易写,看一下它的运行逻辑:
// 暴力匹配(伪码)
int search(String pat, String txt) {
int M = pat.length;
int N = txt.length;
for (int i = 0; i < N - M; i++) {
int j;
for (j = 0; j < M; j++) {
if (pat[j] != txt[i+j])
break;
}
// pat 全都匹配了
if (j == M) return i;
}
// txt 中不存在 pat 子串
return -1;
}
对于暴力算法,如果出现不匹配字符,同时回退 txt 和 pat 的指针,嵌套 for 循环,时间复杂度 O(MN),空间复杂度O(1)。最主要的问题是,如果字符串中重复的字符比较多,该算法就显得很蠢。
比如 txt = “aaacaaab” pat = “aaab”:
![]()
很明显,pat 中根本没有字符 c,根本没必要回退指针 i,暴力解法明显多做了很多不必要的操作。
KMP 算法的不同之处在于,它会花费空间来记录一些信息,在上述情况中就会显得很聪明:
![]()
再比如类似的 txt = “aaaaaaab” pat = “aaab”,暴力解法还会和上面那个例子一样蠢蠢地回退指针 i,而 KMP 算法又会耍聪明:
因为 KMP 算法知道字符 b 之前的字符 a 都是匹配的,所以每次只需要比较字符 b 是否被匹配就行了。
KMP 算法永不回退 txt 的指针 i,不走回头路(不会重复扫描 txt),而是借助 dp 数组中储存的信息把 pat 移到正确的位置继续匹配,时间复杂度只需 O(N),用空间换时间,所以我认为它是一种动态规划算法。
KMP 算法的难点在于,如何计算 dp 数组中的信息?如何根据这些信息正确地移动 pat 的指针?这个就需要确定有限状态自动机来辅助了,别怕这种高大上的文学词汇,其实和动态规划的 dp 数组如出一辙,等你学会了也可以拿这个词去吓唬别人。
还有一点需要明确的是:计算这个 dp 数组,只和 pat 串有关。意思是说,只要给我个 pat,我就能通过这个模式串计算出 dp 数组,然后你可以给我不同的 txt,我都不怕,利用这个 dp 数组我都能在 O(N) 时间完成字符串匹配。
具体来说,比如上文举的两个例子:
txt1 = "aaacaaab"
pat = "aaab"
txt2 = "aaaaaaab"
pat = "aaab"
我们的 txt 不同,但是 pat 是一样的,所以 KMP 算法使用的 dp 数组是同一个。
只不过对于 txt1 的下面这个即将出现的未匹配情况:
dp 数组指示 pat 这样移动:
PS:这个j 不要理解为索引,它的含义更准确地说应该是状态(state),所以它会出现这个奇怪的位置,后文会详述。
而对于 txt2 的下面这个即将出现的未匹配情况:
dp 数组指示 pat 这样移动:
明白了 dp 数组只和 pat 有关,那么我们这样设计 KMP 算法就会比较漂亮:
public class KMP {
private int[][] dp;
private String pat;
public KMP(String pat) {
this.pat = pat;
// 通过 pat 构建 dp 数组
// 需要 O(M) 时间
}
public int search(String txt) {
// 借助 dp 数组去匹配 txt
// 需要 O(N) 时间
}
}
这样,当我们需要用同一 pat 去匹配不同 txt 时,就不需要浪费时间构造 dp 数组了:
KMP kmp = new KMP("aaab");
int pos1 = kmp.search("aaacaaab"); //4
int pos2 = kmp.search("aaaaaaab"); //4
二、状态机概述
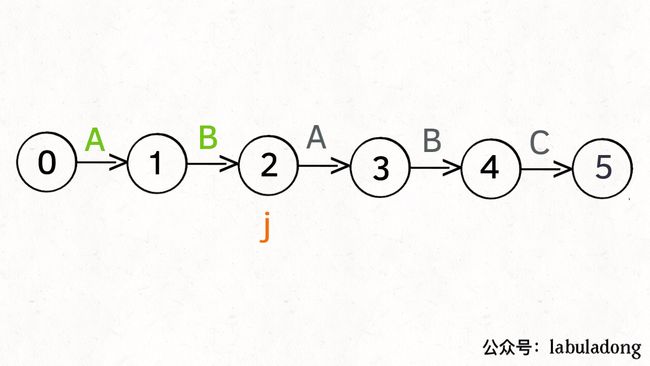
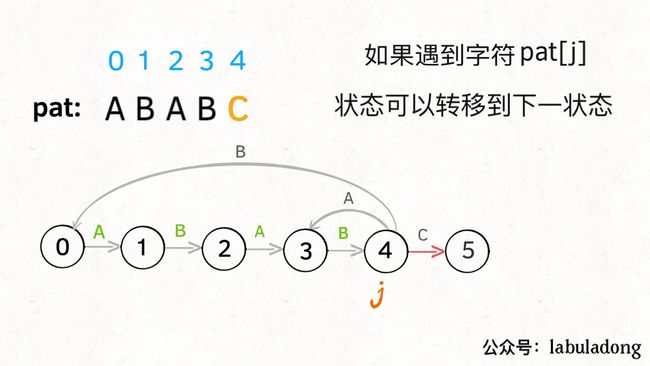
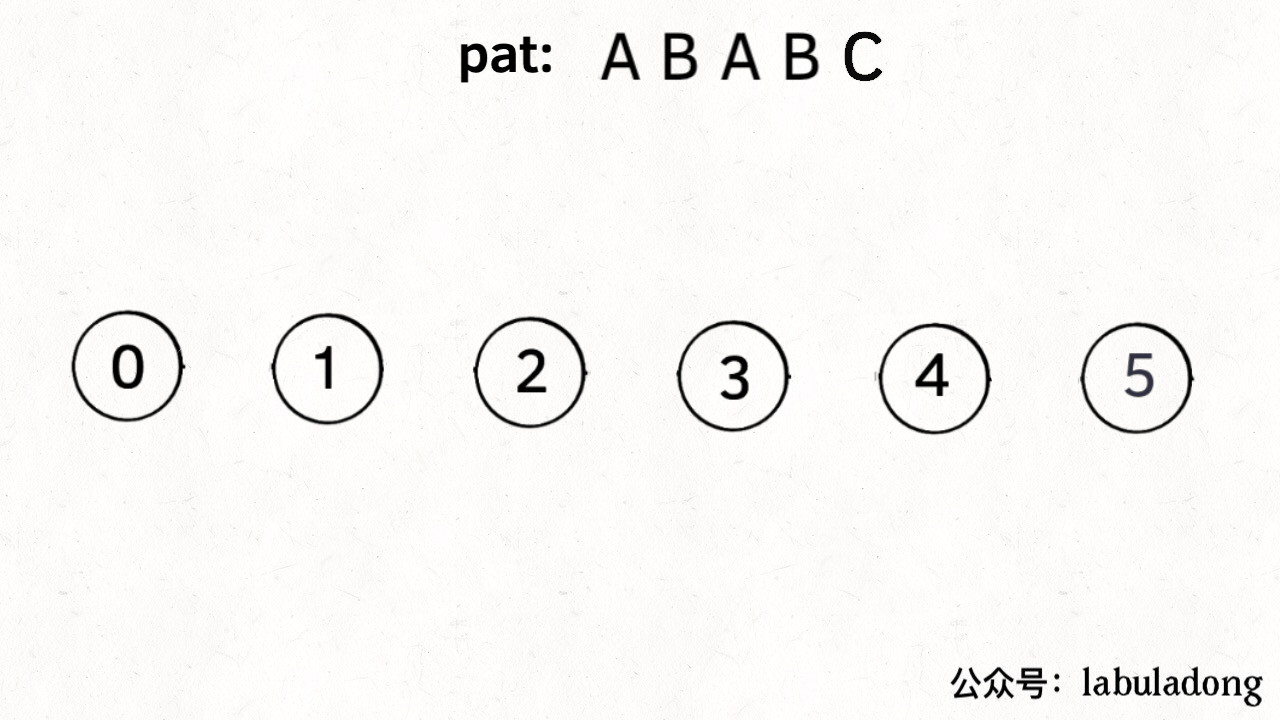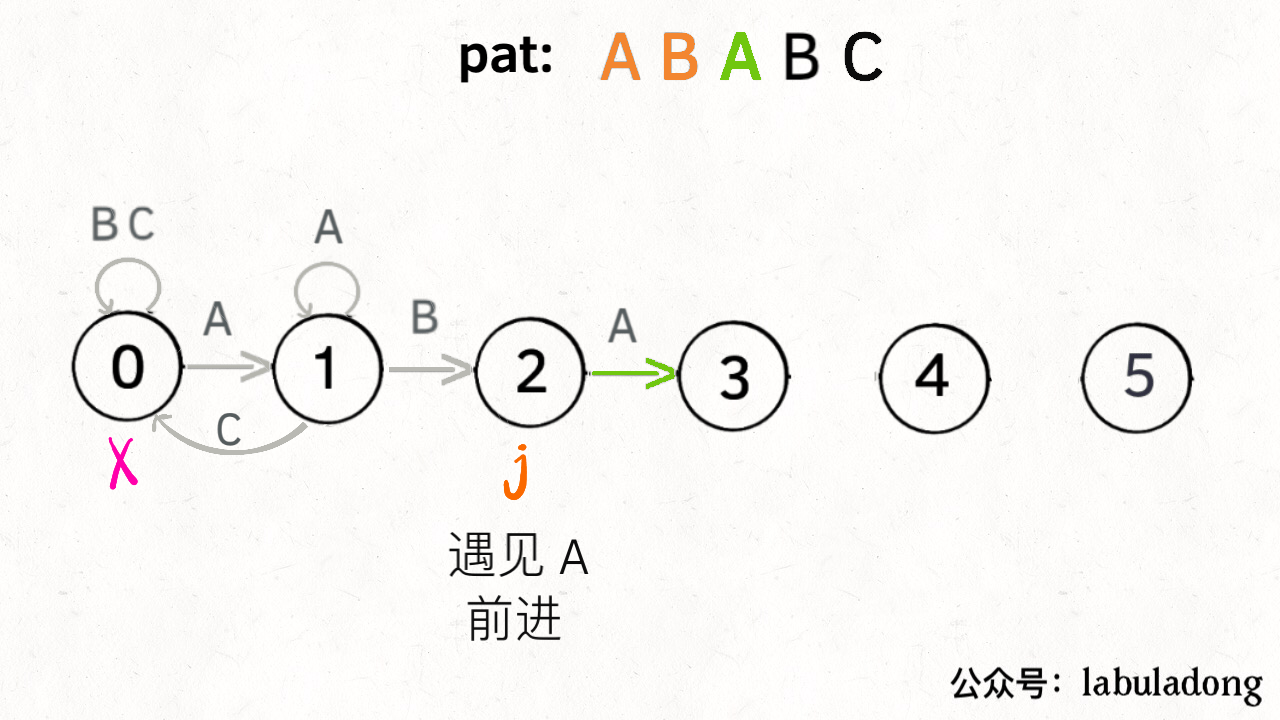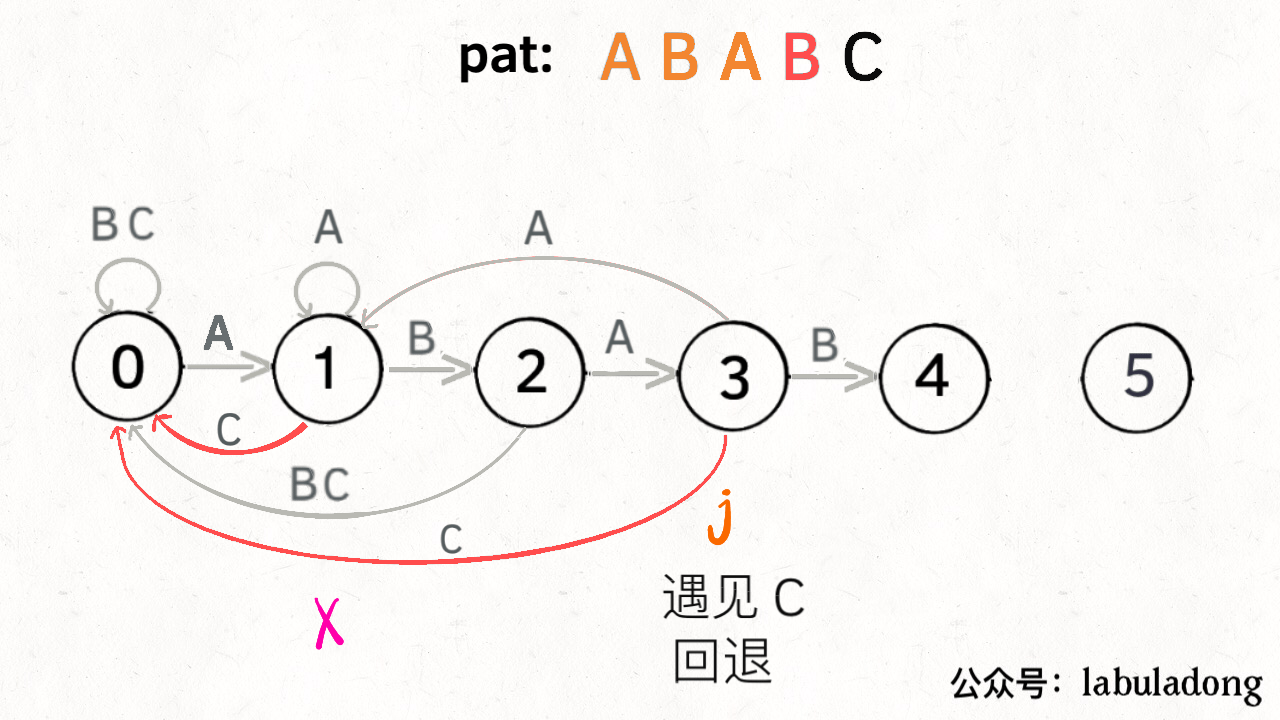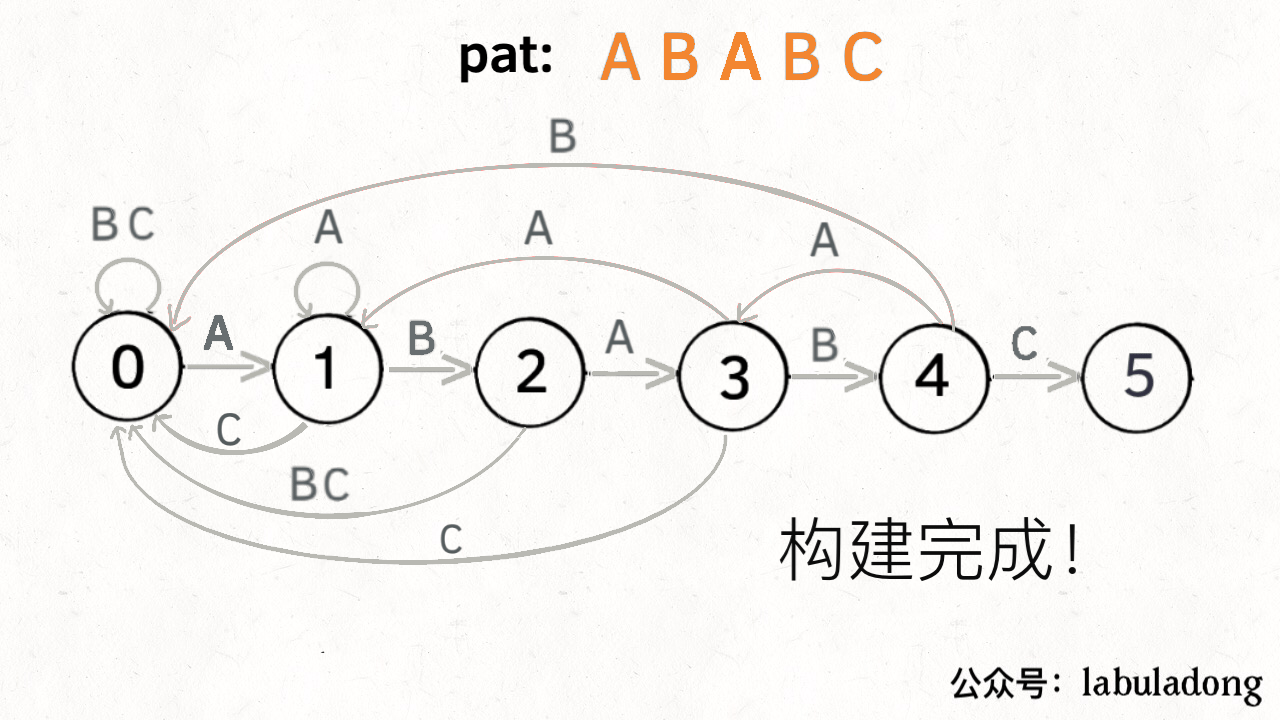
为什么说 KMP 算法和状态机有关呢?是这样的,我们可以认为 pat 的匹配就是状态的转移。比如当 pat = “ABABC”:
如上图,圆圈内的数字就是状态,状态 0 是起始状态,状态 5(pat.length)是终止状态。开始匹配时 pat 处于起始状态,一旦转移到终止状态,就说明在 txt 中找到了 pat。比如说当前处于状态 2,就说明字符 “AB” 被匹配:
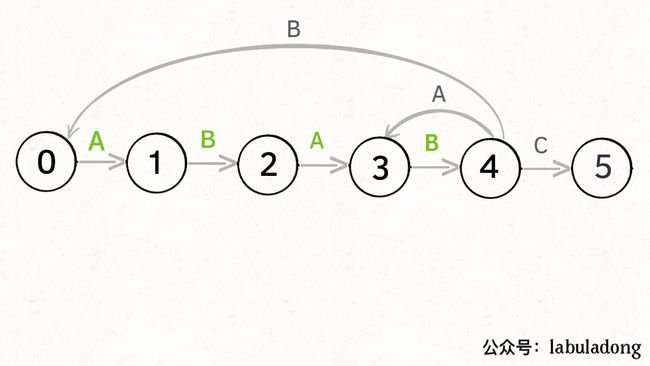
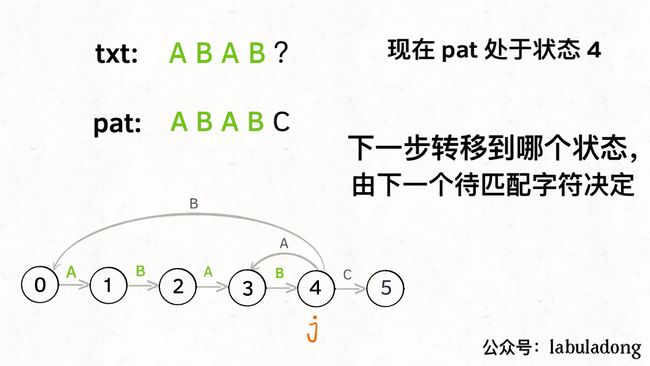
另外,处于不同状态时,pat 状态转移的行为也不同。比如说假设现在匹配到了状态 4,如果遇到字符 A 就应该转移到状态 3,遇到字符 C 就应该转移到状态 5,如果遇到字符 B 就应该转移到状态 0:
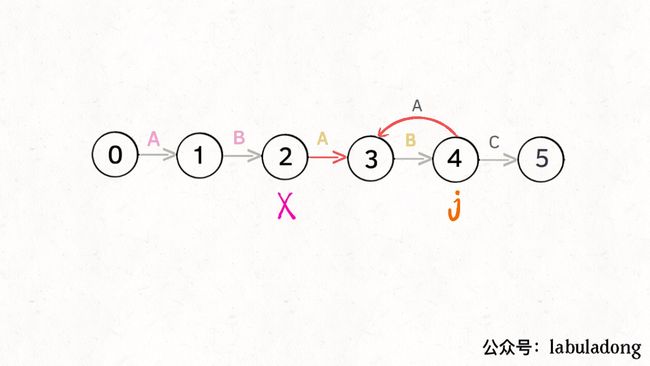
具体什么意思呢,我们来一个个举例看看。用变量 j 表示指向当前状态的指针,当前 pat 匹配到了状态 4:
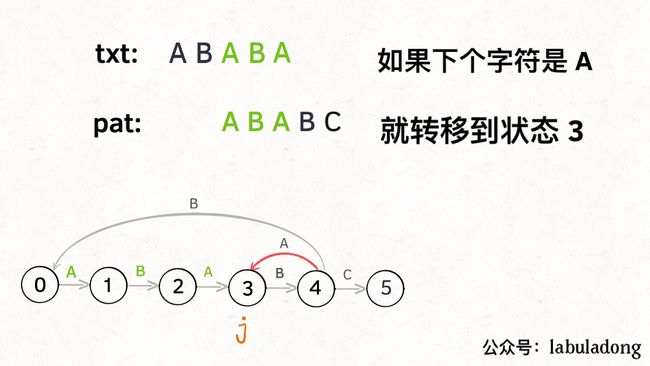
如果遇到了字符 “A”,根据箭头指示,转移到状态 3 是最聪明的:
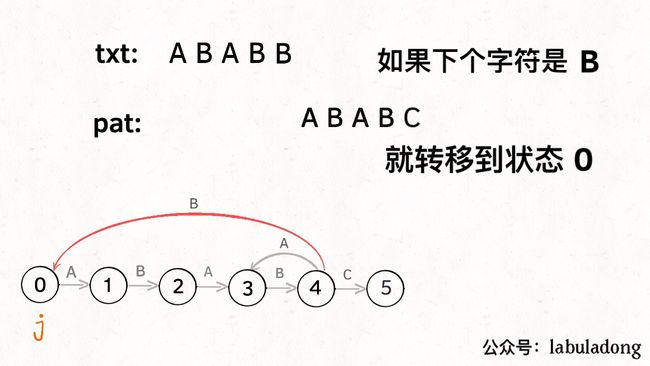
如果遇到了字符 “B”,根据箭头指示,只能转移到状态 0(一夜回到解放前):
如果遇到了字符 “C”,根据箭头指示,应该转移到终止状态 5,这也就意味着匹配完成:
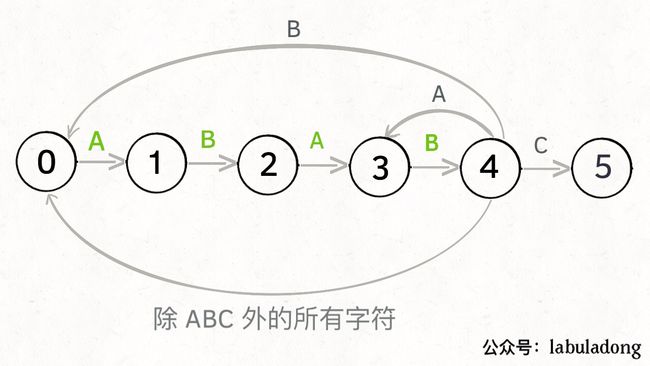
当然了,还可能遇到其他字符,比如 Z,但是显然应该转移到起始状态 0,因为 pat 中根本都没有字符 Z:
这里为了清晰起见,我们画状态图时就把其他字符转移到状态 0 的箭头省略,只画 pat 中出现的字符的状态转移:
KMP 算法最关键的步骤就是构造这个状态转移图。要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
下面看一下 KMP 算法根据这幅状态转移图匹配字符串 txt 的过程:
请记住这个 GIF 的匹配过程,这就是 KMP 算法的核心逻辑!
为了描述状态转移图,我们定义一个二维 dp 数组,它的含义如下:
dp[j][c] = next
0 <= j < M,代表当前的状态
0 <= c < 256,代表遇到的字符(ASCII 码)
0 <= next <= M,代表下一个状态
dp[4]['A'] = 3 表示:
当前是状态 4,如果遇到字符 A,
pat 应该转移到状态 3
dp[1]['B'] = 2 表示:
当前是状态 1,如果遇到字符 B,
pat 应该转移到状态 2
根据我们这个 dp 数组的定义和刚才状态转移的过程,我们可以先写出 KMP 算法的 search 函数代码:
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
// 如果达到终止态,返回匹配开头的索引
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
到这里,应该还是很好理解的吧,dp 数组就是我们刚才画的那幅状态转移图,如果不清楚的话回去看下 GIF 的算法演进过程。下面讲解:如何通过 pat 构建这个 dp 数组?
三、构建状态转移图
回想刚才说的:要确定状态转移的行为,必须明确两个变量,一个是当前的匹配状态,另一个是遇到的字符,而且我们已经根据这个逻辑确定了 dp 数组的含义,那么构造 dp 数组的框架就是这样:
for 0 <= j < M: # 状态
for 0 <= c < 256: # 字符
dp[j][c] = next
这个 next 状态应该怎么求呢?显然,如果遇到的字符 c 和 pat[j] 匹配的话,状态就应该向前推进一个,也就是说 next = j + 1,我们不妨称这种情况为状态推进:
如果字符 c 和 pat[j] 不匹配的话,状态就要回退(或者原地不动),我们不妨称这种情况为状态重启:
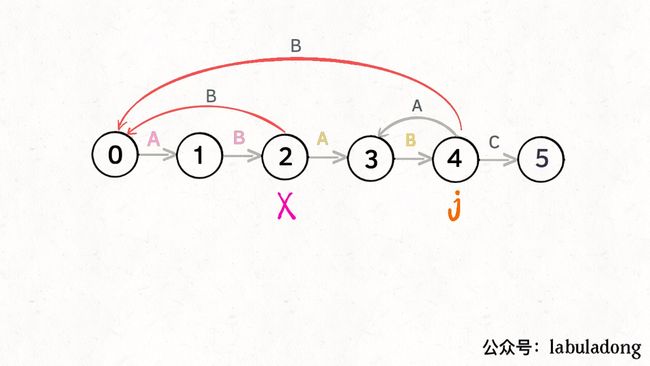
那么,如何得知在哪个状态重启呢?解答这个问题之前,我们再定义一个名字:影子状态(我编的名字),用变量 X 表示。所谓影子状态,就是和当前状态具有相同的前缀。比如下面这种情况:
当前状态 j = 4,其影子状态为 X = 2,它们都有相同的前缀 “AB”。因为状态 X 和状态 j 存在相同的前缀,所以当状态 j 准备进行状态重启的时候(遇到的字符 c 和 pat[j] 不匹配),可以通过 X 的状态转移图来获得最近的重启位置。
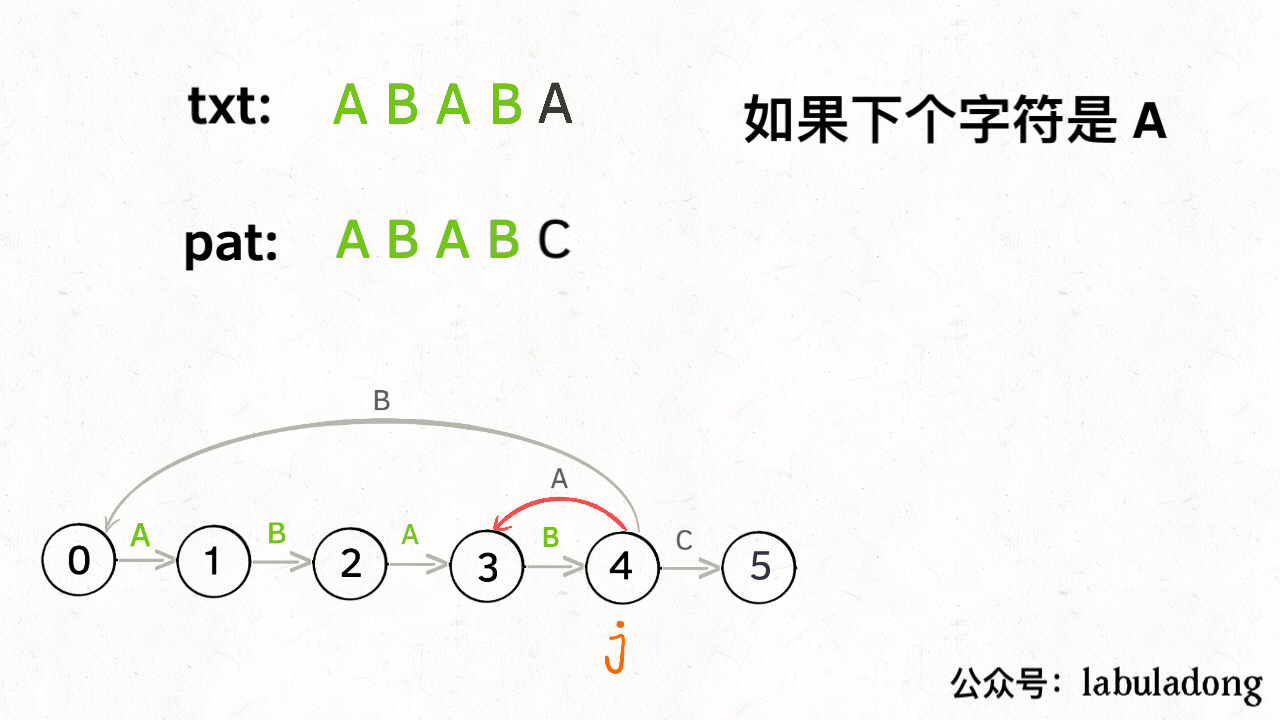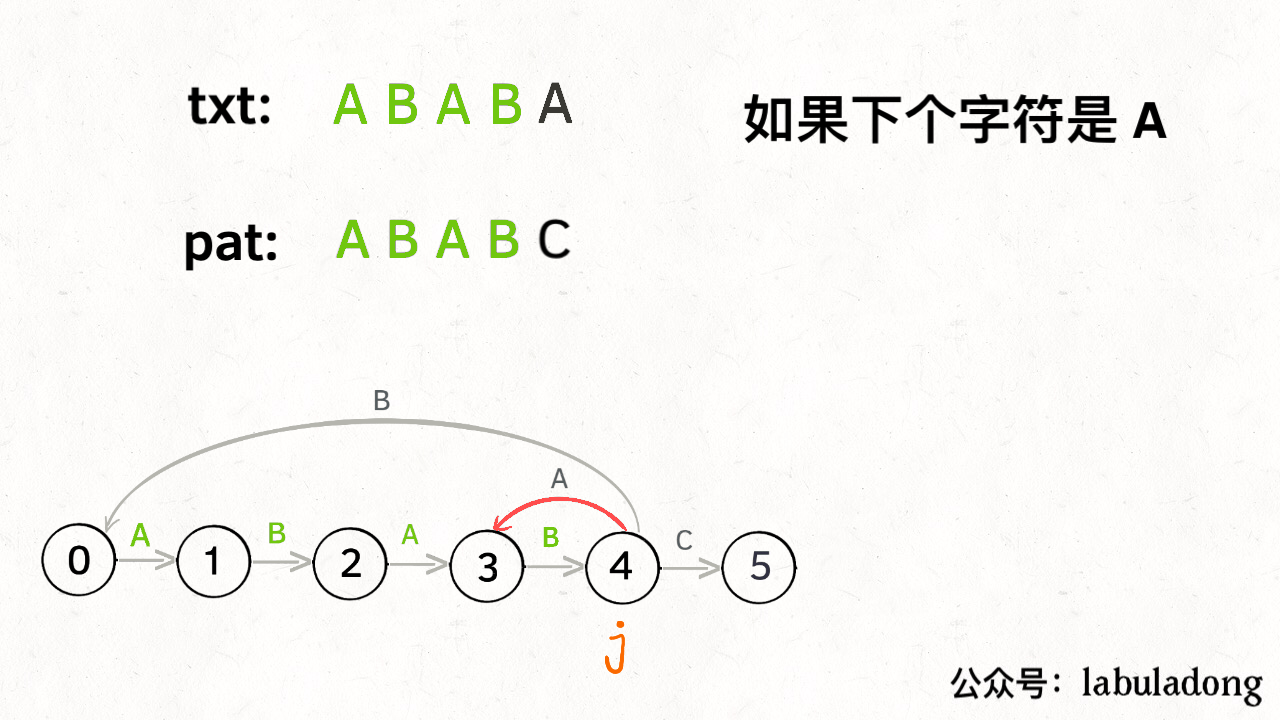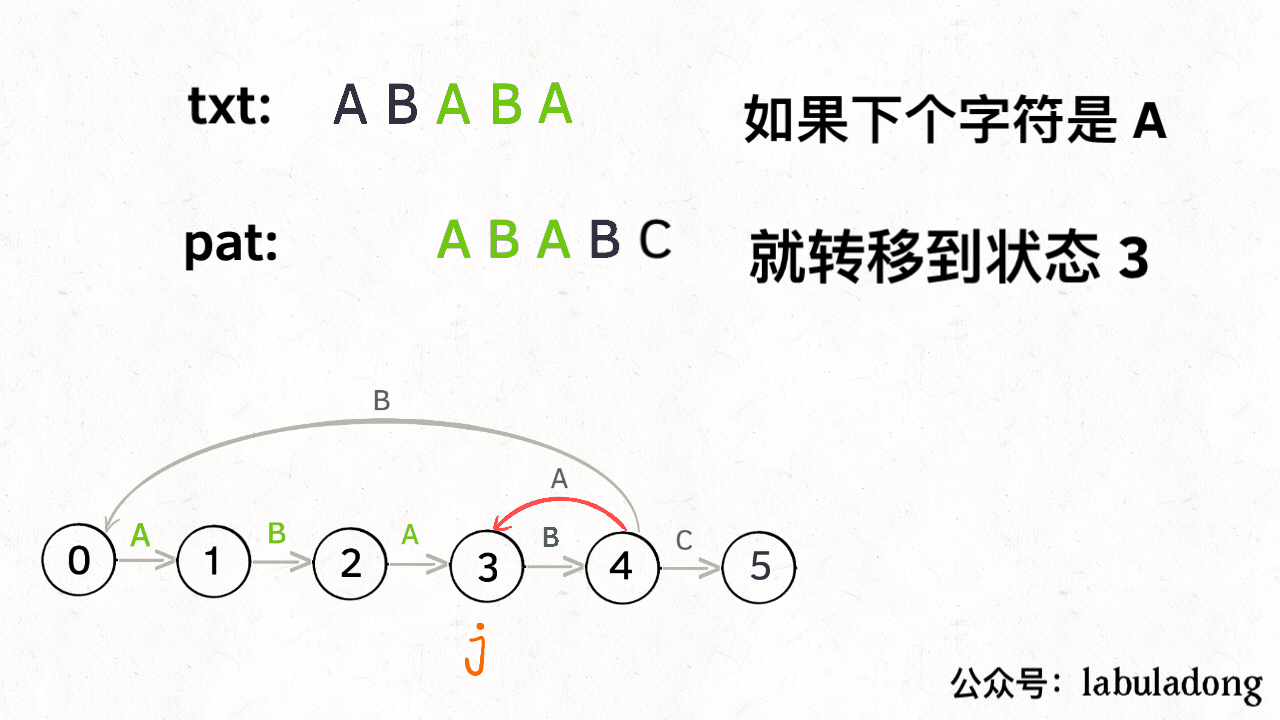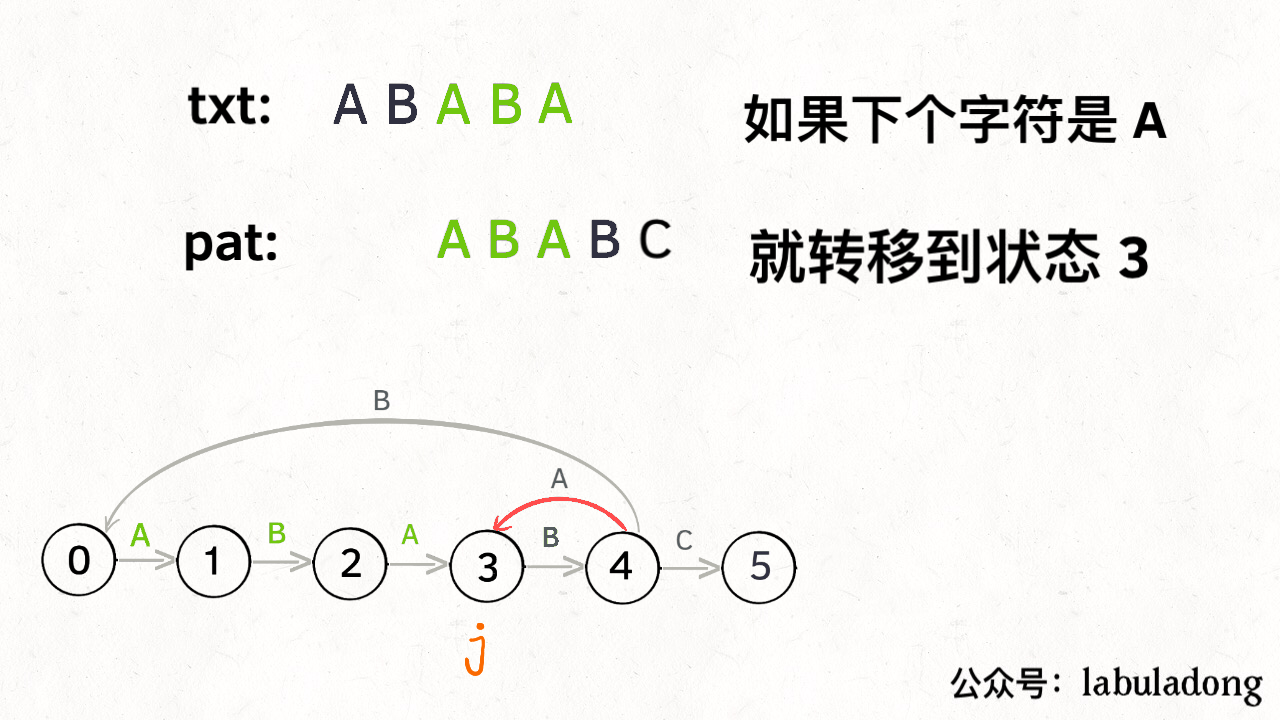
比如说刚才的情况,如果状态 j 遇到一个字符 “A”,应该转移到哪里呢?首先只有遇到 “C” 才能推进状态,遇到 “A” 显然只能进行状态重启。状态 j 会把这个字符委托给状态 X 处理,也就是 dp[j]['A'] = dp[X]['A']:
为什么这样可以呢?因为:既然 j 这边已经确定字符 “A” 无法推进状态,只能回退,而且 KMP 就是要尽可能少的回退,以免多余的计算。那么 j 就可以去问问和自己具有相同前缀的 X,如果 X 遇见 “A” 可以进行「状态推进」,那就转移过去,因为这样回退最少。
当然,如果遇到的字符是 “B”,状态 X 也不能进行「状态推进」,只能回退,j 只要跟着 X 指引的方向回退就行了:
你也许会问,这个 X 怎么知道遇到字符 “B” 要回退到状态 0 呢?因为 X 永远跟在 j 的身后,状态 X 如何转移,在之前就已经算出来了。动态规划算法不就是利用过去的结果解决现在的问题吗?
这样,我们就细化一下刚才的框架代码:
int X # 影子状态
for 0 <= j < M:
for 0 <= c < 256:
if c == pat[j]:
# 状态推进
dp[j][c] = j + 1
else:
# 状态重启
# 委托 X 计算重启位置
dp[j][c] = dp[X][c]
四、代码实现
如果之前的内容你都能理解,恭喜你,现在就剩下一个问题:影子状态 X 是如何得到的呢?下面先直接看完整代码吧。
public class KMP {
private int[][] dp;
private String pat;
public KMP(String pat) {
this.pat = pat;
int M = pat.length();
// dp[状态][字符] = 下个状态
dp = new int[M][256];
// base case
dp[0][pat.charAt(0)] = 1;
// 影子状态 X 初始为 0
int X = 0;
// 当前状态 j 从 1 开始
for (int j = 1; j < M; j++) {
for (int c = 0; c < 256; c++) {
if (pat.charAt(j) == c)
dp[j][c] = j + 1;
else
dp[j][c] = dp[X][c];
}
// 更新影子状态
X = dp[X][pat.charAt(j)];
}
}
public int search(String txt) {...}
}
先解释一下这一行代码:
// base case
dp[0][pat.charAt(0)] = 1;
这行代码是 base case,只有遇到 pat[0] 这个字符才能使状态从 0 转移到 1,遇到其它字符的话还是停留在状态 0(Java 默认初始化数组全为 0)。
影子状态 X 是先初始化为 0,然后随着 j 的前进而不断更新的。下面看看到底应该如何更新影子状态 X:
int X = 0;
for (int j = 1; j < M; j++) {
...
// 更新影子状态
// 当前是状态 X,遇到字符 pat[j],
// pat 应该转移到哪个状态?
X = dp[X][pat.charAt(j)];
}
更新 X 其实和 search 函数中更新状态 j 的过程是非常相似的:
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
...
}
其中的原理非常微妙,注意代码中 for 循环的变量初始值,可以这样理解:后者是在 txt 中匹配 pat,前者是在 pat 中匹配 pat[1..end],状态 X 总是落后状态 j 一个状态,与 j 具有最长的相同前缀。所以我把 X 比喻为影子状态,似乎也有一点贴切。
另外,构建 dp 数组是根据 base case dp[0][..] 向后推演。这就是我认为 KMP 算法就是一种动态规划算法的原因。
下面来看一下状态转移图的完整构造过程,你就能理解状态 X 作用之精妙了:
至此,KMP 算法的核心终于写完啦啦啦啦!看下 KMP 算法的完整代码吧:
public class KMP {
private int[][] dp;
private String pat;
public KMP(String pat) {
this.pat = pat;
int M = pat.length();
// dp[状态][字符] = 下个状态
dp = new int[M][256];
// base case
dp[0][pat.charAt(0)] = 1;
// 影子状态 X 初始为 0
int X = 0;
// 构建状态转移图(稍改的更紧凑了)
for (int j = 1; j < M; j++) {
for (int c = 0; c < 256; c++) {
dp[j][c] = dp[X][c];
dp[j][pat.charAt(j)] = j + 1;
// 更新影子状态
X = dp[X][pat.charAt(j)];
}
}
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 计算 pat 的下一个状态
j = dp[j][txt.charAt(i)];
// 到达终止态,返回结果
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
}
经过之前的详细举例讲解,你应该可以理解这段代码的含义了,当然你也可以把 KMP 算法写成一个函数。核心代码也就是两个函数中 for 循环的部分,数一下有超过十行吗?
五、最后总结
传统的 KMP 算法是使用一个一维数组 next 记录前缀信息,而本文是使用一个二维数组 dp 以状态转移的角度解决字符匹配问题,但是空间复杂度仍然是$ O(256M) = O(M)$。
在 pat 匹配 txt 的过程中,只要明确了「当前处在哪个状态」和「遇到的字符是什么」这两个问题,就可以确定应该转移到哪个状态(推进或回退)。
对于一个模式串 pat,其总共就有 M 个状态,对于 ASCII 字符,总共不会超过 256 种。所以我们就构造一个数组 dp[M][256] 来包含所有情况,并且明确 dp 数组的含义:
dp[j][c] = next 表示,当前是状态 j,遇到了字符 c,应该转移到状态 next。
明确了其含义,就可以很容易写出 search 函数的代码。
对于如何构建这个 dp 数组,需要一个辅助状态 X,它永远比当前状态 j 落后一个状态,拥有和 j 最长的相同前缀,我们给它起了个名字叫「影子状态」。
在构建当前状态 j 的转移方向时,只有字符 pat[j] 才能使状态推进(dp[j][pat[j]] = j+1);而对于其他字符只能进行状态回退,应该去请教影子状态 X 应该回退到哪里(dp[j][other] = dp[X][other],其中 other 是除了 pat[j] 之外所有字符)。
对于影子状态 X,我们把它初始化为 0,并且随着 j 的前进进行更新,更新的方式和 search 过程更新 j 的过程非常相似(X = dp[X][pat[j]])。
KMP 算法也就是动态规划那点事,而且都是按照一套框架来的,无非就是描述问题逻辑,明确 dp 数组含义,定义 base case 这点破事。希望这篇文章能让大家对动态规划有更深的理解。
。
在 pat 匹配 txt 的过程中,只要明确了「当前处在哪个状态」和「遇到的字符是什么」这两个问题,就可以确定应该转移到哪个状态(推进或回退)。
对于一个模式串 pat,其总共就有 M 个状态,对于 ASCII 字符,总共不会超过 256 种。所以我们就构造一个数组 dp[M][256] 来包含所有情况,并且明确 dp 数组的含义:
dp[j][c] = next 表示,当前是状态 j,遇到了字符 c,应该转移到状态 next。
明确了其含义,就可以很容易写出 search 函数的代码。
对于如何构建这个 dp 数组,需要一个辅助状态 X,它永远比当前状态 j 落后一个状态,拥有和 j 最长的相同前缀,我们给它起了个名字叫「影子状态」。
在构建当前状态 j 的转移方向时,只有字符 pat[j] 才能使状态推进(dp[j][pat[j]] = j+1);而对于其他字符只能进行状态回退,应该去请教影子状态 X 应该回退到哪里(dp[j][other] = dp[X][other],其中 other 是除了 pat[j] 之外所有字符)。
对于影子状态 X,我们把它初始化为 0,并且随着 j 的前进进行更新,更新的方式和 search 过程更新 j 的过程非常相似(X = dp[X][pat[j]])。
KMP 算法也就是动态规划那点事,而且都是按照一套框架来的,无非就是描述问题逻辑,明确 dp 数组含义,定义 base case 这点破事。希望这篇文章能让大家对动态规划有更深的理解。