C++解决最大子段和问题

给定由n个整数（可能为负整数）组成的序列a[1],a[2],a[3],…,a[n],最大子段和问题（sum of largest sub-segment problem）要求该序列如a[i]+a[i+1]+…+a[j]的最大值，当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为：Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-20,11,-4,13,-5,-2)时，最大子段和为20。
在本文中，将介绍两种方法（蛮力法、动态规划法）并分别分析两种方法的时间效率。

蛮力法

蛮力法解决本问题非常简单粗暴，直接用循环嵌套，比较所有子段和的大小，最后输出最大子段和。

代码如下：

#include
using namespace std;
int MaxSubsegmentSum1(int n,int array[])
{
	int Max=0;
	for(int i=0;i<n;i++)   //起始位置 
	{
		for(int j=i;j<n;j++)   //结束位置 
		{
			int sum=0;
			for(int k=i;k<=j;k++)   //求从i到j的子段和 
			{
				sum=sum+array[k];
			}
			if(sum>Max)
			{
				Max=sum;
			}
		}
	}
	return Max;
}

int main()
{
	int n;
	cout<<"请输入该序列有多少个数字：";
	cin>>n;
	int array[n];
	cout<<"请依次输入数字："<<endl; 
	for(int i=0;i<n;i++)
	{
		cin>>array[i];
	}
	int MaxSubSum1=MaxSubsegmentSum1(n,array);
	cout<< "最大子段和为：" <<MaxSubSum1;
}

动态规划法

动态规划法解决本问题则要巧妙很多，让我们先看看代码：

#include
using namespace std;
int MaxSubsegmentSum2(int n,int array[])
{
	int MAX=0,a=0;
	for(int i=0;i<n;i++)
	{
		if(a>0)
		{
			a=a+array[i];
		}else
		{
			a=array[i];
		}
		if(a>MAX)
		{
			MAX=a;
		}
	}
	return MAX;
}

int main()
{
	int n;
	cout<<"请输入该序列有多少个数字：";
	cin>>n;
	int array[n];
	cout<<"请依次输入数字："<<endl; 
	for(int i=0;i<n;i++)
	{
		cin>>array[i];
	}
	int MaxSubSum2=MaxSubsegmentSum2(n,array);
	cout<< "最大子段和为：" <<MaxSubSum2;
}

我们可以看到，在循环中做了判断当a大于0的时候a才会加array【i】，而当a小于或等于0的时候a就等于array【i】，这可以保证子段和从正整数开始加，而最后如果a大于max的话，将a的值赋给max，得到最大子段和。（为什么要设置a的初始值为0呢，这可以保证当所有数都为负数时，最大子段和为0）

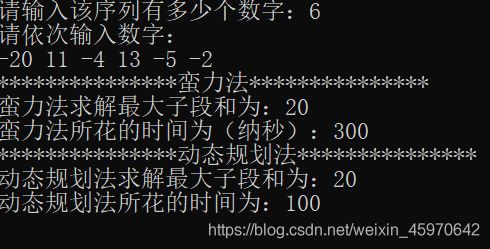
时间性能对比

下面编写了一个代码来比较两种算法的时间性能对比，来看看动态规划法是否在解决本问题中有着更高的效率。

代码如下：

#include 
#include 
#include 
#include
using namespace std;
int MaxSubsegmentSum1(int n,int array[])
{
	int Max=0;
	for(int i=0;i<n;i++)
	{
		for(int j=i;j<n;j++)
		{
			int temp=0;
			for(int k=i;k<=j;k++)
			{
				temp=temp+array[k];
			}
			if(temp>Max)
			{
				Max=temp;
			}
		}
	}
	return Max;
}
int MaxSubsegmentSum2(int n,int array[])
{
	int MAX=0,a=0;
	for(int i=0;i<n;i++)
	{
		if(a>0)
		{
			a=a+array[i];
		}else
		{
			a=array[i];
		}
		if(a>MAX)
		{
			MAX=a;
		}
	}
	return MAX;
}

int main()
{
	int n;
	LARGE_INTEGER nFreq1,nFreq2;
    LARGE_INTEGER nBeginTime1,nBeginTime2;
    LARGE_INTEGER nEndTime1,nEndTime2;
    double time1,time2;
	cout<<"请输入该序列有多少个数字：";
	cin>>n;
	int array[n];
	cout<<"请依次输入数字："<<endl; 
	for(int i=0;i<n;i++)
	{
		cin>>array[i];
	}
	cout<<"***************蛮力法***************"<<endl;
	int MaxSubSum1=MaxSubsegmentSum1(n,array);
	cout<<"蛮力法求解最大子段和为："<<MaxSubSum1<<endl;
	QueryPerformanceFrequency(&nFreq1);
    QueryPerformanceCounter(&nBeginTime1); 
   
    MaxSubsegmentSum1(n,array);
    QueryPerformanceCounter(&nEndTime1);
    time1=(double)(nEndTime1.QuadPart-nBeginTime1.QuadPart)*1000000000/(double)(nFreq1.QuadPart);
    co![在这里插入图片描述](https://img-blog.csdnimg.cn/20200601112048417.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTk3MDY0Mg==,size_16,color_FFFFFF,t_70)ut<<"蛮力法所花的时间为（纳秒）："<<time1<<endl; //单位是纳秒. 
    
    cout<<"***************动态规划法***************"<<endl;
	int MaxSubSum2=MaxSubsegmentSum2(n,array);
	cout<<"动态规划法求解最大子段和为："<<MaxSubSum2<<endl;
	QueryPerformanceFrequency(&nFreq2);
    QueryPerformanceCounter(&nBeginTime2); 
   
    MaxSubsegmentSum2(n,array);
    QueryPerformanceCounter(&nEndTime2);
    time2=(double)(nEndTime2.QuadPart-nBeginTime2.QuadPart)*1000000000/(double)(nFreq2.QuadPart);
    cout<<"动态规划法所花的时间为："<<time2<<endl; //单位是纳秒.
}

运行结果如下：

可见，比起用蛮力法简单粗暴解决问题，动态规划法确实有着更高的时间效率。