LeetCode 力扣 79. 单词搜索

题目描述（中等难度）

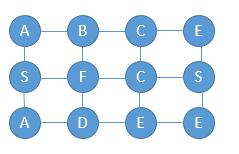
意思就是从某个字符出发，然后它可以向左向右向上向下移动，走过的路径构成一个字符串，判断是否能走出给定字符串的 word ，还有一个条件就是走过的字符不能够走第二次。

比如 SEE，从第二行最后一列的 S 出发，向下移动，再向左移动，就走出了 SEE。

ABCB，从第一行第一列的 A 出发，向右移动，再向右移动，到达 C 以后，不能向左移动回到 B ，并且也没有其他的路径走出 ABCB 所以返回 false。

解法一 DFS

我们可以把矩阵看做一个图，然后利用图的深度优先遍历 DFS 的思想就可以了。

我们需要做的就是，在深度优先遍历过程中，判断当前遍历元素是否对应 word 元素，如果不匹配就结束当前的遍历，返回上一次的元素，尝试其他路径。当然，和普通的 dfs 一样，我们需要一个 visited 数组标记元素是否访问过。

public boolean exist(char[][] board, String word) {
    int rows = board.length;
    if (rows == 0) {
        return false;
    }
    int cols = board[0].length;
    boolean[][] visited = new boolean[rows][cols];
    //从不同位置开始
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            //从当前位置开始符合就返回 true
            if (existRecursive(board, i, j, word, 0, visited)) {
                return true;
            }
        }
    }
    return false;
}

private boolean existRecursive(char[][] board, int row, int col, String word, int index, boolean[][] visited) {
    //判断是否越界
    if (row < 0 || row >= board.length || col < 0 || col >= board[0].length) {
        return false;
    }
    //当前元素访问过或者和当前 word 不匹配返回 false
    if (visited[row][col] || board[row][col] != word.charAt(index)) {
        return false;
    }
    //已经匹配到了最后一个字母，返回 true
    if (index == word.length() - 1) {
        return true;
    }
    //将当前位置标记位已访问
    visited[row][col] = true;
    //对四个位置分别进行尝试
    boolean up = existRecursive(board, row - 1, col, word, index + 1, visited);
    if (up) {
        return true;
    }
    boolean down = existRecursive(board, row + 1, col, word, index + 1, visited);
    if (down) {
        return true;
    }
    boolean left = existRecursive(board, row, col - 1, word, index + 1, visited);
    if (left) {
        return true;
    }
    boolean right = existRecursive(board, row, col + 1, word, index + 1, visited);
    if (right) {
        return true;
    }
    //当前位置没有选进来，恢复标记为 false
    visited[row][col] = false;
    return false; 
}

我们可以优化一下空间复杂度，我们之前是用了一个等大的二维数组来标记是否访问过。其实我们完全可以用之前的 board，我们把当前访问的元素置为 “$” ，也就是一个在 board 中不会出现的字符。然后当上下左右全部尝试完之后，我们再把当前元素还原就可以了。

public boolean exist(char[][] board, String word) {
    int rows = board.length;
    if (rows == 0) {
        return false;
    }
    int cols = board[0].length;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            if (existRecursive(board, i, j, word, 0)) {
                return true;
            }
        }
    }
    return false;
}

private boolean existRecursive(char[][] board, int row, int col, String word, int index) {
    if (row < 0 || row >= board.length || col < 0 || col >= board[0].length) {
        return false;
    }
    if (board[row][col] != word.charAt(index)) {
        return false;
    }
    if (index == word.length() - 1) {
        return true;
    }
    /*********************改变的地方****************************************/
    char temp = board[row][col];
    board[row][col] = '$';
    /*********************************************************************/
    boolean up = existRecursive(board, row - 1, col, word, index + 1);
    if (up) {
        return true;
    }
    boolean down = existRecursive(board, row + 1, col, word, index + 1);
    if (down) {
        return true;
    }
    boolean left = existRecursive(board, row, col - 1, word, index + 1);
    if (left) {
        return true;
    }
    boolean right = existRecursive(board, row, col + 1, word, index + 1);
    if (right) {
        return true;
    }
    /*********************改变的地方****************************************/
    board[row][col] = temp;
    /*********************************************************************/
    return false;
}

在这里，看到另外一种标记和还原的方法。异或。

/*********************之前的做法****************************************/
char temp = board[row][col];
board[row][col] = '$';
/*********************************************************************/

/*********************利用异或****************************************/
board[row][col] ^= 128;
/*********************************************************************/

//还原
/********************之前的做法****************************************/
board[row][col] = temp;
/*********************************************************************/

/*********************利用异或****************************************/
board[row][col] ^= 128;
/*********************************************************************/

至于原理，因为 ASCII 码值的范围是 0 - 127，二进制的话就是 0000 0000 - 0111 1111，我们把它和 128 做异或，也就是和 1000 0000 。这样，如果想还原原来的数字只需要再异或 128 就可以了。

其实原理是一样的，都是把之前的数字变成当前 board 不存在的字符，然后再变回来。只不过这里考虑它的二进制编码，在保留原有信息的基础上做改变，不再需要 temp 变量。

总

关键是对题目的理解，抽象到 DFS，题目就迎刃而解了。异或的应用很强。

更多详细通俗题解详见 leetcode.wang 。