算法设计与分析基础 第三章谜题
习题3.1
6.四格拼板 四格拼板是由4个1*1的正方形组成。下面是5种类型的四格拼板:
分别利用以下四格拼板,看看是否有可能在不重叠的情况下完全覆盖一个8*8的棋盘。
a. 直线拼板 可以,长和宽能被8整除
b. 方形拼板 可以,边长能被8整除
c. L形拼板 可以,两个拼板组成2*4拼板,长和宽能被8整除
d. T形拼板 可以,用四个拼板组成4*4拼板,边长能被8整除
e. Z形拼板 不可能,用Z形拼板无法拼出一个完整的直角
7.一摞假币 有n摞硬币,每摞包含n个硬币,硬币外观完全相同。其中一摞硬币全是假币,而其他摞全是真币。每个真币重10克,每个假币重11克。你有一个称重盘,可以对任意数量硬币精确称重。
a. 设计一个蛮力算法识别那摞假币,并且确定该算法最坏情况的效率类型
解答:每摞硬币都取出一枚硬币,依次称重,直到称出11克的硬币,则该硬币以及同一摞为假币。最坏称重n次,效率类型为θ(n)。
b. 要识别出那摞假币,至少需要称重多少次?
解答:称重一次即可。给每摞硬币从1到n标号,每一摞取出一些硬币,取出数量即为标号,对这堆硬币称重为x克,若全为真币重量为y克,x-y即为假币对应标号。
14.交叉放置的碟子 我们有数量为2n的一排碟子,n黑n白交替放置:黑、白、黑、白……现在要把黑碟子都放在右边,白碟子都放在左边,但只允许通过互换相邻碟子的位置来实现。为该谜题写个算法,并确定该算法需要执行的换位次数。
解答:用1表示黑碟子,0表示白碟子,那么目前的顺序是:1010...1010。结果要求1都放在右边,0都放在左边。这个题目看起来与冒泡排序相似。假设目前有6个碟子:101010。使用冒泡排序,第一次迭代,碟子序列变为:010101,交换3次。在进行第二次迭代之前,观察一下。现在,不仅第一个碟子就位,最后一个也是了,因此第二次迭代只需要对第2到第5个进行排序,巧合的是,碟子[2->5]仍然是10交替出现,不过比上一次少了两个,可以得到结论:对于2n个碟子,可以使用n次迭代完成,交换的次数分别是:n+(n-1)+...+2+1,即n(n+1)/2。
习题3.2
3.仪器测试 某公司总部大楼有n层,为了测出哪层楼最高,可以用一种仪器从天花板向地板自由落体(当然仪器并不会摔坏)。公司有两个一模一样的仪器来进行测试。如果这两个仪器的其中一个受损,而且无法修复,实验不得不用剩下的仪器独立完成。请设计一个具有最佳效率类型的算法来帮该公司解决这个问题。
解答:此题翻译有误,原文是:A firm wants to determine the highest floor of its n-story headquarters from which a gadget can fall without breaking. The firm has two identical gadgets to experiment with. If one of them gets broken, it can not be repaired, and the experiment will have to be completed with the remaining gadget. Design an algorithm in the best efficiency class you can to solve this problem.
题目与两个鸡蛋下落问题类似,第一次到k楼去测,如果摔坏了,只有从1,2,...k-1一个个去测,如果没有坏,第二次到k+(k-1)楼去测,如果摔坏了,只有从k+1,k+2,...k+(k-2)一个个去测,如果没有坏,第三次到k+(k-1)+(k-2)楼去测,如果摔坏了,只有从k+(k-1)+1,k+(k-1)+2,...k+(k-1)+(k-3)一个个去测,如果没有坏,。。。,最后到k+(k-1)+(k-2)+...+1楼去测,则有k+(k-1)+(k-2)+...+1= k(k+1)/2>=n,可得到k,即平均测试次数为k次,效率类型为O(![]() )
)
10.填字游戏 “填字”是在美国流行的一种游戏,它要求游戏者从一张填满字母的正方形表中,找出包含在一个给定集合中的所有词。这些词可以竖着读,横着读,或者沿45°对角线斜着读,但这些词必须是由表格中邻接的连续单元格构成。遇到表格的边界时可以环绕,但方向不得改变,也不能折来折去。表格中的同一单元格可以出现在不同的词中,但在任一词中,同一单元格不得出现一次以上。为该游戏设计一个计算机程序。
解答:遍历正方形表的所有位置,以每个位置为起始,分别向八个方向出发,寻找是否有单词出现。注意在边界的位置只需往5个方向搜索,在顶角的位置只需往三个方向搜索。
11.海战游戏 基于蛮力模式匹配,在计算机上编程实现“海战”游戏。游戏的规则如下:游戏中有两个对手(在这里,分别是玩家和计算机),游戏在两块完全相同的棋盘(10*10的方格)上进行的,两个对手分别在各自的棋盘上放置他们的舰艇,当然对手是看不见的。每一个对手都有5艘舰艇:一艘驱逐舰(2格)、一艘潜艇(3格)、一艘巡洋舰(3格)、一艘战列舰(4格)和一艘航空母舰(5格)。每艘舰艇都在棋盘上占据一定数量的格子。每艘舰艇既可以竖着放,也可以横着放,但任意两艘舰艇不能互相接触。游戏的玩法是双方轮流“轰炸”对方的舰艇。每次轰炸的结果是击中还是未击中都会显示出来。如果击中的话,该玩家就可以继续攻击,直到击不中为止。游戏的目标是赶在对手之前把他所有的舰艇都击沉。要击沉一艘潜艇,该舰艇的所有格子都必须命中。
#include
#include //rand()%(x) 0~x-1 int
#include //停顿:Sleep();
#include //清屏:system("cls");
#include //_getch(); char
#include
#include //未知 :□; 打中 :◎; 未打中:○ 船:★;
using namespace std;
int rest[3][6], r1, r2; //rest[1]:玩家的海域; rest[2]:电脑的海域 r1:玩家还剩船数; r2:电脑还剩船数
int b1[12][12], b2[12][12]; //0:空海; 1:船只; 2:打中; 3:边界 4:未打中 5:沉船
int c1[12][12], c2[12][12]; //c1:玩家海域的颜色 c2:电脑海域颜色
int fx[8][2] = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 }, { 1, 1 }, { -1, -1 }, { 1, -1 }, { -1, 1 } };
int now[2][2]; //now[左/右][x/y] 光标
string a1[12][12], a2[12][12];
int fd[500][2], head = 0, tail = 0;
void color(int a)//颜色函数
{
SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), a);
}
void gotoxy(int x, int y)//位置函数(整个界面)(行为x 列为y)
{
COORD pos;
pos.X = 2 * (y);
pos.Y = x;
SetConsoleCursorPosition(GetStdHandle(STD_OUTPUT_HANDLE), pos);
}
void gotoxy1(int x, int y)//位置函数(左边棋盘)(行为x 列为y)
{
COORD pos;
pos.X = 2 * (y + 5);
pos.Y = x + 1;
SetConsoleCursorPosition(GetStdHandle(STD_OUTPUT_HANDLE), pos);
}
void gotoxy2(int x, int y)//位置函数(右边棋盘)(行为x 列为y)
{
COORD pos;
pos.X = 2 * (y + 18);
pos.Y = x + 1;
SetConsoleCursorPosition(GetStdHandle(STD_OUTPUT_HANDLE), pos);
}
void check2(int x, int y){
int k = 0, kx, ky, f = 1;
for (int i = 0; i <= 3; i++){
if (b2[x + fx[i][0]][y + fx[i][1]] == 2) k = i;
if (b2[x + fx[i][0]][y + fx[i][1]] == 1) f = 0;
}
for (kx = x, ky = y; b2[kx][ky] == 2; kx += fx[k][0], ky += fx[k][1]);
if (b2[kx][ky] == 1) f = 0;
if (f){
int w = 0;
color(12);
for (kx = x, ky = y; b2[kx][ky] == 2; kx += fx[k][0], ky += fx[k][1]){
gotoxy2(kx, ky);
a2[kx][ky] = "※";
c2[kx][ky] = 12;
cout << "※";
w++;
}
for (kx = x + fx[(k + 2) % 4][0], ky = y + fx[(k + 2) % 4][1]; b2[kx][ky] == 2; kx += fx[(k + 2) % 4][0], ky += fx[(k + 2) % 4][1]){
gotoxy2(kx, ky);
a2[kx][ky] = "※";
c2[kx][ky] = 12;
cout << "※";
w++;
}
if (w>0){
rest[2][w]--;
r2--;
if (rest[2][w]>0) color(14); else color(11);
gotoxy2(6 - w, 17); printf("*%d", rest[2][w]);
}
}
}
int move1(){
if (r1*r2 == 0) return(1);
color(5); gotoxy1(14, 4); printf("电脑开炮");
color(13); gotoxy2(14, 4); printf("玩家开炮");
int kx = now[1][0], ky = now[1][1], lastx, lasty, f = 1;
char ch;
gotoxy2(kx, ky); color(11); if (a2[kx][ky] != " ")cout << a2[kx][ky]; else cout << "▂"; gotoxy2(kx, ky);
while (f){
ch = _getch();
if (ch == '1' || ch == 'a'){ kx = now[1][0] + fx[2][0]; ky = now[1][1] + fx[2][1]; }
if (ch == '2' || ch == 's'){ kx = now[1][0] + fx[1][0]; ky = now[1][1] + fx[1][1]; }
if (ch == '3' || ch == 'd'){ kx = now[1][0] + fx[0][0]; ky = now[1][1] + fx[0][1]; }
if (ch == '5' || ch == 'w'){ kx = now[1][0] + fx[3][0]; ky = now[1][1] + fx[3][1]; }
if (kx>0 && kx <= 10 && ky>0 && ky <= 10){
gotoxy2(now[1][0], now[1][1]); color(c2[now[1][0]][now[1][1]]); cout << a2[now[1][0]][now[1][1]];
gotoxy2(kx, ky); color(11); if (a2[kx][ky] != " ")cout << a2[kx][ky]; else cout << "▂"; gotoxy2(kx, ky);
now[1][0] = kx; now[1][1] = ky;
}
if ((ch == '0' || ch == ' ') && b2[kx][ky] <= 1){
if (b2[kx][ky] == 1){ b2[kx][ky] = 2; a2[kx][ky] = "◎"; c2[kx][ky] = 4; }
if (b2[kx][ky] == 0){ b2[kx][ky] = 4; a2[kx][ky] = " "; }
gotoxy2(kx, ky); color(c2[kx][ky]); cout << a2[kx][ky];
f = 0;
check2(kx, ky);
color(7); gotoxy2(12, 4); cout << "("; color(6); cout << ky; color(7); cout << ","; color(2); cout << kx; color(7); cout << ") ";
if (b2[kx][ky] == 2) move1();
}
if (ch == '8' || ch == 'g'){
for (int i = 1; i <= 10; i++) for (int j = 1; j <= 10; j++)
if (b2[i][j] == 1){
gotoxy2(i, j);
color(10);
printf("Ω");
}
char ccc = _getch();
for (; ccc != '8' && ccc != 'g'; ccc = _getch());
for (int i = 1; i <= 10; i++)for (int j = 1; j <= 10; j++){
gotoxy2(i, j);
color(c2[i][j]);
cout << a2[i][j];
}
gotoxy2(kx, ky); color(11); if (a2[kx][ky] != " ")cout << a2[kx][ky]; else cout << "▂"; gotoxy2(kx, ky);
}
if (ch == '4' || ch == 'q') return(0);
}
return(1);
}
int ok(int x, int y){
int nnn = 0;
if (b1[x][y] == 2 || b1[x][y] == 4 || b1[x][y] == 5) return(0);
for (int i = 0; i <= 7; i++){
if (b1[x + fx[i][0]][y + fx[i][1]] == 2) nnn++;
if (b1[x + fx[i][0]][y + fx[i][1]] == 5) return(0);
}
if (nnn>1) return(0);
return(1);
}
void check1(int x, int y) {
int k = 0, kx, ky, f = 1;
for (int i = 0; i <= 3; i++){
if (b1[x + fx[i][0]][y + fx[i][1]] == 2) k = i;
if (b1[x + fx[i][0]][y + fx[i][1]] == 1) f = 0;
}
for (kx = x, ky = y; b1[kx][ky] == 2; kx += fx[k][0], ky += fx[k][1]);
if (b1[kx][ky] == 1) f = 0;
if (f){
int w = 0;
color(12);
for (kx = x, ky = y; b1[kx][ky] == 2; kx += fx[k][0], ky += fx[k][1]){
gotoxy1(kx, ky);
b1[kx][ky] = 5;
a1[kx][ky] = "※";
c1[kx][ky] = 12;
cout << "※";
w++;
}
for (kx = x + fx[(k + 2) % 4][0], ky = y + fx[(k + 2) % 4][1]; b1[kx][ky] == 2; kx += fx[(k + 2) % 4][0], ky += fx[(k + 2) % 4][1]){
gotoxy1(kx, ky);
b1[kx][ky] = 5;
a1[kx][ky] = "※";
c1[kx][ky] = 12;
cout << "※";
w++;
}
if (w>0){
rest[1][w]--;
r1--;
if (rest[1][w]>0) color(14); else color(11);
gotoxy1(6 - w, -5);
printf("%d*", rest[1][w]);
}
}
}
void move2(){
if (r1*r2 == 0) return;
color(13); gotoxy1(14, 4); printf("电脑开炮");
color(5); gotoxy2(14, 4); printf("玩家开炮");
Sleep(750);
int kx = 0, ky = 0, over = 0;
while (tail>head){
head++;
kx = fd[head][0]; ky = fd[head][1];
if (ok(kx, ky)){ over = 1; break; }
}
while (!over){
kx = rand() % (10) + 1;
ky = rand() % (10) + 1;
if (ok(kx, ky)) over = 1;
}
if (b1[kx][ky] == 1){ b1[kx][ky] = 2; a1[kx][ky] = "◎"; c1[kx][ky] = 4; }
if (b1[kx][ky] == 0){ b1[kx][ky] = 4; a1[kx][ky] = " "; }
gotoxy1(kx, ky); color(11); printf("⊕"); Sleep(600);
gotoxy1(kx, ky); color(c1[kx][ky]); cout << a1[kx][ky];
color(7); gotoxy1(12, 4); cout << "("; color(6); cout << ky; color(7); cout << ","; color(2); cout << kx; color(7); cout << ") ";
check1(kx, ky);
if ((b1[kx][ky] == 2 || b1[kx][ky] == 5) && r1*r2>0){
int i = rand() % (4);
for (int ii = 0; ii <= 3; ii++){
int px = kx + fx[i][0], py = ky + fx[i][1];
if (px>0 && px <= 10 && py>0 && py <= 10){
tail++;
fd[tail][0] = px;
fd[tail][1] = py;
}
i = (i + 1) % 4;
}
move2();
}
}
void put(){
int k = 5;
int num[] = { 0, 0, 1, 2, 1, 1 };
while (k--){
for (int i = 1; i <= num[k+1]; i++){
int f1 = 0, f2 = 0;
int dir1, dir2;
dir1 = rand() % (2);
dir2 = rand() % (2);
while (!f1){
f1 = 1;
int lx = rand() % (10) + 1;
int ly = rand() % (10) + 1;
for (int nx = lx - 1; nx <= lx + fx[dir1][0] * k + 1; nx++)
for (int ny = ly - 1; ny <= ly + fx[dir1][1] * k + 1; ny++)
if (b1[nx][ny] == 1){ f1 = 0; break; }
for (int nx = lx; nx <= lx + fx[dir1][0] * k; nx++)
for (int ny = ly; ny <= ly + fx[dir1][1] * k; ny++)
if (b1[nx][ny] == 3){ f1 = 0; break; }
if (f1){
for (int jx = lx, jy = ly; jx <= lx + fx[dir1][0] * k && jy <= ly + fx[dir1][1] * k; jx += fx[dir1][0], jy += fx[dir1][1]){
b1[jx][jy] = 1;
c1[jx][jy] = 15;
color(15);
gotoxy1(jx, jy); printf("□");
}
}
}
while (!f2){
f2 = 1;
int lx = rand() % (10) + 1;
int ly = rand() % (10) + 1;
for (int nx = lx - 1; nx <= lx + fx[dir2][0] * k + 1; nx++)
for (int ny = ly - 1; ny <= ly + fx[dir2][1] * k + 1; ny++)
if (b2[nx][ny] == 1){ f2 = 0; break; }
for (int nx = lx; nx <= lx + fx[dir2][0] * k; nx++)
for (int ny = ly; ny <= ly + fx[dir2][1] * k; ny++)
if (b2[nx][ny] == 3){ f2 = 0; break; }
if (f2){
for (int jx = lx, jy = ly; jx <= lx + fx[dir2][0] * k && jy <= ly + fx[dir2][1] * k; jx += fx[dir2][0], jy += fx[dir2][1])
b2[jx][jy] = 1;
}
}
int a = 1;
}
}
}
void reset(){
system("cls");
color(15); gotoxy(18, 10); printf("按 0 重排战船; 按任意键开始与电脑对战");
color(9);
gotoxy(0, 9); printf("玩家海域");
gotoxy(0, 22); printf("电脑海域");
rest[1][2] = rest[2][2] = 1;
rest[1][3] = rest[2][3] = 2;
rest[1][4] = rest[2][4] = 1;
rest[1][5] = rest[2][5] = 1;
for (int i = 1; i <= 10; i++){
b1[0][i] = b1[i][0] = b2[0][i] = b2[i][0] = 3;
b1[11][i] = b1[i][11] = b2[11][i] = b2[i][11] = 3;
}
color(8);
for (int i = 1; i <= 10; i++)for (int j = 1; j <= 10; j++) c1[i][j] = c2[i][j] = 8;
for (int i = 1; i <= 10; i++)for (int j = 1; j <= 10; j++){
b1[i][j] = b2[i][j] = 0;
a1[i][j] = "□"; gotoxy1(i, j); cout << a1[i][j];
a2[i][j] = "□"; gotoxy2(i, j); cout << a2[i][j];
}
color(14);
gotoxy1(1, -5); printf("%d*□□□□□", rest[1][5]);
gotoxy1(2, -5); printf("%d*□□□□ ", rest[1][4]);
gotoxy1(3, -5); printf("%d*□□□ ", rest[1][3]);
gotoxy1(4, -5); printf("%d*□□ ", rest[1][2]);
gotoxy2(4, 12); printf(" □□*%d", rest[2][2]);
gotoxy2(3, 12); printf(" □□□*%d", rest[2][3]);
gotoxy2(2, 12); printf(" □□□□*%d", rest[2][4]);
gotoxy2(1, 12); printf("□□□□□*%d", rest[2][5]);
color(2); for (int i = 1; i <= 10; i++){ gotoxy1(i, 11); cout << i; gotoxy2(i, 11); cout << i; }
color(6); for (int i = 1; i <= 10; i++){ gotoxy1(11, i); cout << i; gotoxy2(11, i); cout << i; }
color(7); gotoxy1(12, 4); printf("( , )"); gotoxy2(12, 4); printf("( , )");
put();
now[0][0] = now[0][1] = now[1][0] = now[1][1] = 1;
r1 = r2 = 5;
char res = _getch(); if (res == '0') reset();
}
int main(){
int gameover = 1;
while (gameover){
srand(time(NULL));
reset();
gotoxy(18, 10); printf(" ");
int haha = 0;
while (r1*r2){
if (!move1()){ haha = 1; break; } //玩家(haha==1说明中途退出)
move2(); //电脑
}
gotoxy(18, 0);
if (haha) printf("怎么中途退出了...\n\n");
else if (r1 == 0) printf("很遗憾,你输了...\n\n");
else if (r2 == 0) printf("恭喜你,你赢了!!!\n\n");
printf("按1退出; 按其它键继续\n>>");
if (_getch() == '1') gameover = 0;
}
}
习题3.3
6.奇数派游戏 在操场上有n>=3个人,每人都有唯一一位最近的邻居。他们手上都有一块奶油派,收到信号后,都会把派扔向他最近的邻居。假设n是奇数,而且每个人都扔的很准。请判断对错:至少有一个人不会被奶油派击中。
解答:判断正确,可以用数学归纳法证明。当n等于3时,首先寻找一个最近对,他们互相扔奶油派,剩余一人无论扔谁,自己都不会被扔;当n=k时判断成立,那么当n=k+2时,首先找到一个最近对,他们互相扔奶油派。剩余的k个人,如果他们没有人扔向最近的两人,问题转化为n=k的情况,判断成立;如果剩余的k个人中有x个人(x>=1)扔向了最近对中的一个人,那么还剩余k - x个奶油派,还剩余k个人需要判断是否被扔,显然不是所有人都能被扔到,判断成立,数学归纳法得证。
习题3.4
9.八皇后问题 这是一个经典游戏:在一个8*8的棋盘上,摆放8个皇后使得任意两个皇后不在同一行或者同一列或者同一对角线上。那么对下列各种情形,各有多少种不同的摆放方法?
a.任意两个皇后不在同一块方格上。
解答:C_6^48=4426165368
b.任意两个皇后不在同一行上。
解答:![]()
c.任意两个皇后不在同一行或者同一列上。
解答:8!= 40320
同时估计在每秒能检查100亿个位置的计算机上,穷举查找针对上述情形找到问题的所有解需要多少时间。
解答:![]()
10.幻方问题 n阶幻方是把从1到n2的整数填入一个n阶方阵,每个整数只出现一次,使得每一行、每一列、每一条主对角线上的各数之和都相等。
a. 证明:如果n阶幻方存在的话,所讨论的这个和一定等于n(n2+1)/2。
解答: 假设存在n阶幻方,那么n行或者n列的和都相同,这个和等于(1+n2)×n22÷n![]() = n(n2+1)/2
= n(n2+1)/2
b. 设计一个穷举算法,生成阶数为n的所有幻方。
解答:不断生成1到n2的排列,依次填入n阶方阵,检查是否满足幻方要求。
c. 在因特网上或者图书馆查找一个更好的生成幻方的算法。
解答:奇数阶幻方最经典的填法是罗伯法。填写的方法是:把1(或最小的数)放在第一行正中; 按以下规律排列剩下的(n×n-1)个数:
1、每一个数放在前一个数的右上一格;
2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;
5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
双偶数阶幻方用对称交换法。所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即 n×n+1),我们称它们为一对互补数 。如在三阶幻方中,每一对和为 10 的数,是一对互补数 ;在四阶幻方中,每一对和为 17 的数,是一对互补数 。
单偶数阶幻方用象限对称交换法。阶数n满足:n=4*k+2。此处以n=10为例,10=4×2+2,则k=2。
(1)把方阵分为A,B,C,D四个象限,这样每一个象限都是奇数阶。用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2)从A象限的中间行、中间格开始,按自左向右的方向,标出k格。A象限的其它行则标出最左边的k格。将这些格,和C象限相对位置上的数互换位置。
(3)从B象限的最中间列开始,自右向左,标出k-1列。(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换), 将B象限标出的这些数,和D象限相对位置上的数进行交换,就形成幻方。
d. 实现这两个算法——穷举查找算法以及在因特网上找的算法,然后在自己的计算机上做一个试验,确定在一分钟之内,这两个算法能够求出的幻方的最大阶数n。
//穷举法打印n阶魔方矩阵 n <= 10
#include < iostream >
#include < conio.h >
using namespace std;
int A[11][11];
bool Flag[101]; //若K已被使用则Flag[k]=true,否则为false
int n = 3, Count = 0, Point = 0, Avr = 0;
int i_g = 1, j_g = 1, k_g = 1;
bool i_change = false;
bool j_loop = false, k_loop = false;
/funtion init( )
void init() // 对变量初始化
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
A[i][j] = 0;
Flag[j + (i - 1) * n] = false;
}
Count = n * n; // 矩阵的变量数
Point = n / 2; // 设置判断点
for (int i = 1; i <= Count; i++)
Avr += i;
Avr /= n; // 矩阵每行每列之和必须 = Avr
}
funtion Sum( )
int Sum(int j, bool row)
{
int total = 0;
if (row == true) // 返回 j个数的最大之和(末被使用的)
for (int k = Count; j; k--)
{
if (!Flag[k])
{
total += k;
j--;
}
}
else if (row == false) // 返回 j个数的最小之和......
for (int k = 1; j; k++)
{
if (!Flag[k])
{
total += k;
j--;
}
}
return Avr - total;
}
/function Test( )
bool Test(int i, int j) //测试A[i][j]是否可行,可行返回true,否则false
{
int temp;
if (j > Point)
{
temp = 0;
for (int k = j; k >= 1; k--)
temp += A[i][k]; //计算第i行元素之和(被使用的)
if (j == n && temp != Avr)
return false;
else if (j != n && (temp < Sum(n - j, true) || temp > Sum(n - j, false)))
return false;
}
if (i > Point)
{
temp = 0;
for (int k = i; k >= 1; k--)
temp += A[k][j]; // 计算第j列元素之和(被使用的)
if (i == n && temp != Avr)
return false;
else if (i != n && (temp < Sum(n - i, true) || temp > Sum(n - i, false)))
return false;
}
temp = 0;
if (i == n && j == 1) // A[i][j]为左下角的元素
{
for (int a = i, b = j; a >= 1; a--, b++)
temp += A[a][b]; // 计算左斜线的元素之和(已全部使用)
if (temp == Avr)
return true;
else
return false;
}
if (i == n && j == n) // A[i][j]为右下角的元素
{
for (int a = i, b = j; a >= 1; a--, b--)
temp += A[a][b]; // 计算右斜线的元素之和(已全部使用)
if (temp == Avr)
return true;
else
return false;
}
temp = 0;
if (i == j)
{
for (int a = i, b = j; a >= 1; a--, b--)
temp += A[a][b]; // 计算右斜线的元素之和(被使用的)
if (temp < Sum(n - i, true) || temp > Sum(n - i, false))
return false;
}
temp = 0;
if (i + j == n + 1)
{
for (int a = i, b = j; a >= 1; a--, b++)
temp += A[a][b]; // 计算右斜线的元素之和(被使用的)
if (temp < Sum(j - 1, true) || temp > Sum(j - 1, false))
return false;
else
return true;
}
return true;
}
/function back()
bool back() // 进行回溯
{
if (j_g == 1)
{
j_loop = false;
Flag[A[i_g - 1][n - 1]] = false;
Flag[A[i_g - 1][n]] = false;
k_g = A[i_g - 1][n - 1];
A[i_g - 1][n] = -1;
A[i_g - 1][n - 1] = -1;
i_g--;
i_change = true;
j_g = n - 1;
if (k_g == Count) //如果A[ i_g - 1 ][ n - 1]取的已是最后一个元素,则再进行一次回溯
back();
}
else
{
Flag[A[i_g][j_g - 1]] = false;
k_g = A[i_g][j_g - 1];
A[i_g][j_g - 1] = -1;
j_g--;
if (k_g == Count)//如果A[ i_g ][ j_g - 1]取的已是最后一个元素,则再进行一次回溯
back();
}
return true;
}
//function Work( )
void Work()
{
for (; i_g <= n; i_g++)
{
j_loop = true;
for (; j_g <= n && j_loop; j_g++)
{
k_loop = true;
for (; k_g <= Count && k_loop; k_g++)
{
if (Flag[k_g]) //k已被使用
{
if (k_g == Count) //不能再取值了,进行回溯
{
back();
j_g--;
if (i_change)
{
i_g--;
j_loop = false;
}
k_loop = false;
i_change = false;
}
else // 取值末到末尾,考虑下一个元素
continue;
}
else // k末被使用。
{
A[i_g][j_g] = k_g; // 赋值
Flag[k_g] = true; // 标志K已被使用
if (i_g > Point || j_g > Point) // 超过判断点进行判断
{
if (!Test(i_g, j_g)) // A[i][j]不可取
{
A[i_g][j_g] = -1; // 取消赋值
Flag[k_g] = false; // 取消标志
if (k_g != Count) // 取值末到末尾,考虑下一个元素
continue;
else // 取值到末尾,不能再取了,进行回溯
{
back();
j_g--;
if (i_change)
{
i_g--;
j_loop = false;
}
k_loop = false;
i_change = false;
}
}
else // A[i][j]可取
{
if (j_g == n) // 如果j循环到末尾,则从头开始取值
{
j_g = 0;
k_g = 0;
k_loop = false;
j_loop = false;
}
else // j末到末尾
{
k_loop = false;
k_g = 0;
}
}
}
else // 末超过判断点
{
if (j_g == n) // 如果j循环到末尾,则从头开始取值
{
j_g = 0;
k_g = 0;
k_loop = false;
j_loop = false;
}
else // j末到末尾
{
k_loop = false;
k_g = 0;
}
}
}
} // end k_g
} // end j_g
} // end i_g
}
void main()
{
cout << "Please input n:";
cin >> n;
init();
Work();
for (int i = 1; i <= n; i++) // 打印矩阵
{
for (int j = 1; j <= n; j++)
cout << " " << A[i][j];
cout << endl;
}
_getch();
} 一分钟最多能计算4阶幻方
#include
#include
#include
#include
using namespace std;
#define maxn 1000
int m[maxn][maxn];
void OddMagic(int n) //奇数阶幻方
{
memset(m, 0, sizeof(m)); //幻方清零
int x = 0, y = n / 2;
for (int i = 1; i <= n*n; i++)
{
m[x][y] = i;
x--; //依次沿右上角填充
y++;
if (x<0 && y>n - 1) { x = x + 2; y = y - 1; } //沿对角线超出
else if (x<0) x = x + n; //沿上边界超出
else if (y>n - 1) y = y - n; //沿右边界超出
else if (m[x][y] != 0) { x = x + 2; y = y - 1; } //右上角已填充
}
}
void DoubleEvenMagic(int n) //双偶数阶幻方
{
memset(m, 0, sizeof(m)); //幻方清零
for (int i = 1, x = 0, y = 0; i <= n*n; i++) //依次按顺序赋初值
{
m[x][y] = i;
y++;
if (y>n - 1) { x++; y -= n; }
}
for (int i = 0; in0 + n0 / 2 - (k - 1); j--)
swap(m[i][j], m[i + n0][j]); //将右上角幻方最中间列起从右向左的k-1列元素与右下角幻方相应位置元素交换
}
bool Check(int n)
{
int cnt = n*(n*n + 1) / 2; //每行每列以及对角线之和
for (int i = 0; i> n)
{
if (n<3) cout << "Impossible" << endl;
else if (n & 1) { OddMagic(n); if (Check(n)) print(n); } //输出奇数阶幻方
else if (!(n % 4)) { DoubleEvenMagic(n); if (Check(n)) print(n); } //输出双偶数阶幻方
else { SingleEvenMagic(n); if (Check(n)) print(n); } //输出单偶数阶幻方
}
return 0;
} 打印n=1000时的幻方所需时间约为1分钟
11.字母算术 有一种称为密码算术的算式谜题,它的算式中,所有的数字都被字母所代替。如果该算式中的单词是有意义的,那么这种算式被称为字母算式题。最著名的字母算式是由大名鼎鼎的英国谜题大师亨利·E.杜德尼给出的:
这里有两个假设:第一,字母和十进制数字之间是一一对应的关系,也就是说,每个字母只代表一个数字,而且不同的字母代表不同的数字;第二,数字0不出现在任何数的最左边。求解一个字母算数意味着找到每个字母代表的是哪个数字。请注意,解可能并不是唯一的,不同人的解可能并不相同。
a. 写一个程序用穷举查找解密码算术谜题。假设给定的算式是两个单词的加法算式。
#include
bool func(int s, int e, int n, int d, int m, int o, int r, int y)
{
int hash[10] = { 0 };
hash[s]++;
hash[e]++;
hash[n]++;
hash[d]++;
hash[m]++;
hash[o]++;
hash[r]++;
hash[y]++;
for (int i = 0; i < 10; i++)
{
if (hash[i] > 1)
return false;
}
return true;
}
int main()
{
int s,e,n,d,m,o,r,y;
int sum1, sum2, sum3;
for (s = 1; s<10; s++)
{
for (e = 0; e<10; e++)
{
for (n = 0; n < 10; n++)
{
for (d = 0; d < 10; d++)
{
for (m = 1; m < 10; m++)
{
for (o = 0; o < 10; o++)
{
for (r = 0; r < 10; r++)
{
for (y = 0; y < 10; y++)
{
sum1 = s * 1000 + e * 100 + n * 10 + d;
sum2 = m * 1000 + o * 100 + r * 10 + e;
sum3 = m * 10000 + o * 1000 + n * 100 + e * 10 + y;
if (sum1+sum2 == sum3&&func(s, e, n, d, m, o, r, y))
{
printf(" %d%d%d%d\n", s, e, n, d);
printf(" +%d%d%d%d\n", m, o, r, e);
printf("=%d%d%d%d%d\n", m, o, n, e, y);
}
}
}
}
}
}
}
}
}
return 0;
} b. 杜德尼的谜题发表于1924年,请用你认为合理的方法解该谜题。
解答:首先加法的进位最多1,所以M=1 那么M+S要进位至少为10,而百位最多能给一个进位,那么S=9或者8。假设S为8 根据刚才推断此时千位为10,进1后剩余0,所以O为0,O为0的话E也必须是9才能进位,则进位剩余为0,则N=0 矛盾。并且十位的N=0和R必须进位且剩余E=8,也不可能矛盾。所以S=9。同样此时O就可能为0或者1,因为M已经等于1,所以O=0,现在百位E+O(O=0)(可能有进位)=N,因为E≠N 所以十位必须有进位,则N=E+1。那么N+R=E+10或者N+R+1=E+10,则R必须为8或者9,因为S已经为9,所以R只能为8,那么个位也必须进位了,可知 D+E=10+Y。这个时候从选择E入手(使得D,E,N,Y都不同,且D+E=10+Y ,N=E+1,而且不能为已有的9(S),8(R),0(O),1(M))结合以上条件就可以得出E=5,其余也出来了。
习题3.5
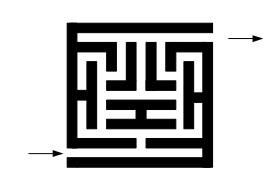
10.我们可以用一个代表起点的顶点、一个代表重点的顶点、若干个代表死胡同和通道的顶点来对迷宫建模,迷宫中的通道不止一条,我们必须求出连接起点和终点的迷宫道路。
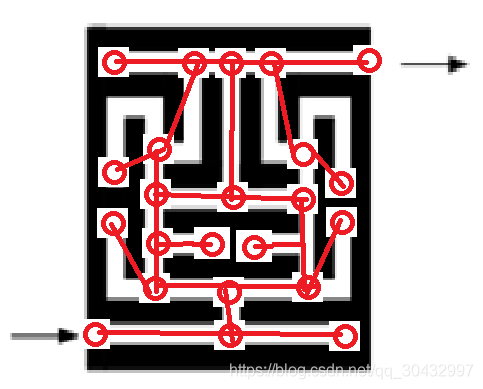
a.为下图的迷宫构造一个图。
b.如果你发现自己身处一个迷宫中,你会选用DFS遍历还是BFS遍历?为什么?
解答:我会选择DFS遍历。深度优先遍历过程中,每次遇到走不通的节点,则回溯到上一个节点,继续进行深度优先搜索,一旦找到出口就结束了。而广度优先搜索具有层次的概念,需要遍历完当前节点的所有的相邻节点,这在走迷宫的时候相当于走了很多回头路,效率相比深度优先搜索而言很差。
11.三壶问题 西蒙·丹尼斯·泊松是著名的法国数学家和物理学家。据说在他遇到某个古老的谜题之后,就开始对数学感兴趣了,这个谜题是这样的:给定一个装满水的8品脱壶以及两个容量分别为5品脱和3品脱的空壶,如何通过完全灌满或者倒空这些壶从而使得某个壶精确地装有4品脱的水?用广度优先查找来解这个谜题。
分析:解法:可以把每次三个水壶中水的量组成一个状态,比如初始状态为008,对应第一个水壶0品脱水,第二个水壶0品脱水,第三个水壶8品脱水。对题目的状态空间图进行广度优先遍历。当表示状态的数字中出现4时,即求出答案。
1、为了打印出倒水的过程,需要声明一个前置状态保存当前状态由哪个状态转换而来,然后就可以回溯到初始状态,打印出倒水过程。相当于树中的父结点。
2、可以声明一个map表,保存已有的状态,对已有的状态,就不再向下继续遍历,这样可以节省求解时间。
3、因为是广度优先遍历,所以第一次解得的答案所需的倒水的次数最少,解为最优解。
#include
#include
#include