动态规划总结——线性DP(买卖股票系列)(基于LeetCode题目)
LeetCode动态规划题目汇总
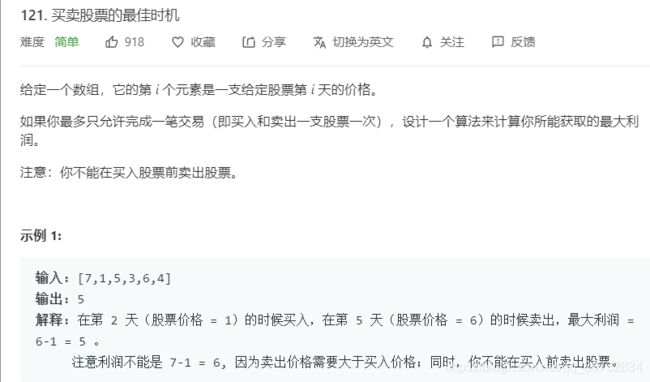
首先解构下问题,要找利益最大,也就是买入和卖出的正差值最大,那么我们需要记录下历史的最低价(截至i天,最低的价格),然后再与每次新的售价进行对比如果更低更新历史最低价,如果比之大则判断是不是大到比最低价之后的最高价还大了(就是差值有没有之前算的大。)
dp[i]记录第i天的历史最低价。
转移方程:
dp[i] = min(dp[i-1],prices[i])
然后找出最大的售价即可。
这个空间也很好优化,最低售价仅与昨天的最低售价有关,最高卖出价同理,且买入当天不能卖出,更低的售价也不可能作为卖出价。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<2){
return 0;
}
int min =prices[0],max = 0;
for(int i=1;i<prices.length;i++){
int temp = prices[i]-min;
if(temp<0){
min = prices[i];
}else if(temp>max){
max = temp;
}
}
return max;
}
}

与上题不同的是,可以多次交易,那见钱就卖,赚了再说嘛,卖了当天假装买入如果有更低价格更新价格,如果没有后面遇到比较大价值的也相当于我们还持有该股票且以之前卖出价格买入了,之间加起来结果一样的。
定义啊转移与之前一样,不过多了一个,卖出当天将最低价重置为卖出那天
dp[i] = 没有卖,min(dp[i-1],prices[i]),卖,prices[i];
发现没有,不卖的条件是差值小于0,卖的条件是大于0,那么可以当作每天都是最低价(滑稽)
class Solution {
public int maxProfit(int[] prices) {
int ans = 0,buy=prices[0];
for(int i=1;i<prices.length;i++){
int temp = prices[i]-buy;
if(temp>0){
ans += temp;
}
buy = prices[i];
}
return ans;
}
}
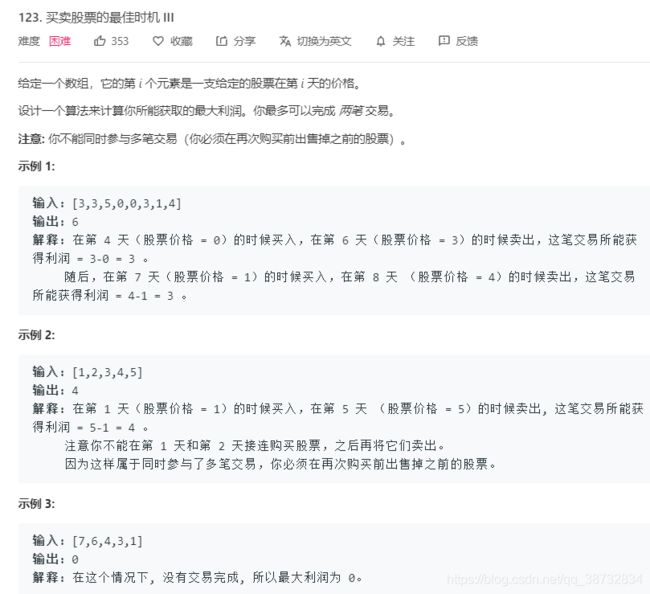
再抽象一下前两题,之前第一题其实是求一个最大的的点和在它之前最低的点,中间的过程都不比管。就是如图所示的两个点
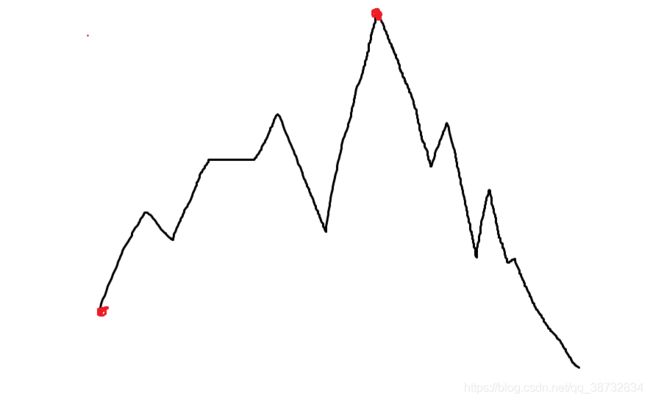
第二次则是找出所有上升区间全部相加。

红色是第一次交易的收益走势,可以知道如果一直是上升情况下,无论几次收益结果都是一样的,只有当遇到直线时,且对应每天价格走势图,只有有其他上升区间价格才会变化,所以我们可以采取通过这种方式划分区间…我们只需要记录下最大的两个上升区间
用动规的方式做,首先定义状态,我们这次保存收益。
dp[j][i]:j次交易后,第i天最大为收益是多少
min:还需要一个值来记录本轮交易的最小成本,注意不是历史最低售价了
状态转移方程:
min:min(昨天本轮交易的最低成本,今天的售价-上一轮交易的今日的收益(成本))
dp[j][i] = max(今天卖,昨天的收益) 今天卖=今日售价-min
初始化,第一天最低肯定是0收入啊,0次交易肯定是零收入啊。
肯定有同学有个问题,这样会不会同一时间段重复交易啊,当然不会,虽然操作上会,但是结果不会,再看看我上面的灵魂画作,只有当在上一次交易额为直线时(也就是非区间范围),且遇到上升区间本轮交易额才会变化(毕竟不做赔本买卖)。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<2){
return 0;
}
int[][] dp = new int[3][prices.length];
int min;
for(int j=1;j<dp.length;j++){
min = prices[0];
for(int i=1;i<prices.length;i++) {
min = Math.min(min, prices[i] - dp[j - 1][i - 1]);
dp[j][i] = Math.max(prices[i]-min,dp[j][i-1]);
}
}
return dp[dp.length-1][dp[0].length-1];
}
}

这题与上题类似,把2换成k而已,不过有个细节,当k大于prices.length/2时就等价为无穷次交易。
class Solution {
public int maxProfit(int k, int[] prices) {
if(prices.length<2){
return 0;
}
if(k>prices.length/2){
return maxProfit(prices);
}
int[][] dp = new int[k+1][prices.length];
int min;
for(int j=1;j<dp.length;j++){
min = prices[0];
for(int i=1;i<prices.length;i++) {
min = Math.min(min, prices[i] - dp[j - 1][i - 1]);
dp[j][i] = Math.max(prices[i]-min,dp[j][i-1]);
}
}
return dp[dp.length-1][dp[0].length-1];
}
private int maxProfit(int[] prices) {
int ans = 0,buy=prices[0];
for(int i=1;i<prices.length;i++){
int temp = prices[i]-buy;
if(temp>0){
ans += temp;
}
buy = prices[i];
}
return ans;
}
}

服了,还是用大佬的方式吧
首先我们,有两种状态,持有股票,售出股票,我们只需要穷举出所有可能的情景便可以得到我们想要的最大值了,再具体一点就是,第i天最大允许交易k次再现在还(持有/卖出)股票的情况下,我们最大收益为多少(虽然正常情况下最大收益,持有是不可能持有的。)
定义: dp[i][k][j] 第i天保证k次交易j状态下,收益情况
转移方程 dp[i][j][持有] = max(dp[i-1][j][持有],dp[i-1][j-1][不持有]-今日售价)
dp[i][j][不持有] = max(dp[i-1][j-1][持有]+今日售价,dp[i-1][j][不持有])
初始化:
0天 全是0
0次交易 全是0
第1天一次交易,持有 -今日售价(dp[1][1][0] =-prices[0])
第1天 一次交易,不持有 0(dp[1][1][1] = 0)
针对这道题多了个冷藏期,持有,要么昨天没卖,要么是昨天以前卖的,不持有的状态不变。
而且是不限制交易次数,那我们每天都交易好不好233333(当然不做赔本买卖)
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<2){
return 0;
}
int[][] dp = new int[prices.length+1][2];
dp[1][0] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[i+1][0] = Math.max(dp[i][0],dp[i-1][1]-prices[i]);
dp[i+1][1] = Math.max(dp[i][0]+prices[i],dp[i][1]);
}
return dp[prices.length][1];
}
}
又应了那句话,状态选得好,代码交得早。
来优化空间,看这里事实上只需要昨天的持有状态,前天的非持有状态,昨天的非持有状态。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<2){
return 0;
}
int have = -prices[0],
pre_no = 0,
no = 0;
for(int i=1;i<prices.length;i++){
int temp = no;
no = Math.max(have+prices[i],no);
have = Math.max(have,pre_no-prices[i]);
pre_no = temp;
}
return no;
}
}
class Solution {
public int maxProfit(int[] prices, int fee) {
int have = -prices[0],no = 0;
for(int i=0;i<prices.length;i++){
have = Math.max(have,no-prices[i]);
no = Math.max(no,have+prices[i]-fee);
}
return no;
}
}
