【算法分析与设计】图:bellman-ford算法
前半部分内容参考自这篇博客
文章目录
- 介绍
- 算法过程
- JAVA实现
- 例题
介绍
Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法。该算法由 Richard Bellman 和 Lester Ford 分别发表于 1958 年和 1956 年,而实际上 Edward F. Moore 也在 1957 年发布了相同的算法,因此,此算法也常被称为 Bellman-Ford-Moore 算法。
Bellman-Ford 算法和 Dijkstra 算法同为解决单源最短路径的算法。对于带权有向图 G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而 Bellman-Ford 算法能适应一般的情况(即存在负权边的情况)。一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。
Bellman-Ford 算法采用动态规划(Dynamic Programming)进行设计,实现的时间复杂度为 O(V*E),其中 V 为顶点数量,E 为边的数量。Dijkstra 算法采用贪心算法(Greedy Algorithm)范式进行设计,普通实现的时间复杂度为 O(V2),若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)。
算法过程
假设图中的顶点A, B, C, D, E,求顶点A到其他顶点的最短距离。首先初始化A到其他顶点的距离为无穷大,同时初始化一个待处理顶点库为【A】:
距离表:
| A | B | C | D | E |
|---|---|---|---|---|
| 0 | ∞ | ∞ | ∞ | ∞ |
顶点库:【A】
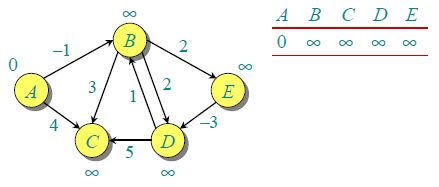
处理顶点库中的顶点A:顶点A与B C相邻,它到另外两个节点的距离分别是-1,4均小于∞,故更新距离表,并将顶点B、C加入到顶点库中:
距离表
| A | B | C | D | E |
|---|---|---|---|---|
| 0 | -1 | 4 | ∞ | ∞ |
顶点库
【B,C】
处理顶点库中的顶点B:顶点B与C,D,E相邻,距离分别为3,2,2。由于A-B-C这条路径比A-C这条路径耗时短,故更新顶点C的距离表,同时更新顶点D和E在距离表中的数据,并将顶点D、E加入到顶点库:
距离表
| A | B | C | D | E |
|---|---|---|---|---|
| 0 | -1 | 2 | 1 | 1 |
顶点库
【C、D、E】
处理顶点库中的顶点C:发现C没有通向其他顶点;
更新顶点库为:【D、E】
处理顶点库的顶点D:顶点D通向顶点C,但是对于C来说,经过D的路径比不经过D的路径要费时,所以不做处理;
更新顶点库为:【E】
处理顶点库的顶点E:E通向顶点D,且可以将顶点D的路径成本降低为-2,故更新距离表,并将具有新路径成本的顶点D加入到顶点库中:
路径表:
| A | B | C | D | E |
|---|---|---|---|---|
| 0 | -1 | 2 | -2 | 1 |
顶点库:
【D】
处理顶点库中的订点D:D通向B和C,但是不能将B和C的路径成本进一步降低了,故路径表不更新,同时顶点库中没有其他顶点了,结束整个过程。
JAVA实现
输入:
int[][] weights:二维数组,表示起点、终点及对应的路径权重,例如:
int[][] weights= {
{2,1,1},
{2,3,1},
{3,4,1}
};
表示下面这个图:
![]()
N:表示节点的个数,上面这个图的N为4
K:表示起点
输出:
int[] path:从节点K出发,到其他所有节点的最短路径数组。
例如对于上面的图来说,起点为节点2时,输出的path为:
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 2 |
class Solution {
public int[] bellmanFord(int[][] weights, int N, int K) {
// 由路径权重数组重构这个图
int[][] graph = new int[N+1][N+1];
for(int i=0;i<N+1;i++)
// graph中的路径权重为-1时表示该边不存在
Arrays.fill(graph[i], -1);
for(int[] w: weights)
graph[w[0]][w[1]] =w[2];
// path[i]表示第K到第i个节点时间
int[] path=new int[N+1];
// 初始时,默认起点到起点的时间为0;起点到其他节点的时间为无穷大
Arrays.fill(path, Integer.MAX_VALUE);
path[K] = 0;
// nodes保存等待处理的节点
Queue<Integer> nodes= new LinkedList<>();
nodes.offer(K);
while(nodes.size()>0) {
int curNode= nodes.poll();
for(int i=1;i<=N;i++) {
if(i==curNode||graph[curNode][i]==-1) continue;
int curPath = path[curNode]+graph[curNode][i];
if(curPath<path[i]) {
nodes.offer(i);
path[i] = curPath;
}
}
}
return path;
}
}
例题
leetcode743
解法