【带删除】【带权】【并查集】【模板】 UVA 11987 Almost Union-Find 【对一些集合进行合并，删除某元素，输出某元素所在集合元素个数和总和】

【带删除】【带权】【并查集】 UVA 11987 Almost Union-Find 【对一些集合进行合并，删除某元素，输出某元素所在集合元素个数和总和】

例题：UVA 11987 Almost Union-Find

I hope you know the beautiful Union-Find structure. In this problem, you’re to implement something similar, but not identical.

The data structure you need to write is also a collection of disjoint sets, supporting 3 operations:

1 p q
Union the sets containing p and q. If p and q are already in the same set, ignore this command.

2 p q
Move p to the set containing q. If p and q are already in the same set, ignore this command

3 p
Return the number of elements and the sum of elements in the set containing p.

Initially, the collection contains n sets: {1}, {2}, {3}, …, {n}.

Input
There are several test cases. Each test case begins with a line containing two integers n and m (1<=n,m<=100,000), the number of integers, and the number of commands. Each of the next m lines contains a command. For every operation, 1<=p,q<=n. The input is terminated by end-of-file (EOF). The size of input file does not exceed 5MB.

Output
For each type-3 command, output 2 integers: the number of elements and the sum of elements.

Sample Input
5 7
1 1 2
2 3 4
1 3 5
3 4
2 4 1
3 4
3 3

Output for the Sample Input
3 12
3 7
2 8

Explanation
Initially: {1}, {2}, {3}, {4}, {5}

Collection after operation 1 1 2: {1,2}, {3}, {4}, {5}

Collection after operation 2 3 4: {1,2}, {3,4}, {5} (we omit the empty set that is produced when taking out 3 from {3})

Collection after operation 1 3 5: {1,2}, {3,4,5}

Collection after operation 2 4 1: {1,2,4}, {3,5}

题意：
1 p q 合并p，q所在集合
2 p q 将元素p从p所在集合删除，然后加入到q所在集合
3 p 输出p所在集合的元素个数和总和

AC代码：
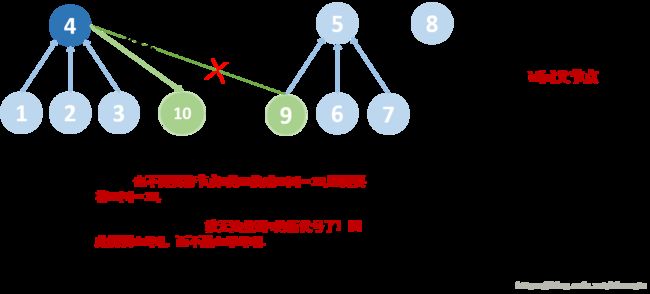
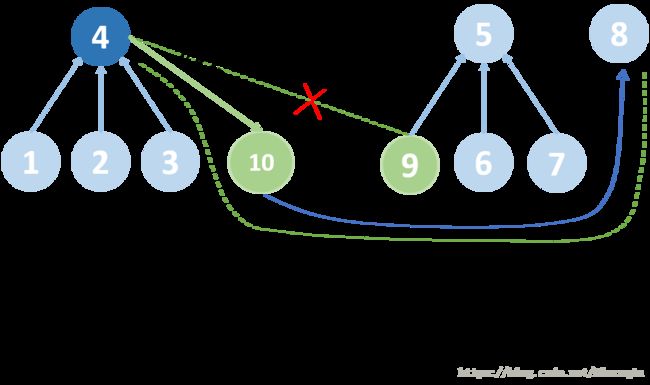
注意合并和删除操作时，是对id[x]进行操作，还是对x直接操作！
只有删除某元素时，才直接使用X，即del(x)！
其他时候，无论是合并，还是查询，都是对id[x]进行操作！

#include 
#include 
#include 

using namespace std;

const int maxn = 100005;
int n, m, dep, fa[maxn], num[maxn], id[maxn];
long long sum[maxn];

void init(int nn)
{
    for(int i = 1; i <= nn; i++)
    {
        fa[i] = i;
        num[i] = 1;
        sum[i] = i;
        id[i] = i;
    }
    dep = nn;
}

int Find(int x)
{
    return x == fa[x] ? x : fa[x] = Find(fa[x]);
}

void Merge(int x, int y)
{
    int fx = Find(x), fy = Find(y);
    if(fx != fy)
    {
        fa[fx] = fy;
        num[fy] += num[fx];
        sum[fy] += sum[fx];
    }
}

void del(int x)
{
    //清理工作
    int fx = Find(id[x]);
    num[fx]--;
    sum[fx] -= x;
    //初始化工作
    id[x] = ++dep;
    sum[id[x]] = x;
    num[id[x]] = 1;
    fa[id[x]] = id[x];
}

int main()
{
    while(~scanf("%d%d", &n, &m))
    {
        init(n);
        while(m--)
        {
            int k, p, q;
            scanf("%d", &k);
            if(k == 1)
            {
                scanf("%d%d", &p, &q);
                //均对id[x]进行操作
                if(Find(id[p]) != Find(id[q]))
                    Merge(id[p], id[q]);
            }
            else if(k == 2)
            {
                scanf("%d%d", &p, &q);
                 //均对id[x]进行操作
                if(Find(id[p]) != Find(id[q]))
                {
                    del(p);//注意！不是del(id[p])
                    Merge(id[p], id[q]);
                }
            }
            else
            {
                scanf("%d", &p);
                 //均对id[x]进行操作
                int fp = Find(id[p]);
                printf("%d %lld\n", num[fp], sum[fp]);
            }
        }
    }
    return 0;
}