Pruning Filters For Efficient ConvNets阅读笔记

问题的提出

现在，神经网络模型在很多领域都展现了强大的性能（如：物体分类，目标识别，物体分割，自然语言处理等）。随着模型性能的提高，网络结构变得越来越深，参数变得越来越多，这就使得保存模型所需要的内存变多，模型进行推理所需要的计算资源与计算时间也变多。但是，在一些嵌入式设备中，内存与计算资源比较匮乏，对系统的实时性要求较高，这就需要对训练好的网络模型进行剪枝，降低保存模型所需要的内存，同时减少模型一次推理所需要的时间。所以，就需要一些方法，在不损失性能（或者损失很少的性能）的前提下，减少网络模型的参数，对模型进行压缩与加速。

在卷积神经网络中，90%的参数都是来自全连接层，但90%的计算都是来自卷积层。在这篇论文之前的一些方法，大多是对全连接层进行剪枝，然后通过权值量化的方法对网络参数进行压缩。这种方法会将网络模型由密集连接转化为稀疏连接，虽然压缩了模型参数，但并不能很好的起到模型推理加速的效果。这篇论文的作者提出了一种新的方法，对神经网络模型的卷积层进行剪枝，这种方法不会产生稀疏矩阵，在压缩网络模型的同时极大的提高了网络推理速度。

难点分析

这篇论文主要是对卷积层进行修剪，不涉及全连接层。修剪卷积层的思路是：找到不重要或者说是冗余的卷积核通道，将这条通道修剪掉。假设我们需要修剪卷积层i，修剪率为20%，这一层在修剪前的输入特征图为$（N,x_i,w_i,h_i）$，卷积核为$（x_{i+1},x_i,k_i,k_i）$，其中：N为输入神经网络的样本数，$x_i$为i层输入特征的通道数，$w_i$和$h_i$代表i层输入特征图的宽和高，$x_{i+1}$为i层卷积核的通道数，k_i为i层卷积核的大小。进行卷积运算后，输出的特征图为$（N,x_{i+1},w_i,h_i）$。修剪后i层输入特征图为$（N,x_i,w_i,h_i）$，卷积核为（80%$x_{i+1},x_i,k_i,k_i$），输出的特征图为（N,80%$x_{i+1},w_i,h_i$）。因为输出特征图通道数发生改变，所以对i+1层的卷积核也会产生影响，由修剪前的$（x_{i+2},x_{i+1},k_{i+1},k_{i+1}）$变为修剪后的（$x_{i+2}$,80%$x_{i+1},k_{i+1},k_{i+1}$）。修剪前后特征图与卷积核大小的变化如下表所示：

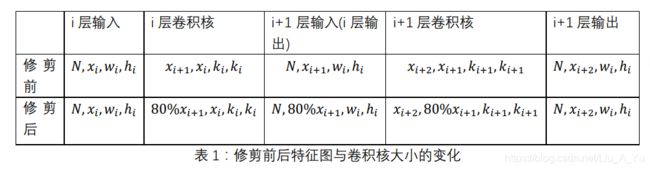
由表1可以得到，对i层的卷积核进行修剪，会对本层的输出产生影响，从而影响下一层(i+1)的卷积核，但对下下层(i+2)层的输出不会影响。
通过上限的分析，这篇论文有三个难点：
1） 每一层的卷积核的修剪率如何确定；
2） 如何确定i层卷积核中哪个通道是不重要的；
3） 某一层卷积核通道的改变会影响下一层的卷积核，在多层剪枝中，如何确定修剪策略。

解决方案

作者采用总体的训练策略仍是经典的三步走策略：
1） 搭建一个神经网络模型，并对神经网络进行完整的训练，获得权重参数；
2） 设置一个剪枝率，在预训练的模型中，将不重要的卷积核通道删除；
3） 对修剪后的网络进行重新训练，补偿网络修剪带来的精度损失，重新训练过程中保留预训练产生的权重，而不是对权重进行随机初始化。

如何确定卷积核通道的重要性
首先计算每个卷积核中，通道的绝对权值之和（即：$l_1$范数），然后对$l_1$范数进行排序，作者认为$l_1$范数越大的通道，对推理结果的贡献度越高，该通道越重要；$l_1$范数越小的通道，对推理结果的贡献度越低，该通道不重要。
为使问题简化，假设某一卷积层i的卷积核大小为（3,1,3,3），共有a,b,c三个通道，每个通道的维度为（1,3,3），如下图所示：

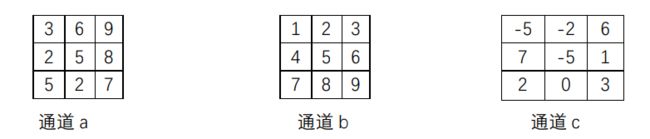
$s_a$= 3 + 6 + 9 + 2 + 5 + 8 + 5 + 2 + 7 = 47
$s_b$= 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
$s_c$= 5 + 2 + 6 + 7 + 5 + 1 + 2 + 0 + 3 = 31
通道重要性排序：$s_c<s_b<s_a$，根据排序结果与想要的修剪率即可对通道进行修剪
同时，作者也与使用了通道的权值平方之和（即：$l_2$范数）作为衡量卷积核中通道重要性的指标，经过试验得出结论，和使用$l_1$范数并没有什么区别。

如何确定每一层的剪枝率

关于如何确定每一层的剪枝率，作者采用的是控制变量法，探索每一个卷积层对剪枝的敏感度。对于敏感度较高的卷积层，剪枝率设置低些甚至可以设置为0，对剪枝敏感度低的卷积层，剪枝率设置高些。
首先，对每一个卷积层进行单独剪枝，以剪枝率为横轴，（剪枝后的准确度/剪枝前的准确度）为纵轴，画出曲线图。若曲线图比较平缓，说明该层对剪枝的敏感度较低，若曲线图比较陡峭，说明对剪枝的敏感度较高。

在多卷积层中如何进行剪枝

在多卷积层中进行剪枝有两种方法：
1） 每一层独立修剪，每修剪一层，后面紧跟一个重训练操作，然后进行下一层的修剪，知道修剪完整个卷积层
2） 将整个网络当成一个整体，修剪完整个网络后在进行重训练操作。
因为，每修剪掉一个卷积核的通道，对下一个卷积层的卷积核也有影响，故修剪策略（计算卷积核通道的重要性）也分为两种：
1） 独立剪枝策略：层与层之间的修剪是相互独立的，互不影响，在计算i+1卷积层通道的重要性时，按修剪前的结构进行计算；
2） 贪心剪枝策略：层与层之间的修剪是相互影响的，在i层修剪后产生的影响会传递到i+1层，在计算i+1卷积层通道的重要性时，按照修剪后的结构进行计算。

具体来说：假设没修剪前i层卷积核大小为（4,5,3,3），i + 1层卷积核大小为（5,3,3,3），采用$l_1$范数算的第4个通道的值最小，重要程度最低，故将其减去，如蓝色部分所示。因为i层卷积核的修剪对i+1层也有影响，则i+1层输入的第四个维度因为上一个卷积层的修剪消失，所以i+1层卷积核也被修剪，如红色部分所示。修剪后i层卷积核变为（4,4,3,3），i+1层卷积核变为（4,3,3,3）。

现在对i+1层进行修剪，若采用独立剪枝策略，进行卷积层通道重要性计算时，不考虑上一卷积层修剪后产生的后果，会连同红色部分一同计算进去；若采用贪心剪枝策略，需要考虑上一卷积层修剪后产生的后果，不会计算红色部分。

论文的优点

针对这篇论文，作者提出了一种卷积核的修剪方法，利用l_1范数来衡量卷积核通道的重要性进行修剪，既压缩了网络模型，也减少了参数之间的计算量。在VGGNet中大约可以减少30%的运算量，并且不会产生精度损失。