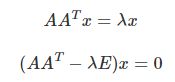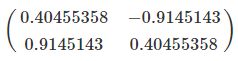奇异值分解 (SVD)原理及python实现
奇异值分解(Singular Value Decomposition,SVD)是一种矩阵分解(Matrix Decomposition)的方法。除此之外,矩阵分解还有很多方法,例如特征分解(Eigendecomposition)、LU分解(LU decomposition)、QR分解(QR decomposition)和极分解(Polar decomposition)等。这篇文章主要说下奇异值分解,这个方法在机器学习的一些算法里占有重要地位。
————————————————————————————————————————————————————————
定义
下面引用 SVD 在维基百科中的定义。
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It is the generalization of the eigendecomposition of a positive semidefinite normal matrix (for example, a symmetric matrix with positive eigenvalues) to any m×nm×n matrix via an extension of polar decomposition.
也就是说 SVD 是线代中对于实数矩阵和复数矩阵的分解,将特征分解从 半正定矩阵 推广到任意 m×nm×n 矩阵。
注意:本篇文章内如未作说明矩阵均指实数矩阵。
假设有 m×nm×n 的矩阵 AA ,那么 SVD 就是要找到如下式的这么一个分解,将 AA 分解为 3 个矩阵的乘积:
其中,UU 和 VV 都是正交矩阵 (Orthogonal Matrix),在复数域内的话就是酉矩阵(Unitary Matrix),即
换句话说,就是说 UU 的转置等于 UU 的逆,VV 的转置等于 VV 的逆:
而 ΣΣ 就是一个非负实对角矩阵。
那么 UU 和 VV 以及 ΣΣ 是如何构成的呢?
_____________________________________________________________________________________________________
求解
UU 和 VV 的列分别叫做 AA 的 左奇异向量(left-singular vectors)和 右奇异向量(right-singular vectors),ΣΣ 的对角线上的值叫做 AA 的奇异值(singular values)。
其实整个求解 SVD 的过程就是求解这 3 个矩阵的过程,而求解这 3 个矩阵的过程就是求解特征值和特征向量的过程,问题就在于 求谁的特征值和特征向量。
- U 的列由
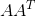 的单位化过的特征向量构成
的单位化过的特征向量构成 - V 的列由
 的单位化过的特征向量构成
的单位化过的特征向量构成 - Σ 的对角元素来源于
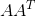 或
或  的特征值的平方根,并且是按从大到小的顺序排列的
的特征值的平方根,并且是按从大到小的顺序排列的
知道了这些,那么求解 SVD 的步骤就显而易见了:
- 求
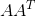 的特征值和特征向量,用单位化的特征向量构成 U
的特征值和特征向量,用单位化的特征向量构成 U - 求
 的特征值和特征向量,用单位化的特征向量构成 V
的特征值和特征向量,用单位化的特征向量构成 V - 将
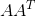 或者
或者  的特征值求平方根,然后构成 Σ
的特征值求平方根,然后构成 Σ
_____________________________________________________________________________________________________
举例
假设
那么可以计算得到
接下来就是求这个矩阵的特征值和特征向量了
要想该方程组有非零解(即非零特征值),那么系数矩阵 ![]() −λE 的行列式必须为 0
−λE 的行列式必须为 0
求解这个行列式我就不再赘述了,这个直接使用行列式展开定理就可以了,可以得到 λ1≈29.86606875,λ2≈0.13393125,λ3=λ4=0,有 4 个特征值,因为特征多项式 |![]() −λE| 是一个 4 次多项式。对应的单位化过的特征向量为
−λE| 是一个 4 次多项式。对应的单位化过的特征向量为
这就是矩阵 U 了。
同样的过程求解 ![]() 的特征值和特征向量,求得 λ1≈0.13393125,λ2≈29.86606875,将特征值降序排列后对应的单位化过的特征向量为
的特征值和特征向量,求得 λ1≈0.13393125,λ2≈29.86606875,将特征值降序排列后对应的单位化过的特征向量为
这就是矩阵 V 了。
而矩阵 Σ 根据上面说的为特征值的平方根构成的对角矩阵
到此,SVD 分解就结束了,原来的矩阵 A 就被分解成了 3 个矩阵的乘积。
____________________________________________________________________________________________________
Numpy 实现
Python 中可以使用 numpy 包的 linalg.svd() 来求解 SVD。