原文首发于https://magicly.me/hpc-julia/
最近有个项目是计算密集型的, 最开始用 TS 快速实现了算法原型, 后来改用 Go 重写, Go 的 goroutine 用起来还是蛮爽的, 很容易把所有 cpu core 跑满。 不过随着代码逐渐复杂, 感觉用 Go 还是没有动态语言写起来爽, 性能也没有达到极致, 跟 C/C++/Rust 还是有一定差距,似乎对 GPU 和 SIMD 支持也不太好(不敢说对 Go 精通, 可能是我没找到合适的打开方式吧)。 一开始打算用 Rust 尝试一下, 之前用过一下, 性能确实可以(毕竟没有 runtime/GC),结果前段时间 Julia 发布 1.0,看了一下语法、性能等各方面都很适合, 遂决定用 Julia 写。
本文记录一下学习 Julia HPC 方面的经历。
使用 Julia
网上有很多 Julia 的教程, 推荐几个大家自己去看看吧:
- https://zhuanlan.zhihu.com/p/...
- 上一篇作者的视频https://www.bilibili.com/vide... , 去 bilibili 上搜索 Julia, 有意外惊喜
- https://benlauwens.github.io/... , 除了 Julia 本身, 关于开发方法、调试等知识也值得看一下
- https://julialang.org/learning/ 这个里面有很多教程, 包括书籍、视频、blog 等
- Jane Herriman 的 Intro to Julia 系列直播可以看一下,https://www.youtube.com/watch... 这个貌似是最新的(每次直播貌似基本上都是一样的内容), 对应的代码在https://github.com/JuliaCompu...
High Performance Computing Julia
主要参考《Julia High Performance》,书里用的 Julia0.4, 很多代码已经跑不起来了, 我参考官网文档修改了一下。 后面有时间会根据官网文档再整理一些 HPC 相关的资料。
测试机器为:
julia> versioninfo()
Julia Version 1.0.1
Commit 0d713926f8 (2018-09-29 19:05 UTC)
Platform Info:
OS: macOS (x86_64-apple-darwin14.5.0)
CPU: Intel(R) Core(TM) i7-4870HQ CPU @ 2.50GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-6.0.0 (ORCJIT, haswell)有多快
参考官网 Benchmark:
让我惊讶的是, LuaJIT 居然比 Rust 还快!!!
为什么如此快
Julia 设计之初就重点考虑了速度, 它的快很大程度上来源于 LLVM, JIT 以及类型设计。 Julia 有类型推断,编译的时候会根据不同 type 生成不同的特定代码,叫 code specialization,然后运行的时候会根据参数类型选择最适合的方法,即 Multiple dispatch。
性能分析工具
没有分析的优化都是耍流氓!
性能分析工具主要有如下几个:
@time
@time sqrt.(rand(1000));输出结果:
julia> @time sqrt.(rand(1000));
0.057799 seconds (187.82 k allocations: 9.542 MiB, 9.82% gc time)
julia> @time sqrt.(rand(1000));
0.000022 seconds (8 allocations: 16.063 KiB)这里;是为了不输入结果值。 因为rand(1000)返回的是一个 vector, sqrt.即可作用于 vector 中的每一个元素, 类似 numpy 中的 broadcast 吧。
注意, 第一次运行的时候 Julia 会编译代码, 所以时间会长很多, 应该以第二次以及之后的为准!
@timev
用法同@time, 功能增加了 memory, 以及时间精确到 ns。
julia> @timev sqrt.(rand(1000));
0.000025 seconds (8 allocations: 16.063 KiB)
elapsed time (ns): 25340
bytes allocated: 16448
pool allocs: 6
non-pool GC allocs:2Julia profiler
用 profiler 可以分析出那段代码占用了最多时间。
using Profile
using Statistics
function testfunc()
x = rand(1000000)
y = std(x)
return y
end
@profile testfunc()Profile 会采样搜集 profile 信息,获取信息:
Profile.print();Profile 的输出不便于分析, 可以采用 ProfileView 输出火焰图(说实话跟 Go 的火焰图差远了):
Pkg.add("ProfileView");
using ProfileView
ProfileView.view()BenchmarkTools
https://github.com/JuliaCI/Be...
julia> Pkg.add("BenchmarkTools")
julia> using BenchmarkTools
julia> @benchmark sqrt.(rand(1000))
BenchmarkTools.Trial:
memory estimate: 15.88 KiB
allocs estimate: 2
--------------
minimum time: 4.935 μs (0.00% GC)
median time: 5.598 μs (0.00% GC)
mean time: 7.027 μs (11.17% GC)
maximum time: 229.810 μs (97.54% GC)
--------------
samples: 10000
evals/sample: 7可以看到,包括内存占用、内存分配次数,运行时间统计等, 我们后面很多实验都是用@benchmark。
Types
Julia 的类型是在 runtime 检查的, 但是在 compile time 会生成不同类型的方法。
Julia 中, 函数是一个抽象概念, 一个函数名下可能对应多个具体实现,即方法,比如如下代码函数 f 有 2 个方法:
julia> function f(x::Int64)
x
end
f (generic function with 1 method)
julia> function f(x::String)
"string"
end
f (generic function with 2 methods)运行的时候, 会根据所有参数个数、类型, 选择最 match 的方法执行, 所以叫 Multiple dispatch。 对比一般的 OO 语言, 只是根据 receiver 来决定 dispatch 哪个方法, 所以叫"single dispatch"。
Julia 中 type 也会形成 hierarchy, 如下图: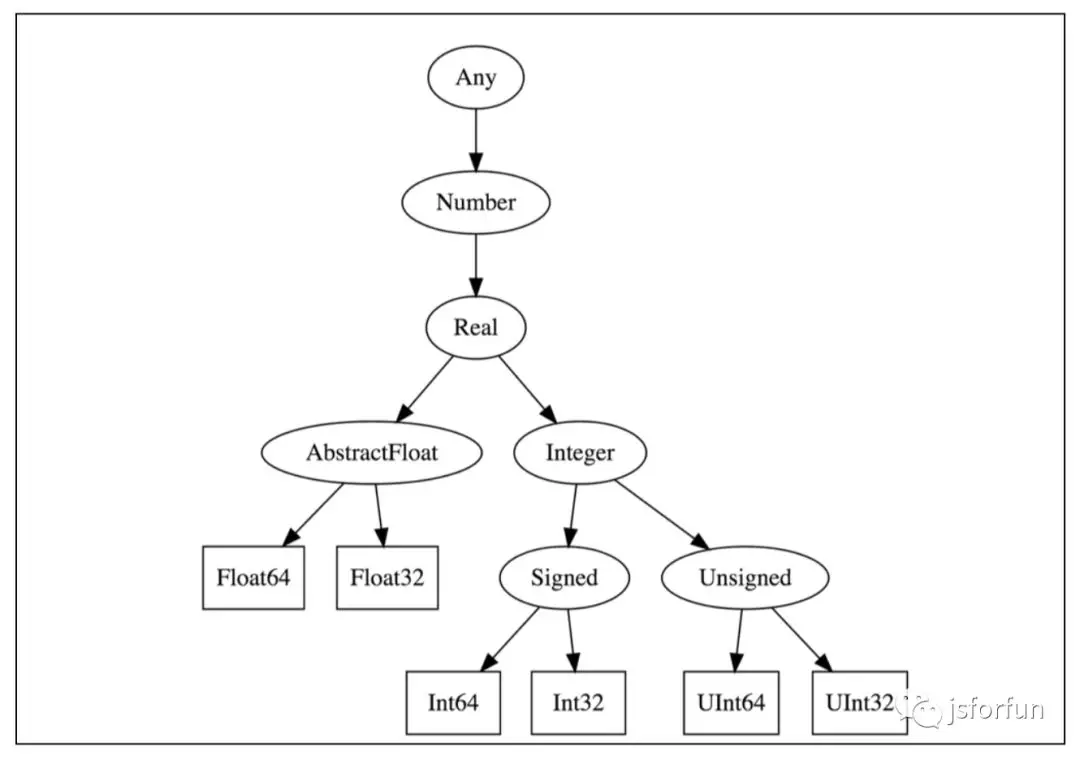
Julia 中,concrete type 不能有 subtypes, 也就是 final 的!
Any是所有的超类, Nothing是所有的子类, Nothing只有一个实例: nothing。
Julia 中的参数类型(类似 Java 的泛型)可以是 value, 比如 Array 的类型为 Array{T, N}, 其中 N 是具体的数字,表示数组的维数:
julia> typeof([1,2])
Array{Int64,1}Julia 的类型推断不是基于著名的 Hindley-Milner 算法(ML 系语言用的类型推断算法, 比如 Scala), 它只会尽力推, 最后在 runtime 如果找不到 match 的方法就会报错。
Type-stability
Type-stability指的是函数返回值类型只取决于参数类型, 而跟参数的具体值无关。 下面的函数就不符合:
function trunc(x)
if x < 0
return 0
else
return x
end
endjulia > trunc(-1.5) |> typeof
Int64
julia > trunc(1.5) |> typeof
Float64|>是 pipeline 操作符, 把前一个操作的结果传入下一个操作, 类似于 linux 的|, 可以方便的将f(g(h(j(x))))改写成可读性更高的x |> j |> h |> g |> f。
要修复trunc的type-stability问题, 可以用 zero 方法:
function trunc_fixed(x)
if x < 0
return zero(x)
else
return x
end
endjulia> -1.5 |> trunc_fixed |> typeof
Float64
julia> 1.5 |> trunc_fixed |> typeof
Float64如果函数是 type-unstable 的话, Julia 编译器没法编译出特定类型的优化的代码, 我们来测试一下:
julia> @benchmark trunc(-2.5)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 0.020 ns (0.00% GC)
median time: 0.030 ns (0.00% GC)
mean time: 0.031 ns (0.00% GC)
maximum time: 8.802 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
julia> @benchmark trunc_fixed(-2.5)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 0.020 ns (0.00% GC)
median time: 0.032 ns (0.00% GC)
mean time: 0.031 ns (0.00% GC)
maximum time: 8.843 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 10001.0 上似乎没有太大区别了,书里的 0.4 版本显示 trunc_fixed 效率是 trunc 的两倍多, 说明 Julia 本身也在不停地改进以及用新版本是很重要的!
如何识别 type-stability 问题呢? Julia 提供了一个@code_warntype宏:
julia> @code_warntype trunc(2.5)
Body::Union{Float64, Int64}
2 1 ─ %1 = π (0.0, Float64) │╻ <
│ %2 = (Base.lt_float)(x, %1)::Bool ││╻ <
│ %3 = π (0.0, Float64) ││
│ %4 = (Base.eq_float)(x, %3)::Bool ││╻ ==
│ %5 = (Base.and_int)(%4, true)::Bool ││╻ &
│ %6 = (Base.and_int)(%5, false)::Bool │││
│ %7 = (Base.or_int)(%2, %6)::Bool ││╻ |
└── goto #3 if not %7 │
3 2 ─ return 0 │
5 3 ─ return x │
julia> @code_warntype trunc_fixed(2.5)
Body::Float64
2 1 ─ %1 = π (0.0, Float64) │╻ <
│ %2 = (Base.lt_float)(x, %1)::Bool ││╻ <
│ %3 = π (0.0, Float64) ││
│ %4 = (Base.eq_float)(x, %3)::Bool ││╻ ==
│ %5 = (Base.and_int)(%4, true)::Bool ││╻ &
│ %6 = (Base.and_int)(%5, false)::Bool │││
│ %7 = (Base.or_int)(%2, %6)::Bool ││╻ |
└── goto #3 if not %7 │
3 2 ─ return 0.0 │
5 3 ─ return x可以看到 trunc 的返回值类型是 Union{Float64, Int64}。 另外也可以用@code_llvm和@code_native两个宏看函数最后生成的 LLVM IR 指令和机器码, 会发现 type-stabe 的函数生成的指令也要少一些。
函数和宏
全局变量的问题
全局变量是 bad smell, 在 Julia 中还会影响性能, 因为全局变量可能在任何时候被修改为任何其他类型, 所以 compiler 没法优化。
julia> p = 2;
julia> function pow_array(x::Vector{Float64})
s = 0.0
for y in x
s = s + y^p
end
return s
end
pow_array (generic function with 1 method)
julia> t = rand(100000);
julia> @benchmark pow_array(t)
BenchmarkTools.Trial:
memory estimate: 4.58 MiB
allocs estimate: 300000
--------------
minimum time: 7.385 ms (0.00% GC)
median time: 8.052 ms (0.00% GC)
mean time: 8.261 ms (2.76% GC)
maximum time: 50.044 ms (85.05% GC)
--------------
samples: 604
evals/sample: 1可以将全局变量修改为const即可:
julia> const p2 = 2
2
julia> function pow_array2(x::Vector{Float64})
s = 0.0
for y in x
s = s + y^p2
end
return s
end
pow_array2 (generic function with 1 method)
julia> @benchmark pow_array2(t)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 81.324 μs (0.00% GC)
median time: 83.629 μs (0.00% GC)
mean time: 87.973 μs (0.00% GC)
maximum time: 185.029 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 1性能差距将近 100 倍!!!内存占用和分配也有很大差别。 用@code_warntype 可以看出两者的差别, pow_array 返回值是 Any 类型, 而 pow_array2 是 Float64 类型, 可见 pow_array2 是 type-stable 的。
Julia 中的 const 可以修改值!但是不能修改类型!
inline
Julia 使用的 LLVM 编译器, 大部分编译优化都是 LLVM 的功劳, 不过 inline 是在 LLVM 之前做的。 Julia 有一套启发式规则, 将“值得 inline”的函数 inline。 inline 会增大 code 的大小,需要权衡。
julia> trunc2(x) = x < 0 ? zero(x) : x
trunc2 (generic function with 1 method)
julia> function sqrt_sin(x)
y = trunc2(x)
return sin(sqrt(y)+1)
end
sqrt_sin (generic function with 1 method)
julia> @code_typed sqrt_sin(-1)
CodeInfo(
2 1 ─ %1 = (Base.slt_int)(x, 0)::Bool │╻╷ trunc2
└── goto #3 if not %1 ││
2 ─ goto #4 ││
3 ─ goto #4 ││
4 ┄ %5 = φ (#2 => 0, #3 => _2)::Int64 │
3 │ %6 = (Base.sitofp)(Float64, %5)::Float64 │╻╷╷╷ sqrt
│ %7 = (Base.lt_float)(%6, 0.0)::Bool ││╻ sqrt
└── goto #6 if not %7 │││
5 ─ invoke Base.Math.throw_complex_domainerror(:sqrt::Symbol, %6::Float64)::Union{} │││
└── $(Expr(:unreachable))::Union{} │││
6 ─ %11 = (Base.Math.sqrt_llvm)(%6)::Float64 │││
└── goto #7 │││
7 ─ goto #8 ││
8 ─ %14 = (Base.add_float)(%11, 1.0)::Float64 ││╻ +
│ %15 = invoke Main.sin(%14::Float64)::Float64 │
└── return %15 │
) => Float64从@code_typed 宏的结果可以看出,并没有调用 trun2,而是直接将 trunc2 的代码 inline 了。 可以用julia --inline=no启动 REPL, 结果会是:
julia> @code_typed sqrt_sin(-1)
CodeInfo(
2 1 ─ %1 = (Main.trunc2)(x)::Int64 │
3 │ %2 = (Main.sqrt)(%1)::Float64 │
│ %3 = (%2 + 1)::Float64 │
│ %4 = (Main.sin)(%3)::Float64 │
└── return %4 │
) => Float64注意, 禁用 inline 会严重影响性能, 只在特殊情况下(比如 debugging 或者 code coverage analysis)才打开。
关掉 inline:
julia> @benchmark sqrt_sin(-1)
BenchmarkTools.Trial:
memory estimate: 1.45 KiB
allocs estimate: 77
--------------
minimum time: 3.114 μs (0.00% GC)
median time: 3.410 μs (0.00% GC)
mean time: 3.749 μs (4.07% GC)
maximum time: 1.232 ms (99.33% GC)
--------------
samples: 10000
evals/sample: 9打开 inline:
julia> @benchmark sqrt_sin(-1)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 8.434 ns (0.00% GC)
median time: 8.682 ns (0.00% GC)
mean time: 9.083 ns (0.00% GC)
maximum time: 35.598 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 999可以看到, 性能差距巨大!
有时候根据 Julia 的默认规则不会 inline, 可以在 function 定义之前手动加上@inline 则可以, 不过最好是经过 profile 之后确定是代码热点才去做。
julia> function f2(x)
a=x*5
a=a*5
d = a
a=a*5
b=a+3
b=b+3
b=b+3
c=a-4
d=b/c
end
f2 (generic function with 1 method)
julia> g(x) = f2(2x)
g (generic function with 1 method)
julia> @code_llvm g(3)
define double @julia_g_35286(i64) {
top:
%1 = mul i64 %0, 250
%2 = add i64 %1, 9
%3 = add i64 %1, -4
%4 = sitofp i64 %2 to double
%5 = sitofp i64 %3 to double
%6 = fdiv double %4, %5
ret double %6
}我们可以看到 LLVM 生成的代码中,第一行是%1 = mul i64 %0, 250, 原因在于 f2 中, a 乘以 3 个 5, 并且 g 的定义中有一个 2 倍, 所以 LLVM 直接优化成了乘以2 * 5 * 5 * 5 = 250。 如果没有 inline 的话,显然是做不到的(5*5*5应该还是可以优化成*125)。
macros
macros 就是在 compile time 用 code 生成 code, 能提前做一些事情, 这样在 runtime 的时候就能少做一些, 性能自然高了。
书中举的例子测试无效, 所以暂时不放了。
named parameters
有时候 function 参数很多, 可以用 named parameters,可以提高代码可读性。 但是性能有点点影响, 大概是 50% 吧。 影响不是太大, 所以建议代码可读性和可维护性优先, 只在 performance-sensitive 的内部循环才不使用。
julia> named_param(x; y=1, z=1) = x^y + x^z
named_param (generic function with 1 method)
julia> pos_param(x,y,z) = x^y + x^z
pos_param (generic function with 1 method)
julia> @benchmark named_param(4, y = 2, z = 3)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 6.535 ns (0.00% GC)
median time: 6.997 ns (0.00% GC)
mean time: 7.228 ns (0.00% GC)
maximum time: 43.993 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
julia> @benchmark pos_param(4, 2, 3)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 4.367 ns (0.00% GC)
median time: 4.500 ns (0.00% GC)
mean time: 4.727 ns (0.00% GC)
maximum time: 38.259 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
欢迎加入知识星球一起分享讨论有趣的技术话题。