上一篇:米田嵌入
原文地址: https://bartoszmilewski.com/2...
如果我还没有使你已经确信范畴论就是所有和态射有关的东西,那就是我的失职。因为下一个主题是伴随,而伴随是用hom集的同构定义的,所以回顾一下有关hom集的那些积木是很有意义的。而且你会看到伴随为描述我们之前研究的很多构造提供了一种更一般的语言,所以复习一下它们也很有必要。
函子
首先,你其实应该把函子看作态射的映射——这个观点有在Haskell的Functor类型类的定义中得到强调,也就是fmap。当然,函子也映射对象——态射的端点——否则我们就没法谈论保持复合。对象告诉了我们哪些态射对是可复合的。其中一个态射的终点必须等于另一个态射的起点——如果它们能复合。所以如果我们想把态射的复合映为提升后的态射的复合,端点的映射就很大程度上被决定了。
交换图
态射的很多性质都是用交换图的方式表达的。如果一个特定的态射被以超过一种方式描述为其他态射的复合,那么我们就有一个交换图了。
特别地,交换图构成了几乎所有泛构造的基础(初始对象和终端对象是明显的例外)。我们已经在积、余积、很多其他(余)极限、指数对象和自由幺半群等等的定义中看到过它了。
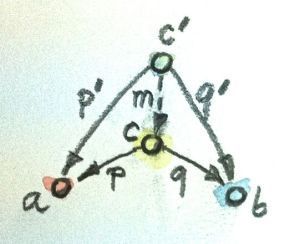
积是泛构造的一个简单例子。我们挑选两个对象a和b,看看是否存在一个带上一对态射p和q的具有成为它们积的泛性质的对象c。
积是极限的一个具体例子。极限是用锥的观念定义的。泛锥是构建在交换图之上的。这些图表的交换性可以被一个恰当的函子的映射的自然性条件所代替。这种方式下交换性被降为了汇编语言的角色,而高级语言是自然变换。
自然变换
一般来说,当我们需要从态射映为交换四方图的时候,自然变换会非常方便。自然四方图的两个对边是某个态射f在两个函子F和G作用下的像。另外的边则是自然变换的分量(当然这也是态射)。
自然性意味着当你移动到“相邻”分量(相邻的意思是说由一个态射连接)上时,你不会违背范畴的结构,也不会违背这两个函子的。你是先用自然变换的分量桥接对象,再用函子跳到它的邻居上;还是反过来,这一点关系也没有。这两个方向是正交的。自然变换让你左右移动,函子让你上下活着前后移动——打个比方说。你可以设想一个函子的像就是靶范畴里的一页纸。自然变换就把对应于F的这样一页纸映为对应G的另一页。
我们已经见过Haskell中这个正交性的例子了。在Haskell中函子在不改变容器形状的条件下修改了容器的内容,而自然变换把这些内在的内容重新打包到另一个不同的容器中。这些操作的顺序并不重要。
我们已经在极限的定义中见到过用自然变换表示的锥了。自然性确保了每个锥的边是可交换的。然而,极限使用锥之间的映射定义的。这些映射也必须满足交换性条件(比如,积的定义中的三角形必须交换。)
这些条件也可以被自然性所代替。你可能会想起泛锥,或者说极限,被定义成一个自然变换,这个自然变换是(逆变)hom函子:
F :: c -> C(c, Lim D)和把C的对象映为锥的(逆变)函子(当然锥本身就是自然变换):
G :: c -> Nat(Δ_c, D)之间的。这里,Δ_c是常函子,而D是定义了C中的图表的那个函子。函子F和G都在C的态射上定义良好。非常碰巧的是这个F和G之间特别的自然变换是一个同构。
自然同构
自然同构——每个分量都是可逆的自然变换——是范畴论里描述"两个东西一样"的方法。这样的一个变换的分量必须是对象间的同构——可逆的态射。如果你把函子的像想成纸张,自然同构就是一个这些纸张间的一一可逆映射。
Hom集
但什么是态射呢?它们比对象具有更多的结构:不像对象那样,态射有两个端。如果你固定住源对象和靶对象,这两个对象间的态射就构成了一个无聊的集合(至少对于局部小的范畴来说)。我们可以给这个集合的元素一些像f和g这样的名字来区分它们——但究竟是什么让它们区别于彼此?
在一个给定的hom集上,态射间的本质区别表现在它们与其他态射(来自相邻的hom集)的复合上。如果有一个态射h,它与f的复合(前复合或后复合)与g不同,例如:
h ∘ f ≠ h ∘ g这样我们就能够直接“观察”f和g的不同。然而就算这个区别不能直接观察,我们也可以使用函子去放大hom集。函子F可以把这两个态射映为不同的态射:
F f ≠ F g在更富的范畴里,相邻的hom集会提供更高的分辨率,比如,
h' ∘ F f ≠ h' ∘ F g其中h'不在F的像里。
Hom集同构
很多范畴论的构造依赖于hom集间的同构。但因为hom集仅仅只是集合,它们之间一般的同构并不会告诉你更多的东西。对于有限集,同构只是说他们有相同多的元素。如果集合是无限的,它们的基数必须是相同的。但是,任意有意义的hom集同构必须考虑复合。而复合涉及了不止一个hom集。我们需要定义跨在所有hom集的集族上的同构,我们还需要对涉及复合的操作加以某些兼容性条件。而自然同构精确地满足了这样的要求。
但什么是hom集的自然同构呢?自然性是一个函子间的映射的性质,并不是集合间的。所以我们真正在谈论的是指向hom集的函子间的自然同构。它们在态射上的行为由恰当的hom函子导出。态射标准地被hom函子用前复合或后复合(取决于函子的协变性)的方式映射。
米田嵌入就是这种同构的一个例子。它把C中的hom集映为函子范畴里的hom集;并且它是自然的。米田嵌入中的一个函子是C中的hom函子,另一个把对象映为hom集间的自然变换的集合。
极限的定义也是hom集间的一个自然同构(第二个hom集,同样,也是函子范畴里的):
C(c, Lim D) ≃ Nat(Δ_c, D)可以证明我们的指数对象的构造,或者自由幺半群的构造,也能被重写成hom集上的自然同构。
这并非巧合——我们接下来将会看到这些只不过是伴随的不同的例子,而伴随就是用hom集间的自然同构定义的。
hom集的反对称性
还有一种观察可以帮助我们理解伴随。hom集,一般来说,是非对称的。hom集C(a, b)通常与hom集C(b, a)非常地不一样。这种非对称性的极端例子就是看成范畴的偏序。在偏序中,从a到b的态射存在当且仅当a小于等于b。如果a和b不相等,那么另一个方向,也就是b到a就不会有态射。所以如果hom集C(a, b)非空,这就意味着它是个单例集,那么C(b, a)必须是空集,除非a = b。在这个范畴中箭头有一个明确的流向。
而没有反对称性的预序,也是“几乎全部”有向的,除了例外的环形。把任意的范畴看成预序的推广是非常方便的方法。
预序是个薄范畴——所有的hom集或者是单例集或者是空集。我们可以把一般的范畴看成一个“厚的”预序。
挑战
- 考虑某些自然性条件的退化情况并画图。例如,如果函子
F或G把对象a和b(f :: a -> b的端)映为同一个对象,比如,F a = F b或G a = G b?(注意你会得到一个锥或者余锥。)然后考虑F a = G a或F b = G b的情况。最后,如果从一个指向自己的环态射——f :: a -> a开始呢?
致谢
感谢Gershom Bazerman检查我的数学和逻辑,以及André van Meulebrouck在整个系列中的编辑上的帮助。
下一篇:伴随