HashSet
elem1,elem2,elem3...如果这一系列元素放到
- 数组;查找O(n),插入O(n),删除O(n)
- 链表;查找o(n),插入o(1),删除o(1)
- HashSet;查找o(1),插入o(1),删除o(1)
HashSet的实现原理
HashSet是通过数组查找复杂度为0(1)实现的.
数组[hashfunction(elem)] = elem 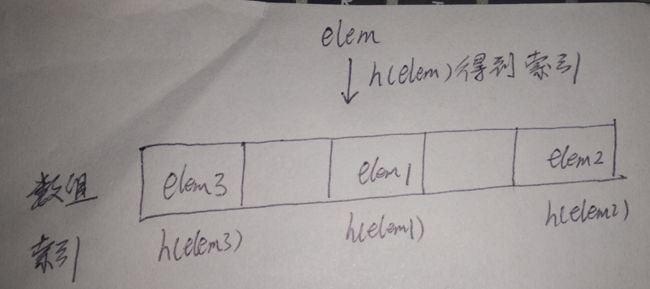
完全一致散列
每个key生成的数组索引都是唯一的,且所有key生成的数组索引互不相同.
非完全一致散列
每个key生成的数组索引都是唯一的,但是存在多个key生成的数组索是相同的情况.
这时,就有了冲突,填充因子,重构哈希表等概念了.
[针对完全一致散列的散列表的查找,插入,删除过程]
利用元素进行哈希函数运算得到数组的索引,然后把该元素放置到数组的索引单元中.
查找时,进行哈希计算迅速得到元素的位置,如果该位置是null,表明无此元素;
插入时,经过哈希运算,找到存储位置,检查存储位置如果为null,则插入;如果不是null,表明已经存在,则出错;所以将元素插入时,建议插入前先检查是否已经存在待插入的元素.
删除时同理,置为null即可.
散列表
散列表,又称字典,关联数组。
一系列key-value形式的元素存放到某种数据结构中,能通过key迅速找到该数据对,如
电话薄中的手机号码,[姓名,号码]
(张三,18700977521)
(李四,15810387653)
(王二,13190008765)
实现方案
我们先根据key生成key的hashset(数组a),然后额外创建一个数组b,数组b和数组a长度相同;假设key1在数组a中的索引是h(key1),那么我们就在数组b的h(key1)索引单元放置key1对应的value1.
当我们查找某个key的value时,通过h(key)得到其value在数组b中的索引.
当我们判断散列表是否已经包含key-value对时,取得key的hashset数组a,即可0(1)时间内实现判断.
切记,数组a和数组b称为关联数组,数组a是hashset,但是存放value的数组b并不是hashset,它只是哥普通数组.
散列表的应用案例
- 手机的联系人列表,能快速定位到某个朋友的手机号码.
- 去重.将一堆元素逐个扔进散列表,重复的就丢弃,时间复杂度是o(n)
- 缓存.某一Twitter用户对服务器发出请求,服务器计算得到相应的界面,发送给用户;对于登陆,注册等界面,所有的用户都是相同的,我们可以把这些固定不变的界面缓存下来,放入到一个字典中.
HashTable的瓶颈
碰撞
多个key经过哈希函数的计算得到的数组索引值相同,称为碰撞.
解决碰撞的办法有:(1)链接法 (2)开放地址法
装载因子
装载因子 = 散列表的元素数目 / 数组长度
当装载因子 达到0.7时,建议延长散列表的长度,不至于使数组每个单元链接的元素数目太长,降低了散列表的性能.
证明哈希表的时间复杂度是O(1)
假设n个元素,数组长度是m,哈希函数具有良好的随机性,那么我们查找某个元素的时间复杂度是O(n/m),同时我们会在填充因子大于0.7时扩充数组的长度,即,n和m是线性关系,m = kn(k是常数),所以有 O(n/m) = O(n / kn) = O(1/k) = O(1).
HashTable的最坏情况
HashTable允许出现碰撞,但是如果采用的哈希函数极其恶心,把很多key都链接到数组的相同索引,这时候查找的时间复杂度是O(n).
一个好的哈希函数是HashTable的命,直接决定散列表的性能.
一个好的哈希函数应该让每个key独立且随机的生成索引,从而尽可能的逼近这样的一种状态:数组的绝大部分单元都链接了元素,且每个单元链接的元素数目大致相等.
最佳状态称为完全一致散列,即数组的每个单元都存放一个元素!

