Hash查找
Hash查找
- 引入:
- 一些认识:
- Hash函数
- 解决冲突
引入:
我们知道,数组的最大特点就是:寻址容易,插入和删除困难;而链表正好相反,寻址困难,而插入和删除操作容易。那么如果能够结合两者的优点,做出一种寻址、插入和删除操作同样快速容易的数据结构。这就是哈希表创建的基本思想,哈希表就是这样一个集查找、插入和删除操作于一身的数据结构。
哈希表(Hash Table):也叫散列表,是根据关键码值(Key-Value)而直接进行访问的数据结构,也就是我们常用到的map。
哈希函数:也称散列函数,是Hash表的映射函数,它可以把查找表中的关键字映射成该关键字对应的地址函数,表示如下:
Hash(key)=Addr,(地址可以是数组下标、索引、内存地址等)
哈希函数能使对一个数据序列的访问过程变得更加迅速有效,通过哈希函数数据元素能够被很快的进行定位。
哈希函数的规则是:通过某种转换关系,使关键字适度的分散到指定大小的的顺序结构中,越分散,则以后查找的时间复杂度越小,空间复杂度越高。
冲突:两个不同的关键字,由于散列函数值相同,因而被映射到同一表位置上。该现象称为冲突(Collision)或碰撞
一些认识:
查找复杂度:对于无冲突的Hash表而言,查找复杂度为O(1)(注意,在查找之前我们需要构建相应的Hash表)。
我们在实际编程中存储一个大规模的数据,最先想到的存储结构可能就是map。map的本质就是Hash表。
Hash是一种典型以空间换时间的算法,比如原来一个长度为100的数组,对其查找,只需要遍历且匹配相应记录即可,从空间复杂度上来看,假如数组存储的是byte类型数据,那么该数组占用100byte空间。现在我们采用Hash算法,我们前面说的Hash必须有一个规则,约束键与存储位置的关系,那么就需要一个固定长度的hash表,此时,仍然是100byte的数组,假设我们需要的100byte用来记录键与位置的关系,那么总的空间为200byte,而且用于记录规则的表大小会根据规则,大小可能是不定的。
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
Hash函数
正整数
获取正整数哈希值最常用的方法是使用除留余数法。即对于大小为素数M的数组,对于任意正整数k,计算k除以M的余数。M一般取素数。
字符串
将字符串作为键的时候,我们也可以将他作为一个大的整数,采用保留除余法。我们可以将组成字符串的每一个字符取值然后进行哈希,比如
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
for (int i = 0; i < s.Length; i++)
{
hash = s[i] + (31 * hash);
}
return hash;
}
上面的哈希值是Horner计算字符串哈希值的方法,公式为:
如果对每个字符去哈希值可能会比较耗时,所以可以通过间隔取N个字符来获取哈西值来节省时间,比如,可以 获取每8-9个字符来获取哈希值:
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
int skip = Math.Max(1, s.Length / 8);
for (int i = 0; i < s.Length; i+=skip)
{
hash = s[i] + (31 * hash);
}
return hash;
}
总结:
直接定址法:直接取关键字的某个线性函数值作为散列地址,例如:
H(key)=a×key+b,(a和b均为常数)H(key)=a×key+b,(a和b均为常数) H(key) = a \times key + b,(a和b均为常数)H(key)=a×key+b,(a和b均为常数)
适合关键字分布基本连续的情况,否则容易造成存储空间浪费。
除留余数法:(最常用) 假定表长为m,取一个不大于m但最接近或者等于m的质数P,例如:
H(key)=key%PH(key)=key%P H(key) = key%PH(key)=key%P
数字分析法:比如有一组value1=112233,value2=112633,value3=119033,针对这样的数我们分析数中间两个数比较波动,其他数不变。那么我们取key的值就可以是key1=22,key2=26,key3=90。
适合于已知关键字的集合分布,关键字位数较大的情况。
平方取中法:取关键字的平法值的中间几位作为散列地址。
适合于不是道关键字分布,且关键字每一位取值不均匀或均小于散列地址所需的位数。
折叠法:举个例子,比如value=135790,要求key是2位数的散列值。那么我们将value变为13+57+90=1601,然后去掉高位“1”,此时key=60,这就是他们的哈希关系。这样做的目的就是key与每一位value都相关,来达到“散列地址”尽可能分散的目的。适合于不需要知道关键字分布,关键字位数较多的情况。
解决冲突
拉链法:
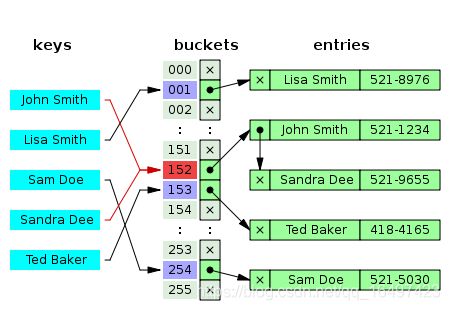
图中,”John Smith”和”Sandra Dee” 通过哈希函数都指向了152 这个索引,该索引又指向了一个链表, 在链表中依次存储了这两个字符串。
该方法的基本思想就是选择足够大的M,使得所有的链表都尽可能的短小,以保证查找的效率。对采用拉链法的哈希实现的查找分为两步,首先是根据散列值找到等一应的链表,然后沿着链表顺序找到相应的键。
首先我们需要定义一个链表的总数,在内部我们定义一个SequentSearchSymbolTable的数组。然后每一个映射到索引的地方保存一个这样的数组。
public class SeperateChainingHashSet<TKey, TValue> : SymbolTables<TKey, TValue> where TKey : IComparable<TKey>, IEquatable<TKey>
{
private int M;//散列表大小
private SequentSearchSymbolTable<TKey, TValue>[] st;//
public SeperateChainingHashSet()
: this(997)
{
}
public SeperateChainingHashSet(int m)
{
this.M = m;
st = new SequentSearchSymbolTable<TKey, TValue>[m];
for (int i = 0; i < m; i++)
{
st[i] = new SequentSearchSymbolTable<TKey, TValue>();
}
}
private int hash(TKey key)
{
return (key.GetHashCode() & 0x7fffffff) % M;
}
public override TValue Get(TKey key)
{
return st[hash(key)].Get(key);
}
public override void Put(TKey key, TValue value)
{
st[hash(key)].Put(key, value);
}
}
可以看到,该实现中使用
Get方法来获取指定key的Value值,我们首先通过hash方法来找到key对应的索引值,即找到SequentSearchSymbolTable数组中存储该元素的查找表,然后调用查找表的Get方法,根据key找到对应的Value。
Put方法用来存储键值对,首先通过hash方法找到改key对应的哈希值,然后找到SequentSearchSymbolTable数组中存储该元素的查找表,然后调用查找表的Put方法,将键值对存储起来。
hash方法来计算key的哈希值, 这里首先通过取与&操作,将符号位去除,然后采用除留余数法将key应到到0-M-1的范围,这也是我们的查找表数组索引的范围。
实现基于拉链表的散列表,目标是选择适当的数组大小M,使得既不会因为空链表而浪费内存空间,也不会因为链表太而在查找上浪费太多时间。拉链表的优点在于,这种数组大小M的选择不是关键性的,如果存入的键多于预期,那么查找的时间只会比选择更大的数组稍长,另外,我们也可以使用更高效的结构来代替链表存储。如果存入的键少于预期,索然有些浪费空间,但是查找速度就会很快。所以当内存不紧张时,我们可以选择足够大的M,可以使得查找时间变为常数,如果内存紧张时,选择尽量大的M仍能够将性能提高M倍。
线性探测法是开放寻址法解决哈希冲突的一种方法,基本原理为,使用大小为M的数组来保存N个键值对,其中M>N,我们需要使用数组中的空位解决碰撞冲突。
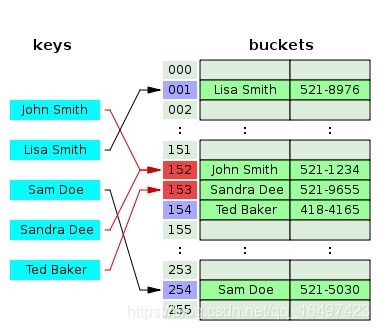
对照前面的拉链法,在该图中,”Ted Baker” 是有唯一的哈希值153的,但是由于153被”Sandra Dee”占用了。而原先”Snadra Dee”和”John Smith”的哈希值都是152的,但是在对”Sandra Dee”进行哈希的时候发现152已经被占用了,所以往下找发现153没有被占用,所以存放在153上,然后”Ted Baker”哈希到153上,发现已经被占用了,所以往下找,发现154没有被占用,所以值存到了154上。
开放寻址法中最简单的是线性探测法:当碰撞发生时即一个键的散列值被另外一个键占用时,直接检查散列表中的下一个位置即将索引值加1,这样的线性探测会出现三种结果:
命中,该位置的键和被查找的键相同
未命中,键为空
继续查找,该位置和键被查找的键不同。
实现线性探测法也很简单,我们只需要两个大小相同的数组分别记录key和value。
public class LinearProbingHashSet<TKey, TValue> : SymbolTables<TKey, TValue> where TKey : IComparable<TKey>, IEquatable<TKey>
{
private int N;//符号表中键值对的总数
private int M = 16;//线性探测表的大小
private TKey[] keys;
private TValue[] values;
public LinearProbingHashSet()
{
keys = new TKey[M];
values = new TValue[M];
}
private int hash(TKey key)
{
return (key.GetHashCode() & 0xFFFFFFF) % M;
}
public override TValue Get(TKey key)
{
for (int i = hash(key); keys[i] != null; i = (i + 1) % M)
{
if (key.Equals(keys[i])) { return values[i]; }
}
return default(TValue);
}
public override void Put(TKey key, TValue value)
{
int hashCode = hash(key);
for (int i = hashCode; keys[i] != null; i = (i + 1) % M)
{
if (keys[i].Equals(key))//如果和已有的key相等,则用新值覆盖
{
values[i] = value;
return;
}
//插入
keys[i] = key;
values[i] = value;
}
}
}
线性探查(Linear Probing)方式虽然简单,但是有一些问题,它会导致同类哈希的聚集。在存入的时候存在冲突,在查找的时候冲突依然存在。
不管是拉链法还是散列法,这种动态调整链表或者数组的大小以提高查询效率的同时,还应该考虑动态改变链表或者数组大小的成本。散列表长度加倍的插入需要进行大量的探测, 这种均摊成本在很多时候需要考虑。
哈希碰撞攻击:
我们知道如果哈希函数选择不当会使得大量的键都会映射到相同的索引上,不管是采用拉链法还是开放寻址法解决冲突,在后面查找的时候都需要进行多次探测或者查找, 在很多时候会使得哈希表的查找效率退化,而不再是常数时间。下图清楚的描述了退化后的哈希表:
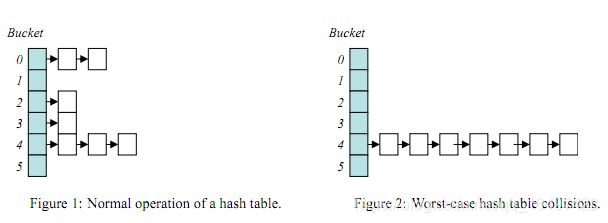
哈希表攻击就是通过精心构造哈希函数,使得所有的键经过哈希函数后都映射到同一个或者几个索引上,将哈希表退化为了一个单链表,这样哈希表的各种操作,比如插入,查找都从O(1)退化到了链表的查找操作,这样就会消耗大量的CPU资源,导致系统无法响应,从而达到拒绝服务供给(Denial of Service, Dos)的目的。
public override unsafe int GetHashCode()
{
if (HashHelpers.s_UseRandomizedStringHashing)
{
return InternalMarvin32HashString(this, this.Length, 0L);
}
fixed (char* str = ((char*) this))
{
char* chPtr = str;
int num = 0x15051505;
int num2 = num;
int* numPtr = (int*) chPtr;
int length = this.Length;
while (length > 2)
{
num = (((num << 5) + num) + (num >> 0x1b)) ^ numPtr[0];
num2 = (((num2 << 5) + num2) + (num2 >> 0x1b)) ^ numPtr[1];
numPtr += 2;
length -= 4;
}
if (length > 0)
{
num = (((num << 5) + num) + (num >> 0x1b)) ^ numPtr[0];
}
return (num + (num2 * 0x5d588b65));
}
}
参考理解
