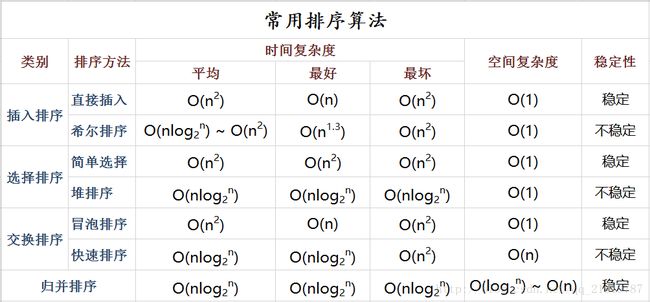
7种排序算法的Python实现
概述
使序列成为一个按关键字有序的序列
稳定性:排序前 ki=kj(1<=i,j<=n,i!=j) && ij 排序方法不稳定
内排序:待排序的所有记录全部被放置在内存中。
外排序:整个排序过程需要在内外存之间多次交换数据。
直接插入
"""直接插入排序
思想
将一个记录插入到有序的序列中
时间复杂度
平均 o(n^2)
最好 o(n), 比较n-1次
最坏 o(n^2), 比较2+3+...+n次,交换3+4+...+n+1次
"""
array = [44, 32, 24, 23, 21, 18, 15, 10, 4, 2]
length = len(array)
def straight_insertion_sort():
for i in range(2, length):
if array[i] < array[i-1]:
temp = array[i] # 设置哨兵
j = i-1
while temp < array[j] and j >= 0:
array[j], array[j+1] = array[j+1], array[j]
j -= 1
array[j+1] = temp
straight_insertion_sort()
print(array)希尔排序
"""希尔排序
插入排序的改进版
思想
将相聚某个“增量”(increment)的记录组成一个子序列,各子序列分别进行插入排序以使子序列基本有序。
基本有序:小的关键字基本在前,大的关键字基本在后,不大不小的关键字基本在中间。
增量序列的最后一个增量值必须为1,增量公式int(increment / 3 + 1)。
时间复杂度
"""
array = [44, 32, 24, 23, 21, 18, 15, 10, 4, 2]
length = len(array)
def shell_sort():
increment = length
while increment > 1:
increment = int(increment / 3 + 1) # 增量公式
for i in range(increment, length, increment):
if array[i] < array[i-increment]:
temp = array[i]
j = i - increment
while temp < array[j] and j >= 0:
array[j], array[j + increment] = array[j + increment], array[j]
j -= increment
array[j + increment] = temp
shell_sort()
print(array)简单选择
"""简单选择排序
思想
通过n-i次关键字比较,在n-i+1个元素中选出关键字最小(大)的记录,并和第i个记录交换。
时间复杂度
平均 o(n^2)
最好 o(n^2),比较n-1次
最坏 o(n^2),比较n-1+n-2+...+1=n(n-1)/2次,交换n-1次
"""
array = [44, 32, 24, 23, 21, 18, 15, 10, 4, 2]
length = len(array)
def simple_selection_sort():
for i in range(0, length-1):
min = i
for j in range(i+1, length):
if array[min] > array[j]:
min = j
if min is not i:
array[min], array[i] = array[i], array[min]
simple_selection_sort()
print(array) 堆排序
"""堆排序
思想
1.将待排序序列构建成一个大(小)顶堆,此时整个序列的最大(小)值就是堆顶的根节点。
2.将大(小)顶堆根节点与堆数组的末尾元素交换
3.然后将除末尾以外的元素重新构造成一个大(小)顶堆
4.如果堆的节点个数大于1,回到2
堆是一个完全二叉树
大顶堆:每个节点的值都大于或等于其左右孩子节点的值
小顶堆:每个节点的值都小于或等于其左右孩子节点的值
"""
# 注意:这是完全二叉树,为方便运算(堆第i个节点的左孩子节点和右孩子节点位置分别是2i, 2i+1,),第一个元素一定要放在下标为1的位置
array = [0, 50, 10, 90, 30, 70, 40, 80, 60, 20]
length = len(array)-1
def heap_sort():
# 构建堆
for i in range(int(length/2), 0, -1):
adjust(i, length)
# 调整剩余元素为一个新的堆
for i in range(length, 1, -1):
array[1], array[i] = array[i], array[1]
adjust(1, i-1)
def adjust(p, length):
temp = array[p]
i = 2*p
while i <= length:
if i+1 <= length and array[i] < array[i+1]:
i += 1
if temp > array[i]:
break
array[p] = array[i]
p = i
i *= 2
array[p] = temp
heap_sort()
print(array)冒泡排序
"""冒泡排序
思想
两两比较相邻记录
时间复杂度
平均 o(n^2)
最好 o(n) 本身有序,比较n-1次
最坏 o(n^2) 本身逆序,比较1+2+3+...+(n-1)=n(n-1)/2次,交换1+2+3+...+(n-1)=n(n-1)/2次
"""
array = [44, 32, 24, 23, 21, 18, 15, 10, 4, 2]
length = len(array)
def bubble_sort_1():
"""
从后往前比较
"""
i = 0
while i < length-1:
j = length-2
while j >= i:
if array[j] > array[j+1]:
array[j], array[j + 1] = array[j + 1], array[j] # python中交换简写
j -= 1
i += 1
def bubble_sort_2():
"""
从前往后比较
"""
i = 0
while i < length-1:
j = 0
while j < length-1-i:
if array[j] > array[j+1]:
array[j], array[j + 1] = array[j + 1], array[j] # python中交换简写
j += 1
i += 1
def bubble_sort_improved():
"""冒泡排序改进版
当序列近似顺序时,避免不必要的比较,提高效率
"""
i = 0
flag = True
while i < length-1 and flag: # 当flag为False,退出循环
flag = False
j = length-2
while j >= i:
if array[j] > array[j+1]:
array[j], array![j+1] = array[j+1],array[j]
flag = True
j -= 1
i += 1
bubble_sort_2()
print(array)快速排序
"""快速排序
思想
1.选取序列中一个元素作为枢轴,让其左边的值都比它小,右边的值都比它大。
2.将序列以枢轴为界限分割为左右两部分序列,如果分割后的序列的元素个数大于1,则执行步骤1。
"""
array = [32, 50, 10, 30, 30, 70, 40, 80, 60, 20]
length = len(array)
def quick_sort(f, r):
if f >= r:
return
i = f
j = r
temp = array[f]
while f < r:
while f < r and temp <= array[r]: # 从后向前比较
r -= 1
if f < r:
array[f] = array[r]
while f < r and temp >= array[f]: # 从前向后比较
f += 1
if f < r:
array[r] = array[f]
array[r] = temp # 此时r和j重合
quick_sort(i, f-1)
quick_sort(f+1, j)
quick_sort(0, 9)
print(array)归并排序
"""归并排序
思想
序列含有n个记录,可以看成n个有序子序列,每个子序列的长度为1,然后两两归并。
"""
array = [32, 50, 10, 30, 30, 70, 40, 80, 60, 20]
length = len(array)
def merging_sort(f, r):
if f >= r:
return
mid = int((f+r)/2)
merging_sort(f, mid)
merging_sort(mid+1, r)
merge(f, mid, r)
def merge(f, mid, r):
temp = []
i = f
j = mid+1
while i <= mid and j <= r:
if array[i] <= array[j]:
temp.append(array[i])
i += 1
else:
temp.append(array[j])
j += 1
while i <= mid:
temp.append(array[i])
i += 1
while j <= r:
temp.append(array[j])
j += 1
for k in range (0, len(temp)):
array[f+k] = temp[k]
merging_sort(0, 9)
print(array)