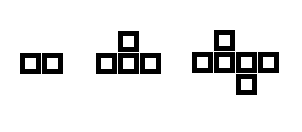算法设计与分析基础 第四章谜题

习题4.1

1.摆渡的士兵 n个士兵组成的分队必须越过一条又深又宽又没有桥的河。他们注意到在岸旁有两个12岁大的小男孩在玩划艇。然而船非常小，只能容纳两个男孩或一名士兵。怎样才能让士兵渡过河，并且留下两个男孩操纵这条船？这条船要在岸与岸之间横渡多少次？

解答：每次只能容纳一名士兵，所以士兵一定是一个一个过河，同时需要有小男孩将船划回来，那么每一次士兵过河之前，两个小男孩先划船过去，然后一个小男孩划船回来，另一个小男孩在士兵过河之后把船划回来。所以摆渡n个士兵，需要执行这样的步骤n次，每次船在岸与岸之间横渡4次，共4n次。

 

2.交替放置的玻璃杯 有2n个玻璃杯挨个排成一行，前n个装满苏打水，其余n个杯子为空。交换杯子的位置，使之按照一空一满一空(filled-empty-filledempty pattern，翻译有误)的模式排列，而且杯子的移动次数最少。

解答：给2n个杯子从左至右从1开始依次编号，将第2个杯子与第n-1个杯子互换，那么此问题转化为2(n-2)个杯子的问题。交换次数M(n)=M(n-2)+1,当n>2时; M(1)=0;M(2)=1.

 

3.标记单元格 为下列任务设计一个算法。n为任意偶数，在一张无限大的绘图个字纸上标记n个单元格，使得每个被标记的单元格有奇数个相邻的标记单元格。相邻是指两个单元格在水平方向两个单元格在水平方向或垂直方向上相邻，但非对角方向上相邻。被标记的单元格必须形成连续域，也就是说区域中任意一对标记单元格之间有一条经过一系列相邻标记单元格的路径。

解答：根据题意，以下列出了n=2,4,6的标记结果，每增加两个标记格，则只能在水平方向（该方向可任意指定）增加一个单元格，在竖直方向交替增加一个单元格，只有这样才能满足题目要求。

6.队伍排序 给定一个完全循环赛的比赛结果，其中n个队伍两两比赛一次。每场比赛以一方胜出或者平局结束。设计一个算法，把n个队伍排序，序列中每个队伍都不曾输给紧随其后的那个队。说明该算法的时间效率类型。

解答：以任意一个队伍初始化所求序列，然后将其他队伍依次插入该序列。插入过程中，将当前队伍与序列中的队伍从前到后一一比较，若找到胜利或者平局的队伍，则插入到该队伍的前方，否则会一直比较，直到最后插入队伍末端。该算法的效率类型为O(n2)，最差情况下每次插入时都位于队伍最末端。

 

习题4.2

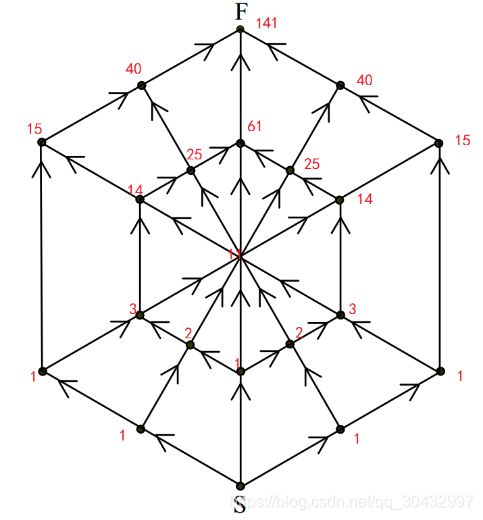
10.蛛网问题 一只蜘蛛位于网的底端(S)，而一只苍蝇位于网的顶端(F)。沿着箭头方向在线上移动，蜘蛛有多少不同的路径到达苍蝇处？

解答：从S出发按照拓扑排序的顺序依次遍历节点，对每个节点计算从S出发到达它存在多少路径，计算方法是对所有前驱节点的路径数求和。计算得到到达F节点的路径数是141。

习题4.3

11.格雷码和汉诺塔

a. 为什么汉诺塔的经典递归算法产生的移动盘子动作可以用来生成二进制反射格雷码？

解答：题目原文：Show that the disk moves made in the classic recursive algorithm for the Tower-of-Hanoi puzzle can be used for generating the binary reflected Gray code.

定义从小到大的盘子序号分别为1，2，……n，初始化一个全为0的n位序列，m号盘子对应从右到左的第m位，每次移动一个盘子，则该位的元素翻转，构成二进制反射格雷码的一个序列。

b. 如何利用二进制反射格雷码来解决汉诺塔问题？

解答：在生成格雷码的算法中，依次改变的位数是最低位和从右往左数第一个1所在位的左一位，对应汉诺塔的盘子就是最小的盘子和中间某个盘子。最小的盘子有两种可能的移动方案，其他的盘子只有一种可能。对于最小盘子移动到的柱子的解决方法是，根据观察，当盘子总数是奇数时，最小盘子的位置依次是“3->2->1->3->2->1...”；当总数是偶数时，这个顺序是“2->3->1->2->3->1...”。据此从格雷码到汉诺塔的一种对应解决方案就产生了。

 

12.展会彩灯 早些年，在展会上可能会看到这样一种彩灯：一个被连接到若干开关上的电灯泡，只当所有开关闭合的时候才会发光。每一个开关由一个按钮控制；按下按钮就会切换开关状态，但是开关的状态是无法知道的。目标就是点亮灯泡。设计一个点亮灯泡的算法，使其在有你n个开关时，在最坏的情况下，需要按动按钮的次数最少。

解答：可以利用二进制反射格雷码的特性，相邻两个位串只相差一位数字，而2n个位串都是不同的。将n个开关分别对应n位二进制格雷码的每一位，每当格雷码的序列某一位发生变化，切换对应的开关状态。

 

习题4.4

7.猜图片 一个非常流行的解题游戏是这样的：给选手出示42张图片，每行6张，共7行。选手可以给大家做一些是非题，来确定他要寻找的图片。然后进一步要求选手用尽可能少的问题来确定目标图片。给出解决问题的最有效的算法，并指出需要提问的最大次数。

解答：把42张图片依次标号，用二分查找方法，比如第一个问题是“目标图片的序号是不是大于21？”，所需提问的最大次数是

 

10.a.为假币问题的三分算法写一段伪代码。请确保该算法会正确处理所有的n值，而不仅仅是那些3的倍数。

解答： 每次平均分三堆的结果可能有：余数0、余数1、余数2

如果余数0：平均分，任选两堆（堆1+堆2）比较，如果平衡：堆3含假币；如果不平衡：比较堆1和堆3，如果平衡：堆2含假币；如果不平衡：堆1含假币；

余数1:平均分后得到3堆+1个硬币，任选两堆（堆1+堆2）比较，如果平衡：比较堆1和堆3，如果平衡：剩余的单个硬币为假，如果不平衡：堆3为含假币的堆;如果不平衡：比较堆1和堆3，如果平衡：堆2含假币；如果不平衡：堆1含假币

余数2:平均分后得到3堆+2个硬币，任选两堆（堆1+堆2）比较，如果平衡：比较堆1和堆3，如果平衡：假币在两个单个硬币中，这两个硬币必然是不平衡的，这时从堆中找出任意一枚硬币，从两个单个硬币中拿出硬币1进行比较，如果平衡：假币为币2；如果不平衡，假币为币1；如果堆1和堆3不平衡：堆3为含假币的堆，如果不平衡：比较堆1和堆3，如果平衡：堆2含假币；如果不平衡：堆1含假币。

b.为假币问题的三分算法的称重次数建立一个递推关系，并在n=3^k的情况下对它求解。

解答：称重次数W(n)=W( )+1,当n>1;W(1)=0。当n=3^k，W(3^k)=W(3^k-1)+1，解得W(3^k)=k=log3n。

c.当n的值非常大时，该算法要比把硬币分成两堆的算法快多少倍？这个答案应该与n无关。

解答：

 

习题4.5

10.另类单堆拈游戏 请考虑这个另类的单堆拈游戏，它规定谁拿走最后一个棋子就输了。该游戏的其他条件都不变，即该堆棋子有n个，每次每个玩家最多拿走m个，最少拿走1个棋子。请指出该游戏的胜局和败局是怎样的？

分析：当n=1，先拿的人输；当2<=n<=m+1,先拿的人选择n-1个棋子拿走能够赢；当n=m+2，先拿的人会输……以此类推。

解答：败局是n mod (m+1) = 1，胜利的策略是每次拿走(n-1) mod (m+1)的棋子。

 

11.坏巧克力 两个玩家轮流掰一块m×n格的巧克力，其中一块1×1的小块是坏的。每次掰只能顺着方格的边界，沿直线一掰到底，每掰一次，掰的人把两块中不含坏巧克力的那块吃掉，谁碰到最后那块块巧克力就算输了。在这个游戏中，先走好还是后走好？

解答：相当于多堆拈游戏，每边到达坏巧克力块的距离就是一堆，然后用二进制数位和计算。

 

写一个互动程序，让大家可以和这个计算机玩这个游戏。这个程序在胜局应该走出致胜一步，在败局中则只要随机下出合理的一步即可。

#include  
//巧克力大小  
#define M 8  
#define N 8  
  
//设置坏巧克力块的位置  
#define X  4  
#define Y  4  
  
void print(char cho[M][N])  
{  
    //打印出巧克力形状  
    for (int i = 0; i= 0; i--)  
    {  
        if (row[i] != -1)  
        {  
            dm[0] = 'R';  
            dm[1] = i;  
            if (PreDispose(cho, dm) % 2 != 0)  
            {  
                printf("找到最佳步骤:\n");  
                return;  
            }  
        }  
    }  
    for (int j = N - 1; j >= 0; j--)  
    {  
        if (col[j] != -1)  
        {  
            dm[0] = 'C';  
            dm[1] = j;  
            if (PreDispose(cho, dm) % 2 != 0)  
            {  
                printf("找到最佳步骤:\n");  
                return;  
            }  
        }  
    }  
    //如果没有最佳步骤，则随便走一步  
    return;  
}  
  
//计算机掰巧克力的过程  
void Computer(char cho[M][N])  
{  
    char dm[2];  
    dm[0] = -1; dm[1] = -1;  
    //让计算机开始分析巧克力，并给出决策  
    Alaysize(cho, dm);  
    printf("计算机给出决策 %c %d\n", dm[0], dm[1]);  
    if (dm[0] == -1 && dm[1] == -1)  
    {  
        printf("计算机输了\n");  
    }  
    //掰巧克力  
    Execute(cho, dm[0], dm[1]);  
}  
  
int main()  
{  
    //制作巧克力  
    char cho[M][N];  
  
    char pos[10];  
  
    char cmd = 0;  
    int index = 0;  
  
    //设置坏巧克力  
    memset(cho, 0, M*N);  
    cho[X][Y] = 1;  
  
    //打印巧克力  
    print(cho);  
  
    printf("请输入命令:\n");  
    scanf("%s", pos);  
  
    while (1)  
    {  
        cmd = pos[0];  
        index = atoi(pos + 1);  
  
        if (cmd == 'Q' || cmd == 'q')break;  
  
        //掰巧克力  
        Execute(cho, cmd, index);  
        //打印出巧克力形状  
        print(cho);  
  
        //计算机处理  
        Computer(cho);  
        //打印出巧克力形状  
        print(cho);  
  
        printf("请输入命令:\n");  
        scanf("%s", pos);  
    }  
  
    return 0;  
}  

 

12.翻薄饼 有n张大小各不相同的薄饼，一张叠在另一张上面。允许大家把一个翻板插到一个薄饼下面，然后可以把板上面这叠薄饼翻个身。我们的目标是根据薄饼的大小重新安排它们位置，最大的薄饼要放在最下面。设计一个算法来解这个谜题。

解答：找到最大的薄饼，先将它翻到顶，然后全部翻过来。这样最大的薄饼就位于最下方，问题转化成将第二大的薄饼放在下方第二个位置。采用减治法（减一）思想，不断地执行该步骤。