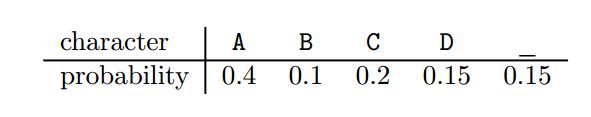算法设计与分析基础 第九章谜题
习题9.1
6.向下均分 有n>1个相同的缸，其中一个有W品脱的水，而别的缸为空。你被允许执行下列操作：取两个缸，然后把他们中的水在两个缸之间均分。目标是通过执行上述一系列操作，使得初始有水的缸中水最小化。完成这个任务的最好方法是什么？
解答：为了使初始有水的缸中（设为编号0）水最小，每次让它都和剩余的空缸进行均分，每一次操作都使缸中的水减少二分之一，这是减少最多的操作。当和所有的空缸进行均分之后，缸中剩余
品脱的水。这时其他的缸中的水都大于或者等于
品脱，我们无法对任意两个缸进行均分得到比
品脱更小的结果。
为什么这是全局最优的算法呢？换个角度考虑该问题，我们考虑如何使得1~n-1号空缸得到的总水量最大。那么每一次均分都应该是用空缸和0号缸进行均分，这样每一步都用一个空缸获得最大水量，而不是在1~n-1号缸内部进行均分，因为内部均分不仅不能获得更多的水，而且还可能使空缸的水变多。
7.谣言传播 有n个人，每个人都拥有不同的谣言。通过发电子信息，他们相互想共享所有的谣言。假定发送者会在信息中包含他已知的所有谣言，而且一条信息只有一个收信人。设计一个贪心算法，保证再给个人都能获得所有谣言的条件下，是发送的信息数最小。
解答：将这n个人标记为1, 2, …, n，按照1发信给2, 2发信给3, 3发信给4，…，n-1发信给n的方式发送谣言，该贪心算法基于每次发信都使得当前收信人掌握的谣言更多，最后由n将所有谣言发送给其他n-1个人。
发送信息总数为2n-2，这是最小的发信息数。因为每增加一个人，至少需要增加两次发送信息，当n=2是，发送信息数为2，归纳法可证明2n-2为最小发信息数。
8.巴切特砝码问题 求n个砝码{w1,w2,…,wn}的一个集合，使得它可以对天平上重量范围从1到W的任意整数负载进行称重。分别对下面两种条件求解：
a. 砝码只能放在天平的一边。
解答：当W=1，w1=1；当W=2，增加w2=2；当W=3，w1和w2可称重；当W=4，增加w3=4；…直到W=7，w1w2w3可称重…如下图所示，可将W转化为二进制表示对应相应砝码来称重。
可得wi=2^i-1，i=1,2,…n。可称重的范围是从1到2n-1.
b. 砝码能够放在天平的两边。
解答：由于砝码可以放天平的两端，所以不光可以做加法，还可以做减法，例如2可以通过3-1获得。{1,3}可以称重从1到4；{1,3,9}可以称重从1到13…
令wi=3^i-1，i=1,2,…n，可称重的范围是从1到(3n-1)/2.
习题9.2
5.设计一个求加权连通图的最大生成树算法，这是一种包含最大可能权重的树。
解答：将书中的各个权重变为相反数，然后求其最小生成树，可应用Prim算法或Kruskal算法求解。
11.斯坦纳树 4个村庄坐落在欧几里得平面上的一个单位正方形的4个顶点上。要求用最短的公路网把它们连接起来，使得每对村庄之间都有一条来连通的路径。求这样一个网络。
解答：
习题9.3
2a. 解下面这个单起点最短路径问题的实例，以顶点a作为起点。
解答：
| 树中顶点 |
余下的顶点 |
| a(-,0) |
b(-,∞) c(-,∞) d(a,7) e (-,∞) |
| d(a,7) |
b(d,7+2) c(d,7+5) e (-,∞) |
| b(d,9) |
c(d,12) e (-,∞) |
| c(d,12) |
e (c,12+6) |
| e (c,18) |
|
最短的路径和它们的长度：
从a到d：a-d, 长度为7；
从a到b：a-d-b， 长度为9；
从a到c：a-d-c， 长度为12；
从a到e：a-d-c-e， 长度为18.
习题9.4
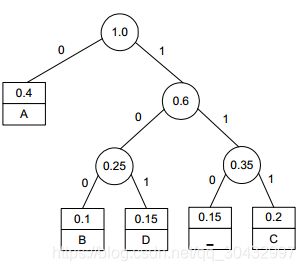
1. a对于下面的数据构造一套哈夫曼编码
解答：
| 字符 |
A |
B |
C |
D |
_ |
| 出现概率 |
0.4 |
0.1 |
0.2 |
0.15 |
0.15 |
| 代码字 |
0 |
100 |
111 |
101 |
110 |
b.用a中的编码对文本ABACABAD进行编码。
解答：0100011101000101
c.对于100010111001010用a中的编码进行解码。
解答：BAD_ADA
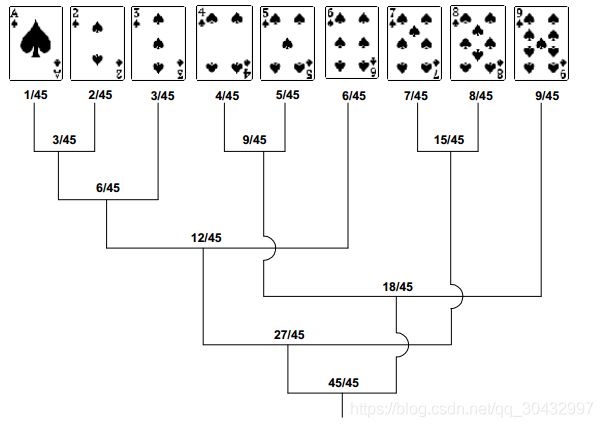
10.猜底牌 设计一种策略，使在下面的游戏中，期望提问的次数达到最小。有一副纸牌，是由1张A，2张2, 3张3, …,9张9组成的，一共包含45张牌。有人从这幅洗过的牌中抽出一张牌，问一连串可以回答是或否的问题来确定这张牌的点数。
解答：针对猜底牌问题，此处需要构建哈夫曼树，通过哈夫曼编码的长度来确定具体回答是或否的个数。根据哈夫曼编码0或者1来提问。例如，第一个问题可以是：
请问这张牌数字是4,5,9中的一个吗？
平均提问次数为：5/45+5*2/45+4*3/45+3*4/45+3*5/45+3*6/45+3*7/45+3*8/45+2*9/45=3
| 字符 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 出现概率 |
1/45 |
2/45 |
3/45 |
4/45 |
5/45 |
6/45 |
7/45 |
8/45 |
9/45 |
| 代码字 |
00000 |
00001 |
0001 |
100 |
101 |
001 |
010 |
011 |
11 |
