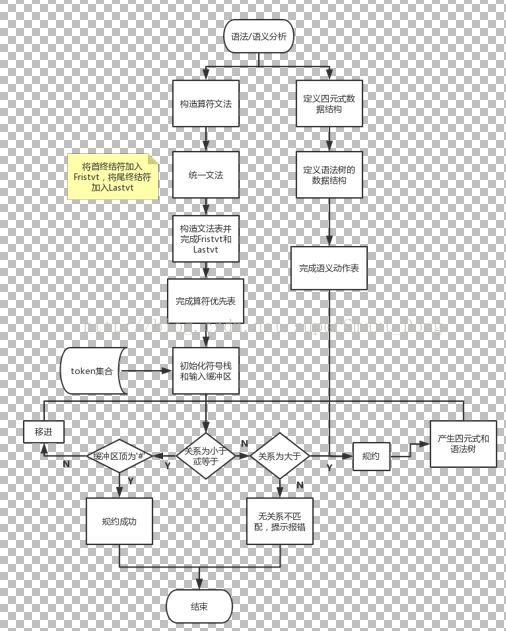
编译实验(二)语法/语义分析
通过词法分析,我们成功得到了一个完整的token 文件以及符号表,接下来要做的就是语法/语义分析。我们采用的分析方法是算符优先算法,实现这一个算法的前提是文法必须是算符优先文法,因此我们首先要做的事就是构造算符优先文法,文法结构如下:
1、构造文法并且初始化其各个属性。
class Grammar
{
public:
int getid(){ return id ; }
char * getINP(){ return INP; }
char *getOUP(){ return OUP; }
bool isbelong(string str) ; //是否属于终结符集合
vector getisEnd(){ return isEnd; }
private:
int id; //文法序号
char * INP; //产生式左部分
char * OUP;//产生式右部分数组
vector notEnd; //非终结符集合
vector isEnd; //终结符集合
}; 本次实验所用的算符文法 grammar 数组集合:
Grammar grammar[] = {
Grammar(0, "W", "# P #"),
Grammar(1, "P", "program id L"), //程序,标识符,程序体
Grammar(2, "L", "S ; L") ,//S语句 , L 语句表, A赋值语句,B 布尔表达式,E算术表达式
Grammar(2, "L", "S"),
Grammar(3, "S", "if B then S"),
Grammar(3, "S", "if B then L else S"),
Grammar(3, "S", "while B do S"),
Grammar(3, "S", "begin L end"),
Grammar(3, "S", "var D"),
Grammar(3, "S", "?"), //s->空 //10个
Grammar(3, "S", "A"),
Grammar(4, "D", "id : K ;"), //D 声明语句 , id标识符 ,K数据类型
Grammar(5, "K", "integer"),
Grammar(5, "K", "bool"),
Grammar(5, "K", "real"), //156
Grammar(6, "A", "id := E"),
Grammar(7, "E", "E + T"),
Grammar(7, "E", "T"),
Grammar(7, "E", "- E"),
Grammar(8, "B", "B or N"), //20
Grammar(8, "B", "N"),
Grammar(8, "B", "not B"), //R 布尔运算符
Grammar(9, "T", "T * F"),
Grammar(9, "T", "F"),
Grammar(10, "F", "( E )"), //25
Grammar(10, "F", "id"),
Grammar(11, "N", "N and M"),
Grammar(11, "N", "M"),
Grammar(12, "M", "( B )"),
Grammar(12, "M", "id < id"),//30
Grammar(12, "M", "id > id"),
Grammar(12, "M", "id <> id"),
Grammar(12, "M", "id <= id"),
Grammar(12, "M", "id >= id"),
Grammar(12, "M", "id = id"),
};例如Grammar(1, "P", "program id L"),表示P->program id L 产生式,程序中标识符、整形、浮点型和常数在产生式统一体现为”id”,文法序号用来区分产生式左部的非终结符,此文法中,非终结字符全用大写字母表示,终结字符全用小写字母表示,这样区分是否为终结符只需要判断字符串转化成大写后是否等于本身即可。
2、将所有文法根据产生式左部统一起来
完成了文法的构建,接下来要把产生式统一起来,结构如下:
class flGrammar
{
private:
vector isEnd;
string notEnd; //左产生式
int id;
public:
vector fristvt;
vector lastvt;
flGrammar(){};
int getid(){ return id; }
string getNotEnd(){ return notEnd; }
flGrammar(int id){ flInitGrammar(id); };
void flInitGrammar(int id);
bool isexistFirstvt(string str) //是否在fristvt和lastvt
{
for (int i = 0; i < fristvt.size(); i++)
if (str == fristvt[i])
return true;
return false;
}
bool isexistLastvt(string str);
}; 本次要做的主要任务为求得Fristvt和Lastvt的第一步,也就是把产生式第一个终结符加入到Fistvt,如果第一个是非终结符把第二个字符串姐加入到Fristvt,Lastvt同理。
通过初始化工作,得到一个整合起来的文法,例如 S->if B then S,S->begin L end,整合起来后得到notend=”S” ,isend={if then begin end},fristvt={if begin},lastvt={then end},其中flGrammar的属性id也就是文法序号。
3、构造文法表,完善Fristvt和lastvt
class flTable
{
public:
flTable();
~flTable();
void print(){
for (int i = 0; i < Grammar_Maxid; i++)
flgrammar[i]->print();
}
void finishGra(); //完成Fristvt & Lastvt
void printTable();
bool Match(vector,string &);
void printBuffer();
void printCreateTreeStack();
void printSignStack();
Tree * getGraTree(){ return GrammarTree; }
private:
flGrammar *flgrammar[Grammar_Maxid];
vector end; //终结符聚合
int **t_relation;
void initEnd();
bool isexistEnd(vecEnd str)
{
for (int i = 0; i < end.size(); i++)
if (str.end == end[i].end)
return true;
return false;
}
int findend(string str) ; //根据字符串查询终结符在end的中的索引
vector signStack; //符号栈
vector Buffer;//输入缓冲区
string getSignStackname(token t)
{
if (typeIsId(t.type))
return "id";
return t.name;
}
Tree *GrammarTree = NULL;
}; 其中flGrammar *flgrammar[Grammar_Maxid];也就是关于所有文法的集合,之前已经把产生式第一个终结符加入到Fristvt,把产生式最后一个终结符加入到Lastvt中。现在要完善Fristvt和Lastvt。从尾至头的遍历garmmar文法数组集合,把形如P->Q……这样非终结符Q打头的Fristvt集加入到P的Fristvt集里,形如P->……Q这样非终结符结尾的Q的Lastvt集加入到P的lastvt,在加入的过程中首先要判断要加入的终结符是否已经在了集合中。这就是bool flGrammar:: isexistFirstvt(string str) 的作用,如果已经在集合中就不用再加入进去了。
4、初始化终结符集合,完成算符优先表
void flTable::initEnd();终结符集合比较简单,只需要遍历文法的终结符集合即可。初始化算符优先表,把P->…Qa… 这样的Lastvt(Q)中所有元素> a ,把P->…aQ…这样的a
细化算符优先表int **t_relation;步骤
1、遍历grammar文法集合,从第0个文法开始,将其产生式右部分进行字符串分割,得到一个该产生式右部字符集合,遍历该字符集合,从第i=0个字符开始判断是不是终结符,如果是,再判断第i+1个字符是不是非终结符,如果是,第i个终结符小于第i+1个非终结符的Fristvt集合,如果第i+1是终结符,则第i个等于第i+1个。
2、如果第i个是非终结符则第i个的非终结符的Lastvt集合大于第i+1个字符。
3、再次遍历一遍文法,如果第i=0个字符为终结符且第i+1个为非终结符且第i+2个为终结符,则第i个终结符等于第i+2个终结符。
注意:终结符在算符优先表的位置也就是在vector<vecEnd> end; //终结符集合中的位置,所以有 int flTable:: findend(string str)的作用就是查找终结符在终结符集合中的索引。
5、初始化符号栈,输入缓冲区,根据算符优先表完成规约
先自定义一个有 “#”的token对象,将#压入栈中和缓冲区中,再将词法分析中产生的token集合逆序推入缓冲区。我们知道,在规约整个过程中都是栈与缓冲区的终结符之间的关系比较,与非终结符无关。所以规约时,只需要把栈中元素推出去即可,无需再把非终结符压入栈中。
当栈顶元素与缓冲区顶元素比较,如果小于或等于,把缓冲区顶元素移进到栈中。如果大于则栈顶指针top下移,top和top+1元素进行比较直到比较到小于时,将top之后的元素全部从栈中推出。栈顶元素与缓冲区顶元素无关系时,则指明语法出错。当且仅当关系为等于号且缓冲区顶部元素为#时表明成功规约。至此语法分析结束。
6、语义分析:完成语义动作表以及四元式数据结构
四元式结构如下:其中op代表第一元素的字符形式,code代表第一元素代码形式。ConvertOpToCode()方法是根据op给code赋值。完成后,定义一个四元式集合,语义分析就是完成代码关于四元式集合的生成。
struct GenStruct
{
int label; //四元式序号
string op;
int code; //第一元素
string addr1="0"; //第二元素
string addr2="0"; //第三元素
string result="0";//第四元素
int out_port = 0; //记录该四元式是否为一个基本块的入口,是则为1,否则为0。
void ConvertOpToCode(string);
GenStruct(int l){ label = l; }
GenStruct(int l,string op,string a1,string a2,string res){
label = l, this->op=op, ConvertOpToCode(op), addr1 = a1, addr2 = a2, result = res;
}
};语义动作表代码在语法分析中规约的时候完成:
void GrammarAction(TreeNode *pNew, vector pushend,int index) //语义动作 index代表其文法索引, pushend代表各个结点 pNew 根结点
{
string value1;
string backpatchfalse;
switch (index)
{
#pragma region ...
case 0:
pNew->nextlist = pushend[1].nextlist;
break;
case 1:
pNew->nextlist = pushend[0].nextlist;
break;
case 2:
pNew->nextlist = pushend[0].nextlist;
pNew->fristnextquad = pushend[2].fristnextquad;
break;
case 3:
pNew->nextlist = pushend[0].nextlist;
pNew->fristnextquad = pushend[2].fristnextquad;
break;
//S
case 4: //if B then S
backpatch(pushend[pushend.size() - 2].truelist, pushend[pushend.size() - 2].nextquad);
pNew->nextlist = merge(pushend[0].nextlist, pushend[pushend.size() - 2].falselist);
pNew->fristnextquad = pushend[pushend.size() - 2]].fristnextquad;
break;
case 5://if B then L else S,then 要跳转到 else后面
int2str(stoi(pushend[2].nextquad)+1,backpatchfalse);
backpatch(pushend[pushend.size() - 2].truelist, pushend[pushend.size() - 2].nextquad);
backpatch(pushend[pushend.size() - 2].falselist, backpatchfalse);
//backpatch(pushend[pushend.size() - 2].falselist, pushend[0].fristnextquad);
pNew->nextlist = merge(pushend[0].nextlist, pushend[pushend.size() - 2].falselist);
CreateGen("j", "0", "0", pushend[0].nextquad);
pNew->nextquad = getNextquad();
//把getnextquad的产生式插入到pushend[2].nextquad ,把13加入到7后面8
InsertGentoIndex(getNextquad(), pushend[2].nextquad);
pNew->fristnextquad = pushend[pushend.size() - 2]].fristnextquad;
break;
case 6://s->while B do S
/* backpatch(pushend[0].nextlist,pushend[2].fristnextquad);*/
backpatch(pushend[2].truelist, pushend[2].nextquad);
pNew->nextlist = pushend[2].falselist;
CreateGen("j", "0", "0", pushend[2].fristnextquad);
pNew->nextquad = getNextquad();
backpatch(pushend[2].falselist, getNextquad());
break;
case 7://begin S end
pNew->nextlist = pushend[1].nextlist;
break;
case 8://var D
break;
case 9:// ?
break;
case 10://S->A
break;
case 11: //D:->id:K
break;
case 12://k->integer
break;
case 13://k->integer
break;
case 14://k->integer
break;
case 15://A-> id:=E
CreateGen(pushend[1].data.name, pushend[0].value, "0", pushend[2].data.name);
pNew->nextquad = getNextquad();
break;
case 16://E->E+T
value1 = NewTempStruct();
CreateGen("+", pushend[2].value, pushend[0].value, value1);
pNew->value = value1;
pNew->nextquad = getNextquad();
break;
case 17:
pNew->value = pushend[0].value;
break;
#pragma endregion
case 18: //E->-E
value1 = NewTempStruct();
CreateGen("-","0", pushend[0].value, value1);
pNew->nextquad = getNextquad();
pNew->value = value1;
break;
case 19://B-> B or N
backpatch(pushend[pushend.size() - 1].falselist, pushend[pushend.size() - 1].nextquad);
pNew->truelist = merge(pushend[pushend.size() - 1].truelist, pushend[0].truelist);
pNew->falselist = pushend[0].falselist;
pNew->fristnextquad = pushend[2].fristnextquad;
break;
case 20://B->N
pNew->falselist = pushend[0].falselist;
pNew->truelist = pushend[0].truelist;
pNew->value = pushend[0].value;
break;
case 21://B->not B
pNew->falselist = pushend[0].truelist;
pNew->truelist = pushend[0].falselist;
pNew->value = pushend[0].value;
break;
case 22: //T->T*F
value1 = NewTempStruct();
CreateGen("*", pushend[2].value, pushend[0].value, value1);
pNew->value = value1;
pNew->nextquad = getNextquad();
break;
case 23://T->F
pNew->falselist = pushend[0].falselist;
pNew->truelist = pushend[0].truelist;
pNew->value = pushend[0].value;
break;
case 24://F->(E)
pNew->falselist = pushend[1].falselist;
pNew->truelist = pushend[1].truelist;
pNew->value = pushend[1].value;
break;
case 25://F->id
pNew->value = pushend[0].data.name;
break;
case 26://N->N and M
backpatch(pushend[pushend.size() - 1].truelist, pushend[pushend.size() - 1].nextquad);
pNew->falselist = merge(pushend[pushend.size() - 1].falselist, pushend[0].falselist);
pNew->truelist = pushend[0].truelist;
pNew->fristnextquad = pushend[2].fristnextquad;
break;
case 27:
pNew->falselist = pushend[0].falselist;
pNew->truelist = pushend[0].truelist;
pNew->value = pushend[0].value;
break;
case 28: //M->(B)
pNew->falselist = pushend[1].falselist;
pNew->truelist = pushend[1].truelist;
pNew->value = pushend[1].value;
break;
case 29: //M->id 其中merge作用是将两集合合并并返回,backpatch作用是回填,把新值回填到指定四元式集合的第四元素中。CreateGen()产生四元式并加入到四元式集合中,void InsertGentoIndex(string sel,string desti)将四元式中转移到四元式集合中的指定位置,其中sel代表所在位置,destin代表要转移到的位置。
注意:在转移过程中要把在destin和sel之间的所有四元式的label加1,判断并且跳转语句的四元式的第四元素是否在在destin和sel之间内,如果在将该四元式的第四元素+1,最后删除原本的四元式。语义动作表是在规约前完成,找出规约时所用的产生式,根据产生式的索引完成指定的动作。可以根据规约时的终结符集合和产生式中终结符集合是否降等来判断所用的产生式是哪一条。
7、语法分析:定义(语法)树的数据结构
因为语法所用的规约只把终结符推出栈,与非终结符无关。但是这样就无法进行自下而上的属性赋值,也就无法完成语义动作。用建立树的方式,在规约的时候把要规约的符号作为孩子,而查询出的规约的产生式左部的非终结符作为根节点。规约时完成对语法树的建立偶同时完成语法动作(也就是四元式产生).
struct TreeNode
{
TreeNode()
{
fristnextquad = getNextquad();
nextquad = getNextquad();
value = data.name;
sibling = NULL;
child = NULL;
}
DataType data;
TreeNode * sibling; //右兄弟结点
TreeNode * child; //左子结点
string nextquad; //完成规约时的四元式地址
string fristnextquad; //完成规约前的四元式地址
string value; //代表的值,产生式第四元素如T1,T2
vectornextlist;
vectortruelist; //真出口集
vectorfalselist; //出口集
}; 其中getNextquad()为四元式集合长度,也就是下一条要产生四元式的地址,DataType为token。完成了数据结构的定义,在规约时,就把每一个要规约的元素建立一个结点(兄弟结点),找到规约对应的产生式,根结点也就是该产生式的左部非终结符。也就是说在语法规约的时候,完成对树的建立,完成规约时相应的语法动作,最终完成规约,建立好语法树。干脆。重新再建立一个符号栈,不过符号栈中元素不在是token而是TreeNode,和原本的符号栈的区别就在于把非终结符也加入到了里面,而不是与非终结符无关。