排序算法总结
文章目录
- 选择排序
- 思想
- 代码:
- 冒泡排序:
- 思路
- 代码
- 优化
- 快速排序
- 代码:
- STL中的sort和cmp:
- 例题
- 年龄排序:
- 归并排序
- 思路
- 代码:
- 求逆序对:
- 堆排序
- 思路:
- 桶排序:
排序,一种经常使用的算法,分为稳定算法和不稳定算法。
稳定算法:如果ai=aj,在排序前i
不稳定算法:如果ai=aj,在排序前i
至于如何判断这种排序方法是否稳定,只需要看它在交换时是否是临项交换。如果是,这方法就是稳定的。否则,就不稳定。
#TOC
选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是O(n²)的时间复杂度,而且是不稳定排序。唯一的好处可能就是不占用额外的内存空间了吧。
思想
每一趟从待排序的数据元素中选出最大的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
如图所示:
代码:
#include
using namespace std;
int n,a[1005];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i 很明显,这是一个不稳定排序。
冒泡排序:
一种比选择排序更好的方法,虽然时间复杂度也是O(n²),但冒泡排序是稳定排序。
思路
依次比较相邻的两个数,将比较小的数放在前面,比较大的数放在后面。 每一次循环,最大的一个数字就会到最后去。所以我们需要循环n次。
![]()
由于这种算法是重的沉下去,轻的浮上来,所以叫做冒泡排序。
代码
#include
using namespace std;
int n,a[1005];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n-i;j++) {
if(a[j]>a[j+1])
swap(a[j],a[j+1]);
}
}
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
优化
其实,当每一次循环没有发生交换,这个序列就是有序的了。
#include
using namespace std;
int n,a[1005];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++) {
bool l=0;
for(int j=1;j<=n-i;j++) {
if(a[j]>a[j+1])
swap(a[j],a[j+1]),l=1;
}
if(l==0)
break;
}
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
快速排序
说白了:就是让一个数当“老大”,比它小的数做坐它左边,比它大的数坐它右边。这样这个数就会变换到它该在的位置。由于这个数变换到它该在的位置不需要n次,所以快速排序的时间复杂度不是O(n²),是O(n log2 n)。
![]()
如果上图看不懂,看下面这张:
![]()
代码:
#include
using namespace std;
int n,a[1005];
void qsort(int l,int r) {
if(l>r) return ;
int sum=a[l],i=l,j=r;
while(i!=j) {
while(a[j]>=sum && i STL中的sort和cmp:
在STL中,有快速排序sort,有3个参数,第一个是起点指针,第二个是终点,第三个是cmp(排序的规矩)。如果第3个参数为空,默认的是从小到大排序。上一个代码就可以写成:
#include
using namespace std;
int n,a[1005];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+n+1);
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
如果要从小到大,如下:
#include
using namespace std;
int n,a[1005];
bool cmp(int x,int y) {
return x>y;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
多了一个cmp。
例题
来一道例题,熟悉一下cmp。
年龄排序:
输入 n (n<=100)个学生的信息,包括姓名、性别、出生年月。要求按年龄从小到大依次输出这些学生的信息。数据保证没有学生同年同月出生。
这题没什么可以说,就是要注意cmp的写法。
代码:
#include
using namespace std;
int n;
struct node{
char name[15],x[15];
int year,month;
}a[105];
bool cmp(node x,node y) {
if(x.year 归并排序
归并排序是稳定的,且时间复杂度是O(n log2 n)。
思路
是分治法的一个典型的运用。
1.将序列二分。
2.合并成有序序列。它合并时是将将要合并的这两个序列的第一个元素进行比较,谁大谁就进预备数组,直到某个序列出完,然后把另一个数组的剩下的所有的都进预备数组。

代码:
#include
using namespace std;
int n,a[100005],r[100005];
void msort(int s,int t) {
if(s==t)
return ;
int mid=(s+t)/2;
msort(s,mid),msort(mid+1,t);
int i=s,j=mid+1,k=s;
while(i<=mid && j<=t) {
if(a[i]<=a[j])
r[k]=a[i],k++,i++;
else
r[k]=a[j],k++,j++;
}
while(i<=mid)
r[k]=a[i],k++,i++;
while(j<=t)
r[k]=a[j],k++,j++;
for(int i=s;i<=t;i++)
a[i]=r[i];
return ;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
msort(1,n);
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
求逆序对:
给定一个序列a1,a2,…,an,如果存在 i
这种题我们其实可以用冒泡排序,每交换一次,ans就++。
代码:
#include
using namespace std;
int n,a[100005];
long long ans;
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n-i;j++) {
if(a[j]>a[j+1])
swap(a[j],a[j+1]),ans++;
}
}
printf("%lld",ans);
return 0;
}
但这速度太慢了,因为它是一个一个找的,十分慢。
我们可以用归并排序。
假设左边序列为{3,4,7,9},右边为{1,5,8,10};
那我们的第一步是比较1和3,因为1<3,所以1入预备数组。我们可以发现1和左边序列都成逆序对,所以我们可以一下子找到4对了,这也是归并排序找逆序对快的原因:它是一串一串找的。
代码:
#include
using namespace std;
int n,a[100005],r[100005];
long long ans;
void msort(int s,int t) {
if(s==t)
return ;
int mid=(s+t)/2;
msort(s,mid),msort(mid+1,t);
int i=s,j=mid+1,k=s;
while(i<=mid && j<=t) {
if(a[i]<=a[j])
r[k]=a[i],k++,i++;
else {
r[k]=a[j],k++,j++;
ans+=mid-i+1;
}
}
while(i<=mid)
r[k]=a[i],k++,i++;
while(j<=t)
r[k]=a[j],k++,j++;
for(int i=s;i<=t;i++)
a[i]=r[i];
return ;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
msort(1,n);
printf("%lld",ans);
return 0;
}
堆排序
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
![]()
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子:
![]()
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
**小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] **
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤。
思路:
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
步骤一:构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
1.假设给定无序序列结构如下

2.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
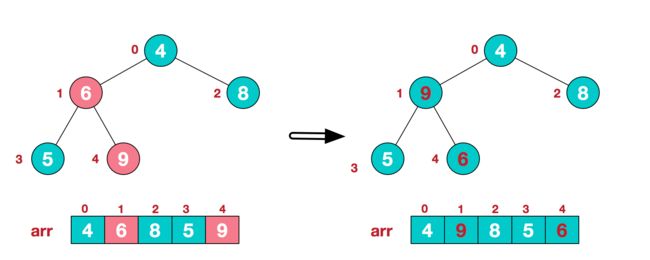
3.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
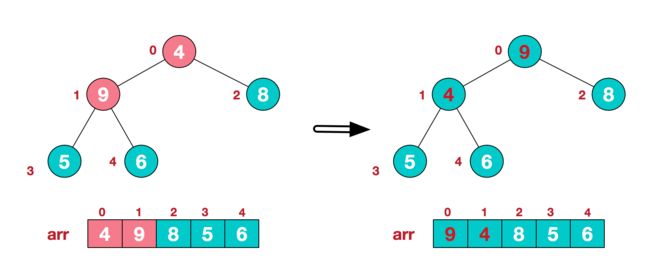
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
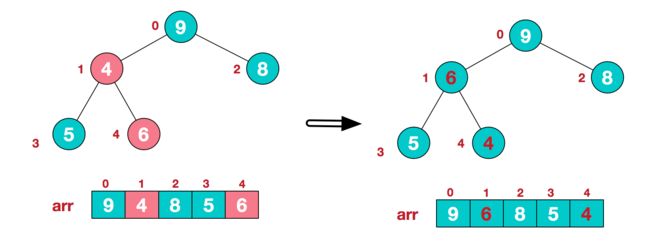
此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二:将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
简单总结一下堆排序的基本思路:
1.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
2.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
代码请自己写。
桶排序:
在一个只有非负数(n<=100000)的序列中,我们可以用桶排序。
先定义一个数组z[100005];
假设z[i]是一个桶。
我们在输入是就将相应的数装到相应的桶中。
int n,z[100005]
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) {
int t;
scanf("%d",&t);
z[t]++;
}
}
至于输出:
for(int i=1;i<=100000;i++) {
for(int j=1;j<=z[i];j++)
printf("%d ",i);
}
如果要去重:
for(int i=1;i<=100000;i++) {
if(z[i])
printf("%d ",i);
}
具体代码:
#include
using namespace std;
int n,z[100005];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) {
int t;
scanf("%d",&t);
z[t]++;
}
for(int i=1;i<=100000;i++) {
if(z[i])
printf("%d ",i);
}
return 0;
}
桶排序非常快,O(n),但它有一个弊端,它不能排负数,而且如果数的范围非常大的话,空间就会浪费很多,所以使用须慎重。