论文《node2vec: Scalable Feature Learning for Networks》提出了node2vec算法,node2ve算法通过表征2种顶点间的关系,得到顶点的低维向量表示,
- homophily equivalence
- structural equivalence
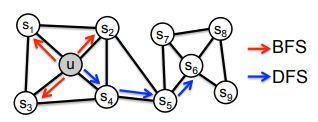
homophily equivalence表明直接相连的顶点或是在同一community中的顶点,其embeddings应该比较靠近,如图所示,顶点$u$、$s_1$、$s_2$、$s_3$和$s_4$之间直接相连且属于同一community,因此,这些顶点的embedding在特征空间中比较靠近;structural equivalence表面在图中具有相似结构特征的顶点(顶点间不必直接相连,可以离得很远),其embeddings应该比较靠近,例如,顶点$u$和$s_6$都是各自所在community的中心,具有形似的结构特征,因此,顶点$u$和$s_6$的embedding在特征空间中比较靠近。node2vec算法design a flexible neighborhood sampling strategy which allows us to smoothly interpolate between BFS and DFS。
特征学习框架
Node2vec算法希望,在给定顶点的条件下,其领域内的顶点出现的概率最大。即优化目标函数式(1),
$$\begin{equation}\max_f\sum_{u \in V}\log Pr(N_S(u)|f(u)) \tag{1}\end{equation}$$
对于每一个源顶点$u\in V$,$N_S(u)$为根据采样策略$S$得到的邻域。
为了简化目标函数,论文提出了2个假设,
- 条件独立性
- 特征空间对称性
假设1表示当源顶点$u$的特征表示$f(u)$给定时,$Pr(n_i|f(u))$和$Pr(n_j|f(u))$无关($n_i\in N_S(u),n_j \in N_S(u),i\neq j$)。因此,$Pr(N_S(u)|f(u))$可写为式(2),
$$\begin{equation}Pr(N_S(u)|f(u))=\Pi_{n_i \in N_S(u)}Pr(n_i|f(u))\tag{2}\end{equation}$$
假设2说明源顶点和其邻域内任一顶点,相互之间的影响是相同的。最自然的想法就是将$Pr(n_i|f(u))$写为式(3),
$$\begin{equation}Pr(n_i|f(u))=\frac{exp(f(n_i)^\top f(u))}{\sum_{v \in V}exp(f(v)^\top f(u))}\tag{3}\end{equation}$$
因此,node2vec算法就需要解决两个问题,
- 给定一个源顶点$u$,使用什么样的采样策略$S$得到其邻域$N_S(u)$;
- 如何优化目标函数。
对于第二个问题,可以参考基于negative sampling的skip-gram模型进行求解,关键是确定采样策略$S$。
邻域采样策略
node2vec算法提出了有偏的随机游走,通过引入2个超参数$p$和$q$来平衡BFS和DFS,从顶点$v$有做到顶点$x$的转移概率为式(4),
$$ \begin{equation}p(c_i=x|c_{i-1}=v) = \begin{cases} \frac{\pi_{vx}}{Z}, if \quad (v,x)\in E \\ 0, otherwise \end{cases}\tag{4}\end{equation} $$
其中,$x$表示游走过程中的当前顶点,$t$和$v$分别为$x$前一时刻的顶点和下一时刻将要游走到的顶点,$\pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx}$,$w_{vx}$为边(v,x)的权值,$\alpha_{pq}(t,x)$定义如下,
$$\begin{equation}\alpha_{pq}(t,x)=\begin{cases}\frac{1}{p}, if \quad d_{tx}=0\\1,if \quad d_{tx}=1\\ \frac{1}{q},if \quad d_{tx}=2\end{cases}\tag{5}\end{equation}$$
其中,$d_{tx}=0$表示顶点$t$和$x$相同,$d_{tx}=1$表示顶点$t$和$x$之间存在之间相连的边,$d_{tx}=0$表示顶点$t$和$x$不存在直接相连的边。
如图所示,在一个无权图中(可以看作是所有边的权值为1),在一次游走过程中,刚从顶点$t$游走到$v$,在下一时刻,可以游走到4个不同的顶点,$t$、$x_1$、$x_2$和$x_3$,转移概率分别为$\frac{1}{p}$、$1$、$\frac{1}{q}$和$\frac{1}{q}$。
超参数$p$和$q$ control how fast the walk explores and leaves the neighborhood of starting node $u$。$p$越小,随机游走采样的顶点越可能靠近起始顶点;而$q$越小,随机游走采样的顶点越可能远离起始顶点。
代码实现
import networkx as nx
import numpy as np
import random
p = 1
q = 2
def gen_graph():
g = nx.Graph()
g = nx.DiGraph()
g.add_weighted_edges_from([(1, 2, 0.5), (2, 3, 1.5), (4, 1, 1.0), (2, 4, 0.5), (4, 5, 1.0)])
g.add_weighted_edges_from([(2, 1, 0.5), (3, 2, 1.5), (1, 4, 1.0), (4, 2, 0.5), (5, 4, 1.0)])
return g
def get_alias_edge(g, prev, cur):
unnormalized_probs = []
for cur_nbr in g.neighbors(cur):
if cur_nbr == prev:
unnormalized_probs.append(g[cur][cur_nbr]['weight']/p)
elif g.has_edge(cur_nbr, prev):
unnormalized_probs.append(g[cur][cur_nbr]['weight'])
else:
unnormalized_probs.append(g[cur][cur_nbr]['weight']/q)
norm = sum(unnormalized_probs)
normalized_probs = [float(prob)/norm for prob in unnormalized_probs]
return alias_setup(normalized_probs)
def alias_setup(ws):
'''
Compute utility lists for non-uniform sampling from discrete distributions.
Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
for details
'''
K = len(ws)
probs = np.zeros(K, dtype=np.float32)
alias = np.zeros(K, dtype=np.int32)
smaller = []
larger = []
for kk, prob in enumerate(probs):
probs[kk] = K*prob
if probs[kk] < 1.0:
smaller.append(kk)
else:
larger.append(kk)
while len(smaller) > 0 and len(larger) > 0:
small = smaller.pop()
large = larger.pop()
alias[small] = large
probs[large] = probs[large] + probs[small] - 1.0
if probs[large] < 1.0:
smaller.append(large)
else:
larger.append(large)
return alias, probs
def alias_draw(J, q):
'''
Draw sample from a non-uniform discrete distribution using alias sampling.
'''
K = len(J)
kk = int(np.floor(np.random.rand()*K))
if np.random.rand() < q[kk]:
return kk
else:
return J[kk]
def alias_draw(alias, probs):
num = len(alias)
k = int(np.floor(np.random.rand() * num))
if np.random.rand() < probs[k]:
return k
else:
return alias[k]
def preprocess_transition_probs(g):
'''
Preprocessing of transition probabilities for guiding the random walks.
'''
alias_nodes = {}
for node in g.nodes():
unnormalized_probs = [g[node][nbr]['weight']
for nbr in g.neighbors(node)]
norm= sum(unnormalized_probs)
normalized_probs = [
float(u_prob)/norm for u_prob in unnormalized_probs]
alias_nodes[node] = alias_setup(normalized_probs)
alias_edges = {}
for edge in g.edges():
alias_edges[edge] = get_alias_edge(g, edge[0], edge[1])
return alias_nodes, alias_edges
def node2vec_walk(g, walk_length, start_node, alias_nodes, alias_edges):
'''
Simulate a random walk starting from start node.
'''
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(g.neighbors(cur))
if len(cur_nbrs) > 0:
if len(walk) == 1:
walk.append(
cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])])
else:
prev = walk[-2]
pos = (prev, cur)
next = cur_nbrs[alias_draw(alias_edges[pos][0], alias_edges[pos][1])]
walk.append(next)
else:
break
return walk
def simulate_walks(g, num_walks, walk_length, alias_nodes, alias_edges):
'''
Repeatedly simulate random walks from each node.
'''
walks = []
nodes = list(g.nodes())
print('Walk iteration:')
for walk_iter in range(num_walks):
print("iteration: {} / {}".format(walk_iter + 1, num_walks))
random.shuffle(nodes)
for node in nodes:
walks.append(node2vec_walk(g, walk_length=walk_length, start_node=node, alias_nodes=alias_nodes, alias_edges=alias_edges))
return walks
if __name__ == '__main__':
g = gen_graph()
alias_nodes, alias_edges = preprocess_transition_probs(g)
walks = simulate_walks(g, 2, 3, alias_nodes, alias_edges)
print(walks)
# Walk iteration:
# iteration: 1 / 2
# iteration: 2 / 2
# [[5, 4, 1], [2, 3, 2], [4, 1, 2], [3, 2, 3], [1, 2, 3], [4, 1, 2], [3, 2, 3], [1, 2, 3], [2, 3, 2], [5, 4, 1]]参考
- node2vec: Scalable Feature Learning for Networks
- https://github.com/thunlp/Ope...