1202-2019-算法-迪杰斯特拉算法（最短路径算法-Dijkstra算法）

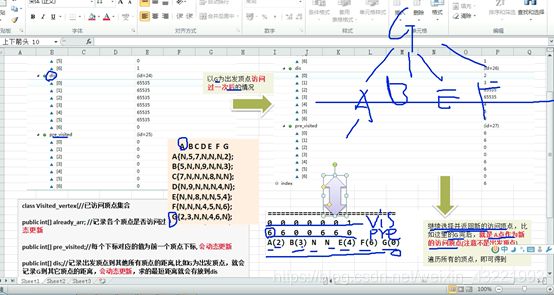
核心是动态更新三个数组：
① 是否已经访问过。
② 从G到任意一个点的最短距离。
③ 每一个结点的前一个结点的下标

代码的关键：
假如G为起点，先到可以直接到达的顶点，再找路径最短的那个顶点到其他没有到过的顶点。

package Dijkstra;

import java.util.Arrays;

/**
 * @author pdzz
 * @create 2019-12-02 17:11
 */
public class Dijkstra {

    public static void main(String[] args) {
        char[] vertex = {'A','B','C','D','E','F','G'};
        int[][] matrix = new int[vertex.length][vertex.length];
        final int N = 65535;//表示不可连接
        matrix[0] = new int[]{N,5,7,N,N,N,2};
        matrix[1] = new int[]{5,N,N,9,N,N,3};
        matrix[2] = new int[]{7,N,N,N,8,N,N};
        matrix[3] = new int[]{N,9,N,N,N,4,N};
        matrix[4] = new int[]{N,N,8,N,N,5,4};
        matrix[5] = new int[]{N,N,N,4,5,N,6};
        matrix[6] = new int[]{2,3,N,N,4,6,N};

        Graph graph = new Graph(vertex,matrix);
        //graph.showGraph();
        graph.dijkstra(6);
        graph.show();

    }

}
class VisitedVertex{
    //记录当前下标的顶点是否访问过
    public int[] already_arr;
    //每一个下标对应的值为前一个顶点的下标
    public int[] pre_visited;
    //记录出发顶点到其他顶点的距离
    public int[] dis;


    public VisitedVertex(int length,int index){
        this.already_arr = new int[length];
        this.pre_visited = new int[length];
        this.dis = new int[length];
        //初始化dis数组,让除了自己下标为0以外别的都为 N = 65535;
        Arrays.fill(dis,65535);
        this.already_arr[index] = 1;
        this.dis[index] = 0;

    }
  
    public boolean in(int index){
        /**
        *@Description 判断是否访问过
        *@Param [index]
        *@Return boolean
        *@Author pdzz
        *@Date 2019/12/2
        *@Time 17:35
        */
        return already_arr[index] == 1;
    }




    public void updateDis(int index,int len){/**
        *@Description 更新节点之间的距离
        *@Param [index, len]
        *@Return void
        *@Author pdzz
        *@Date 2019/12/2
        *@Time 17:36
        */
        dis[index] = len;
    }

    public void updatePre(int pre,int index){
        //更新节点的前驱节点
        pre_visited[pre] = index;
    }

    public int getDis(int index){
        //返回index的距离
        return dis[index];
    }
    public int updateArr(){
        int min = 65535;
        int index = 0;
        for (int i = 0; i < already_arr.length; i++) {
            if (already_arr[i] == 0 && dis[i] < min){
                min = dis[i];
                index = i;
            }
        }
        //找到最小的值了，下标的值为index，把它标记为访问过，继续调用update(index)
        //计算以index为起点到新的没有访问过的节点的最短路径。
        already_arr[index] = 1;
        return index;
    }

    public void show(){
        System.out.println(Arrays.toString(already_arr));
        System.out.println(Arrays.toString(pre_visited));
        System.out.println(Arrays.toString(dis));
    }

}

class Graph{
    private char[] vertex;
    private int[][] martix;
    VisitedVertex visitedVertex;

    public Graph(char[] vertex,int[][] martix){
        this.vertex = vertex;
        this.martix = martix;
    }

    public void showGraph(){
        for (int[] link:martix) {
            System.out.println(Arrays.toString(link));
        }
    }

    public void dijkstra(int index){

        visitedVertex = new VisitedVertex(vertex.length, index);
        update(index);
        for (int i = 1; i < vertex.length; i++) {
            index = visitedVertex.updateArr();
            update(index);
        }
    }

    public void update(int index){
        int len = 0;
        for (int i = 0; i < martix[index].length; i++) {
            //出发顶点到index的距离再加上index到i顶点的距离。
            len = visitedVertex.dis[index] + martix[index][i];
            if (!visitedVertex.in(i) && len < visitedVertex.getDis(i)){
                //更新距离
                visitedVertex.updatePre(i,index);
                visitedVertex.updateDis(i,len);
            }
        }
    }
    public void show(){
        visitedVertex.show();
    }

}

来自尚硅谷韩顺平老师的Java数据结构的视频