树与二叉树基础知识大全解

序言

2019年9月3日11:31:25 接下来进入树的章节 首先主要是学习树与二叉树的基础知识，为后续二叉树的应用打好铺垫；BST树；AVL树；以及红黑树等。

数据结构中知识繁杂，但是都很重要。毕竟数据结构与算法 是我们计算机专业最重要的一门课。来，先看一眼下图：
曾经有一个 建工转行要当程序员的老哥问我，当一个挣大钱的程序员需要学哪些内容？我给他拿出了上图，他大为不解的 问我：为什么不是什么 C C++等？唉 没有一个强大的数据结构功底，以及灵活应变的算法思想 这样的程序员是 没有内涵、没有灵魂的，顶多充其量 是个“码农”。上图所示，虽是看着复杂，然而这都是 非常基础的内容了，还希望大家学习的时候 一步一个脚印，人可以骗别人，可是能骗得了自己吗？

注：前几天，我已经把《DSA之十大排序算法系列》全部的内容更新完了，以及附带了自己亲自写的源代码 都是经过测试过的。不管是 代码或者是内容上的问题，都可以给我留言，我不想把当程序员当成一种职业 我更喜欢的可能就是：这是我的爱好。对了：我的源代码都放在了GitHub上 DSA之十大排序算法系列

话不多说：学习 开始

树的定义及常见概念

定义

在我们现实生活，除了排队买包子的队列、火车进站出站之栈、又或者是麻将桌上的自己的牌之线性表等等的一对一的线性结构。我们很常见的 家族族谱、生物基因重组等都是很多一对多的情况需要处理，因此这里 需要研究一对多的数据结构来解决这类问题。

注：这里参考教材有：严奶奶的数据结构 和 邓公的DSA。

之所以被称为树：是因为它看起来像一棵倒挂的树，也就是说它是根在上，而叶子向下的。树 是有着n (n>=0)个结点的有限集合。当n=0 时为空树。 n!=0时，在任意一颗非空的树中：

1. 有且仅有一个特定的成为根root 的结点（没有父结点的结点称为根结点）。
2. 每个结点有零个或多个子结点；每一个非根结点有且只有一个父结点。
3. 当n>1时， 除了根结点外，其余结点又可以分为m > 0个互不相交的有限集，T1、T2、T3····Tm, 其中的每一有限集又是一棵树，并且称为根root的子树 SubTree 。同时对于这棵树而言 也只有这么一个root节点，而m的值并无限制。
   如下图所示：
   

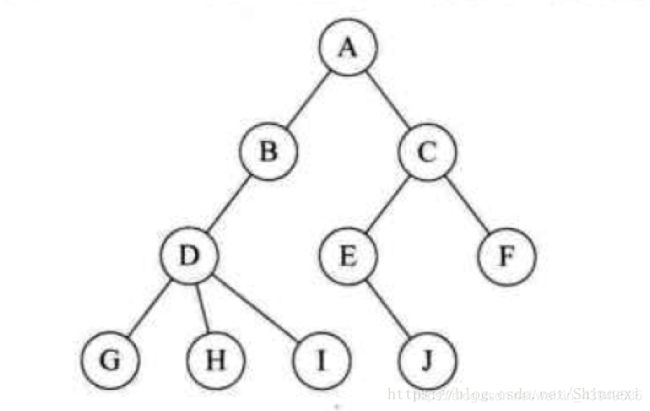
一棵树的定义从实质上来看：也是一种递归调用的经典应用，也即在树的定义的同时也使用到了树的概念。如下图中子树 T1 和 子树 T2 就是根结点A的子树，同时D、G、H、I组成的树又是以B为根节点的子树，E、J、F组成的树又是以C为根节点的另一个子树。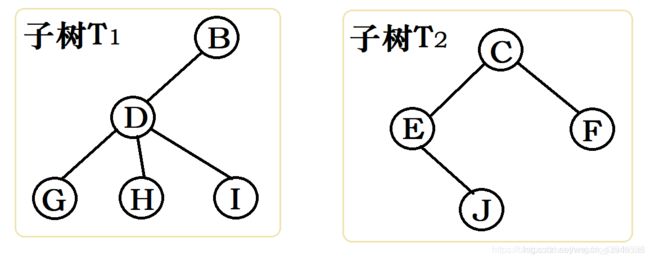

树的常见概念

结点的度—— —结点拥有的子树数称为结点的度（Degree）
树的度 —— 一棵树中最大的结点度数
双亲—— 孩子结点的上层结点叫该结点的双亲
兄弟—— 同一双亲的孩子之间互成为兄弟
祖先—— 结点的祖先是从根到该结点所经分支上的所有结点
子孙—— 以某结点为根的子树中的任一结点都成为该结点的子孙
结点的高度—— 从叶结点开始自底向上逐层累加。
结点的深度—— 从根节点开始自顶向下逐层累加。
结点的层次—— 从根结点算起，根为第一层，它的孩子为第二层……
堂兄弟—— 其双亲在同一层的结点互称为堂兄弟。
树的深度/高度—— 树中结点的最大层次数
有序树—— 如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。
森林—— m(m > 0)棵互不相交的树的集合，也即多棵树的集合
路径—— 两个结点之间的结点序列，不包括两个端点。
路径长度—— 两个节点之间的边数。

树的结点

结点类型主要有叶子节点 和 分支结点两种。
树中的结点是由一个数据元素 及若干指向其子树的分支组成的。一个结点拥有的子树数被称为是结点的度（Degree）。其中度为0的结点称为叶子节点（Leaf）或终端结点；而度不为0的结点称为非终端结点或分支结点。除根节点外，分支结点也称为内部结点。一棵树的度则是树内每个结点 度的最大值。
如上图所示：A的度为2，树内结点的度最大是D的3，所以这棵以A为root的树的度为3。

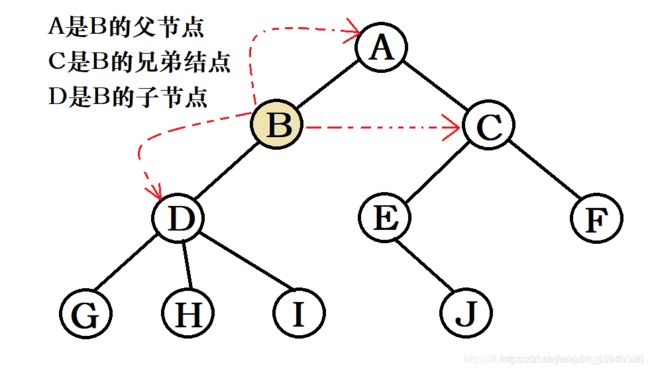
一个结点的子树的根称为该结点的孩子结点（child），通常我们称其为子结点；对应的，该结点称为孩子的双亲（parent），通常我们称为父节点。如上图所示：A就是其第一棵子树 的根B的父节点，C是A的孩子结点。

同一个双亲的孩子之间互称为兄弟（Sibling），例如B和C 。结点的祖先是从根到该结点所经分支上的所有结点，例如：G的祖先就是D B A。 反之，以某结点为根的子树中的任一结点都统称为该结点的子孙，例如：C的子孙节点有E J F。

结点的层次（Level）是从根开始定义的，根为第一层，根的孩子为第二层。若某结点在第 i 层，那么其子树的根就在第 i+1 层。如下图所示：A和B的关系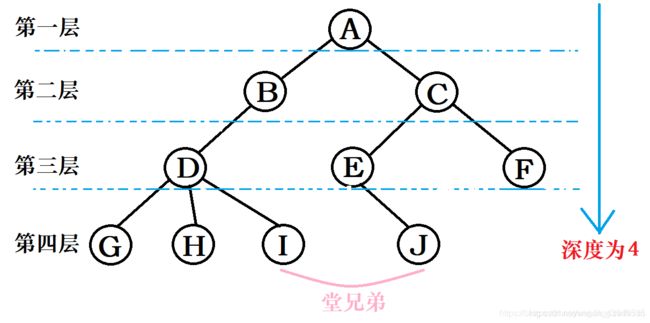

树的性质：

如上图所示：

1. 结点数=所有结点的度数+1；10=2+1+2+3+1 +1
2. 度为m的树中第i层上最多有m^(i-1)个结点；
3. 高度为h的m叉树中最多有(m^h-1)/(m-1)个结点；
4. 具有n个结点的m叉树的最小高度为{log m[n*(m-1)+1]}向上取整。
5. 总结点数=N0+N1+N2+…….Nm。同1
6. 总分支数=1xN1+2xN2+……+mxNm(度为m的结点引出m条分支)
7. 总结点数=总分支数+1

树的存储结构

对于树状结构：树的存储，仅仅使用顺序存储是不能满足树的实现，而且是需要结合顺序存储和链式存储来实现。通常表示一棵树的方法主要有顺序存储结构（双亲表示法）和链式存储结构（孩子表示法、孩子兄弟表示法）。请详见我的博客树的存储结构。

2019年9月8日18:43:57
接下来进入我们的重中之重：

二叉树

二叉树定义

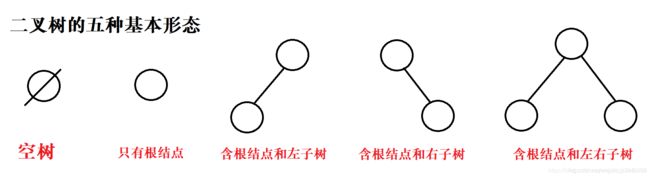
二叉树（Binary Tree）是由n（n≥0）个结点组成的有限集合，该集合为空集时（称为空二叉树）。或者由一个根结点以及两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。每个根结点只有两个子结点的就叫做二叉树。

二叉树作为树的一种特例，还需要满足在一般的树上加两个限制条件:

1. 二叉树中结点的度只能为0,1,2
2. 子树中有左右顺序之分，不能颠倒

典型的二叉树如下：

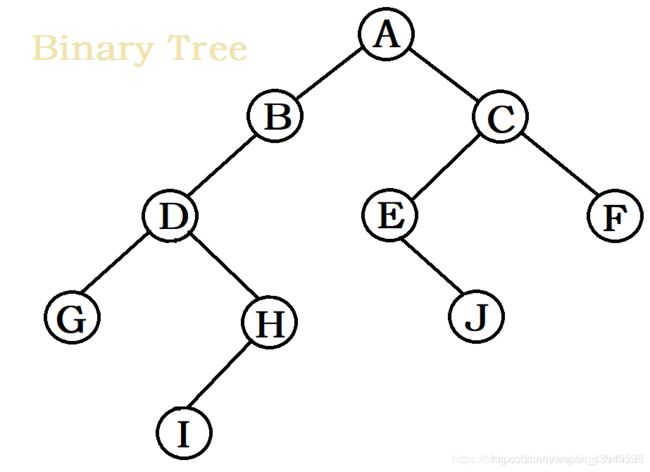
注：二叉树和度为2的树，绝不可以混为一谈。度为2的树至少有3个结点，而二叉树可以为空树。此外，度为2的有序树的孩子结点的左右次序是相对于另一孩子结点而言的，如果某个结点只有一个孩子结点，这个孩子结点就无须区分其左右次序，而二叉树无论其孩子数是否为2均需明确地确定其左右次序，也就是说二叉树的结点次序不是相对于另一结点而言，而是确定的。

二叉树的五种基本形态：

二叉树的特性

1. 每个结点最多有两棵子树，所以二叉树中不存在度大于 2 的结点。注意不是只有两棵子树，而是最多只能有。当然，没有子树或者只有一棵子树也都是可以的。
2. 左子树和右子树是有顺序的，次序不能任意颠倒。即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
3. 非空二叉树上叶子结点数等于度为2的结点数加1，即N0=N2+1
4. 非空二叉树第i层上至多有2^(i-1)个结点（i>=1）
5. 深度为 k的二叉树至多有 2^k-1个结点（k ≥ 1）
6. 高度为h的二叉树至多有2^h-1个结点（h>=1）

特殊的二叉树

单支树

单支树：也可以称作是斜树。即：所有的节点都只有左子树的二叉树叫左斜树；所有节点都只有右子树的二叉树叫右斜树。单支树非常明显的特点就是每一层只有一个节点，且节点的个数与二叉树的深度相同。其实线性结构可以理解为树的一种极其特殊的形式。单支树如下所示：

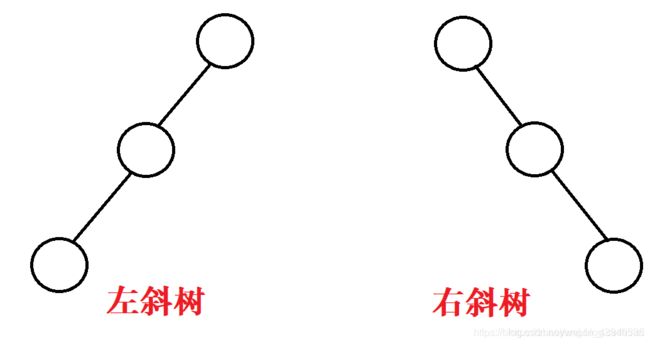
完全二叉树

如果对一棵具有着 n个节点的二叉树，按照层序进行编号，如果编号为 i（1=< i <=n ）的节点与同样深度的满二叉树中编号为 i 的节点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。完全二叉树如下图所示：

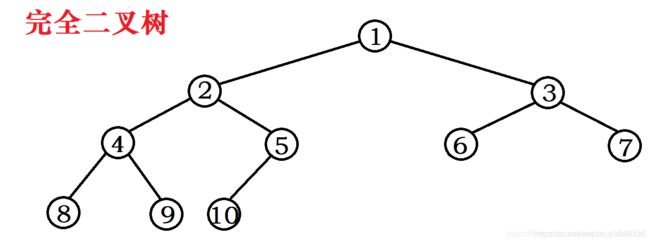
根据完全二叉树的定义：把完全二叉树的节点与同样深度的满二叉树各个节点进行编号比较，所有节点出现的位置相同，则是完全二叉树。所以，满二叉树一定是一棵完全二叉树，而完全二叉树不一定是满二叉树。

完全二叉树的特性如下：

1. 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
2. 如果有度为 1 的结点，那只可能有一个，且该节点只有左孩子，而无右孩子。
3. 如上图所示： 若i <=|_ n/2 _|（向下取整）,则结点i为分支结点，否则为叶子结点。
4. 叶子结点只可能在层次最大的两层的上出现。对于最大层次中的叶子结点，都依次排列在该层最左边的位置上。于是倒数第二层，若有叶子节点，一定都在右部连续位置。
5. 按层序编号后，一旦出现某结点（其编号为i）为叶子结点或只有左孩子，则编号大于i的结点均为叶子结点。（其实意思就是说：度为1的结点只可能出现在倒数第二层）。
6. 若n为奇数，则每个分支结点都有左孩子和右孩子；若n为偶数，则编号 最大的那个分支结点（n/2）只有左孩子，没有右孩子，其余分支结点左，右孩子都有。
7. 当i>1时，结点i的双亲编号为|_ i/2 _|（向下取整），即当i为偶数时，其双亲结点编号为 i/2,它是双亲结点的左孩子；当i为奇数时，其双亲结点编号为（i-1）/2 ,它是双亲结点的右孩子。
8. 当2i<=n时，结点i的左孩子编号为2i，否则无左孩子；2i+1<=n时，结点i的右孩子编号为2i+1，否则无右孩子。
9. 结点i所在层次（深度）为|_ log2i _|+1（向下取整）。
10. 具有n个（n>0）结点的一棵完全二叉树的高度为|- log 2 (n+1) -|(向上取整)或者是|_ log2 n_|+1（向下取整）。
11. 如果对一棵有 n个结点的完全二叉树（其深度为⌊log2n⌋+1 ）的结点按层序编号（从第1层到第 ⌊log2n⌋+1 层，每层从左到右），对任一结点 i（1≤i≤n）有：（1）如果 i=1，则结点 i是二叉树的根，无双亲；如果 i>1 ，则其双亲是结点 ⌊i/2⌋。（2）如果 2i>n ，则结点 i 无左孩子（结点 i为叶子结点）；否则其左孩子是结点 2i。（3）如果 2i+1>n，则结点 i无右孩子；否则其右孩子是结点 2i+1 。
12. 同样节点的二叉树，完全二叉树的深度最小。

满二叉树

满二叉树（是特殊的完全二叉树）：一颗高度为h，并且含有2*h-1个结点的二叉树称为满二叉树，即树中每一层都含有最多的结点。满二叉树如下图所示：

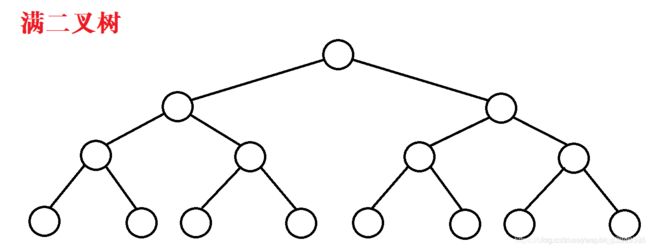
满二叉树的特性如下：

1. 所有分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上（最下层）。
2. 每个结点都存在左右子树，还得所有的叶子结点都在同一层上，这就做到了整棵树的平衡。
3. 非叶子节点的度一定是2。
4. 在同样深度的所有二叉树中，满二叉树的节点个数是最多的，叶子数最多的。
   

其他二叉树

1. 二叉排序树：在一棵二叉树上满足要求：

1. 若左子树不空，则左子树中所有关键字小于根关键字。
2. 若右子树不为空，则右子树中所有关键字都大于根关键字 。
3. 左、右子树各是一棵二叉排序树。

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。这就是我们通常所提到的BST树。BST树如下所示：

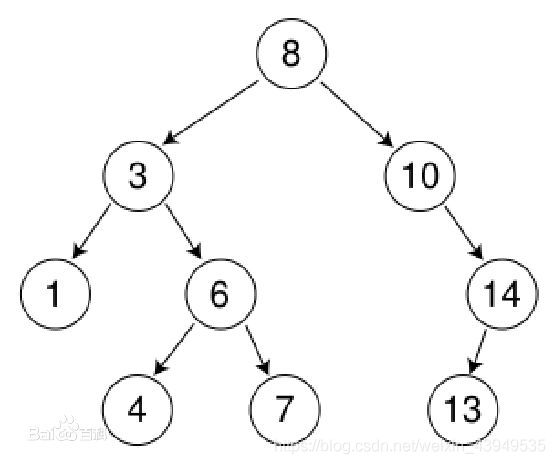
二叉排序树或者是一棵空树，或者是具有下列性质的二叉树。其定义如下：
（1）若左子树不空，则 左子树 上所有结点的值均 <= 它的 根结点 的值；
（2）若右子树不空，则 右子树 上所有结点的值均 >= 它的 根结点 的值；
（3）左、右子树也分别为二叉排序树 (递归定义)；

2. 平衡二叉树：特殊的二叉排序树，且左、右子树高度的绝对值不超过1。其定义如下：平衡二叉树（Self-balancing binary search tree），就是通常叫做AVL树的（这有别于AVL算法）。且具有以下性质：它是一 棵空树或它的 左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。所以说：平衡二叉树必定是二叉搜索树，反之则不一定。

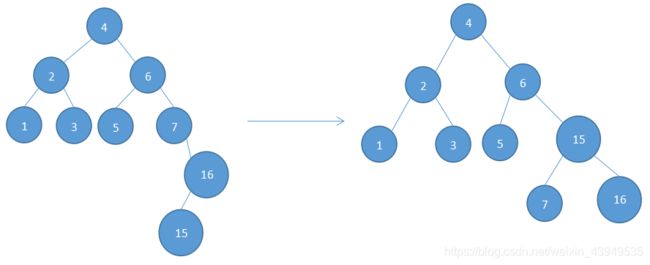
B树:一种平衡的多路查找树
线索二叉树：其目的是为了加快查找结点前驱和后继的速度。（通过利用n+1个空指针域）
以及RB树等。

注：2019年9月8日20:03:09 后面的高级数据结构非常重要，当然也是非常复杂的。近段时间，将会逐一进行详解更新。