时间窗和同时取送货的车辆路径问题(Vehicle Routing Problem with Simultaneous Piekup and Delivery and Time Windows,VRP

带时间窗和同时取送货的车辆路径问题(VehicleRouting Problem with Simultaneous Piekup and Delivery and Time Windows,VRPSPDTW)是指一组具有相同类型的车辆从配送中心出发,对其确定的客户集进行服务,完成服务后返回配送中心。每个客户的需求量和希望得到服务的时间窗是已知的,车辆在配送中心装好客户需要的货物在客户允许的时间窗内将货物送达,同时按取货要求从客手中将货物取回配送中心,每个客户仅由一辆车访问一次,问题是如何给每辆车确定其行驶路线,使车辆在行驶过程中满足车辆装载能力和行驶距离等限制条件下,以最少的车辆数、最低的行驶成本满足所有的客户需求。其示意图如下图所示：

VRPSPDTW是在VRPTW基础上加上取送货作业，按照取送货时各客户点间的关系可细分为多种类型,如取货作业一定要在所有送货作收完成后才能进行——即先送后取；各个客户点在进行送货服务的时候又可以顺便完成取货任务，但有可能在该客户点取到的货物将送到另一个客户点，即前点取后点送；各个客户点可以在取货的同时也送货,但是取到的货物带回配送中心，即同时取送。本文研究的问题类型属于同时取送型,车辆装载客户所需要的货物从配送中心出发，沿途进行送货，同时逐个取回客户所提供的货物，所有取回的货物都由车辆带回配送中心，每个客户仅能访问一次且必须访问一次。此外，在添加了时间窗约束的情况下，又可以根据客户对时间要求的严格程度，把VRPSPDTW分为带硬时间窗和同时取送货的车辆路径问题(VRPSPDHTW)和带软时间窗和同时取送货的车辆路径问题(VRPSPDSTW)，本文主要研究后一种情况,即在访问客户时允许偏离时间窗,但必须给予相应的惩罚,并以最小的时间窗偏离作为优化目标之一。此外，假设配送的物品都是性质相容,可以一起装载运输。

2 VRPSPDSTW数学模型

变量解释：

3 求解VRPSPDTW的遗传算法设计

尽管遗传算法可用于处理大规模、复杂的优化问题，但是其基本工作机理还是较为简单的，应用遗传算法进行求解的基本步骤如下:

(1) 确定有效且通用的编码方法，将问题的解直接或间接转化为有限位字符串。

(2) 随机产生一组问题的可行解构成初始种群,并进行参数设置。

(3) 计算种群中每个个体的适应度。

(4) 根据个体适应度的大小对种群以一定的概率执行选择、交叉、变异操作。

(5) 得到新一代种群,若满足终比条件,则将种群中的最大适应度值的个体作为最优解输出。否则返回步骤(3)。

算法流程如下图所示：

4 部分程序

%     Author:    怡宝2号          博士猿工作室

%     淘宝链接： https://shop437222340.taobao.com/index.htm?spm=2013.1.w5002-16262391244.6.733e1fb4LF2f58

 

%     Use:       用遗传求解解决同时取送货的冷链运输车辆路径问题；

%                坐标视自己的具体情况而定。

%     Illustrate:输入变量（must）：

%                                initial:客户的坐标信息

%                               initial.coordinate：要求的相应点的坐标，第一行是点的横坐标，第二行是点的纵坐标

%                                initial.demand（1*n），n表示工厂的个数；t表示各个工厂要求运送的货物的重量

%                                parameter.carload:每辆车限制的载重量

%

%                                parameter：各种成本的参数

%

%       Can—changed parameter：

%                                Option：遗传算法的相关参数

%                                Option.NIND：蚁群的规模

%                                Option.MAXGEN：蚁群的最大迭代代数

%                              

%                  输出：       bestpop：最短路程对应的路径

%                                trace ：最短路程

%         remark：如有疑问请咨询qq：778961303（paid help）

 

clc

clear all

close all

 

format compact

 

%遗传算法参数:NIND/种群规模；MAXGEN/最大迭代代数；PC/交叉概率；PM/变异概率；GGAP/遗传代沟

Option = struct('NIND',40, 'MAXGEN',200, 'PC', 0.85, 'PM', 0.1, 'GGAP', 0.8);

Option.w1 = 0.2; Option.w2 = 0.2; Option.w3 = 0.2; Option.w4 =0.2; Option.w5 = 0.2;            %多目标时每个目标函数的比重

 

%导入数据

[initial, parameter] = initialFunc();

 

%初始化种群

numclient = size(initial.coordinate,1);     %客户数包含配送中心

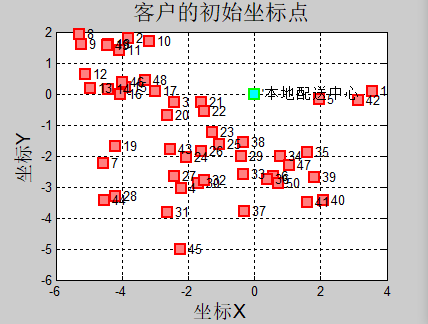
%  画出各客户的初始坐标

figure();

Initial_Draw( initial.coordinate,[1:1:numclient] );

 

%结果记录的结构体

Result = struct('mintrace',zeros( Option.MAXGEN,1),'bestpop',[]);

trace =Result;

 

%迭代开始

gen = 1;

whilegen<=Option.MAXGEN

       

    %计算目标函数

    [cost,fitness, fit] =CalculateFitness( Tabu, initial, parameter, Option);

   

    %选择

    [selch] =Select(chrom,fitness, Option.GGAP);

   

    %顺序交叉

    [selch] =CrossOver(selch, Option.PC);

   

    %交换变异

    selch =ExchangeMutation(selch);

       

    %计算目标函数和适应度

    [selcost, selfitness,selfit] = CalculateFitness( Tabu, initial, parameter, Option);

       

    %结果记录

    [mincost,index] =min(cost);

    trace.mintrace(gen) =min(cost);

    trace.bestpop(gen,:) =chrom(index(1),:);

   

    disp(['共迭代',num2str( Option.MAXGEN ),'次,现在为：',num2str(gen)]);

    gen = gen + 1;

end

 

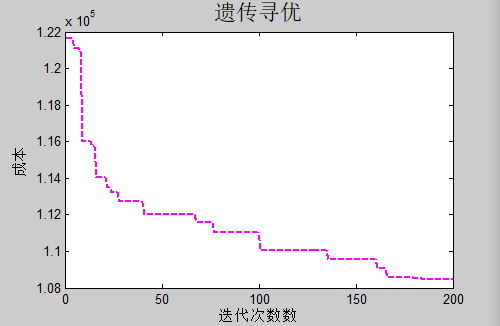
%绘制寻优迭代图

figure()

plot(trace.mintrace,'--m',...

    'LineWidth',2);

grid off

xlabel('迭代次数数')

ylabel('成本')

title('遗传寻优','fontsize',16)

 

%显示路径

[mintrace index] = min(trace.mintrace);              %最小成本

temp = trace.bestpop(index,:);                       %最小成本的

route = route( route',num2str(route(i))];

end

display(['求解的最优路径为：',num2str(p)]);

display(['0代表物流中心']);

disp(['最小的成本代价为：',num2str(min(trace.mintrace))]);

 

%画出路线图

figure();

% DrawRoute(initial.coordinate,route+1);

PlotRoute(route+1, initial.coordinate);

5 实验结果

6 参考文献

参考文献

[1] 关丽霞. 带软时间窗和同时取送货的车辆路径问题研究[D]. 中南大学, 2010. 64.

[2] 刘晴. 随机需求同时取送货车辆路径问题建模及优化研究[D]. 南京航空航天大学, 2012. 52.

[3] 同时取送货车辆路径问题的改进的蚁群算法_姚锦宝[Z].