AC自动机 进阶练习 (结合算法:矩阵快速幂/DP/高精度)
POJ 2778 DNA Sequence
题意:给你 n n n个病毒的DNA序列,现在要造出一个长度为 m m m的DNA序列,问你有多少种不含病毒DNA序列的方案。
首先可以看到要构造的序列长度很大,达到了2e9(20亿),遍历一遍都会超时,肯定得写一个时间复杂度在 O ( l o g n ) O(logn) O(logn)以下的算法。
怎么解决这一问题呢?先直接说结论吧:
用AC自动机构造出邻接矩阵,然后跑矩阵快速幂,最后取矩阵第0行元素之和即可。
看了这句话是不是一头雾水?(我也一样) 下面来分析一下为什么要构造邻接矩阵。
在离散数学中有这样一个结论:
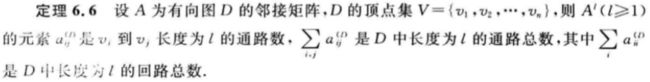
说人话 就是:从 u u u点到 v v v点恰好经过 k k k步的方案数,为邻接矩阵的 k k k次幂得到的矩阵(假设是 a n s ans ans)中的元素 a n s [ u ] [ v ] ans[u][v] ans[u][v]。(具体解法详见这篇文章)
那么这一结论对本题有什么启示呢?
所谓构造一个序列,其实就是让一个点从根节点开始走,保证走到的第一个点是序列的第一个元素,第二个点是第二个元素,走的过程实际上就是在Trie图中进行状态的转移。先看看暴力的想法:直接让一个点从根节点出发,在Trie图中“随便乱走”,由于Trie图在Trie树的基础上补全了不存在的出边节点, 那么每个点在下一步都有四个点(A,T,C,G)的选择,走到m步就停止,当然走的过程中不能经过病毒串终点,这样就是合法的序列。但是之前已经说过,不可能走m步,因为m太大了。
一次性走m步求不出,但是可以求每个点只走一步能转移到哪些点,这实际上就是求邻接矩阵。
如果我们能求出邻接矩阵 A A A,那么再求出 A m A^m Am,就得到了走m步能到达的点的所有情况。在 A m A^m Am矩阵中,第0行,第 j 列元素表示从0点开始走m步走到 j 点可能的方案数,求和即可。
注意ac自动机中的cnt[]成为病毒串标记,在构造fail指针时记得将标记向下传递。
AC代码:
#include HDU 2243 考研路茫茫——单词情结
和上题差不多,这个是要求<=m的所有方案,构造一个矩阵[{E,E},{0,A}]进行快速幂即可得到A0+A1+…+Am。
然后对264取模的意思就是定义成unsigned long long,计算过程中会自动对264取模 (我先还以为是大数取模呢)
#include POJ 1625 Censored!
这题需要用到高精度,然后因为幂次比较小可以不用快速幂,直接DP就行,我想着java有大数,那就拿java写一下大数的矩阵快速幂吧。
注意编码格式,因为java没有unsigned char。将输入写成Scanner cin = new Scanner(new BufferedInputStream(System.in), "ISO-8859-1"); 即可。
Java代码:
//package Main; //package信息一定要去掉,否则RE
import java.io.BufferedInputStream;
import java.math.BigInteger;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
class Matrix {
BigInteger m[][];
Matrix(int sz, int type) { // type控制零矩阵/单位矩阵
m = new BigInteger[sz][sz];
for(int i = 0; i < sz; i++)
for(int j = 0; j < sz; j++)
m[i][j] = BigInteger.ZERO;
if(type == 1) {
for(int i = 0; i < sz; i++)
m[i][i] = BigInteger.ONE;
}
}
}
class Trie {
static final int N = 105, M = 55, K = 256;
int ch[][] = new int[N][M];
int fail[] = new int[N];
boolean cnt[] = new boolean[N];
int tot = 0;
int len;
Queue<Integer> q = new LinkedList<Integer>();
int mp[] = new int[K];
void ins(String s) {
int u = 0;
for(int i = 0; i < s.length(); i++)
{
int x=mp[s.charAt(i)]; // ASCII码 -> 0~len-1(len是字母表长度)
if(ch[u][x] == 0) ch[u][x] = ++tot;
u = ch[u][x];
}
cnt[u] = true;
}
void build_fail() {
for(int i = 0; i < len; i++) {
if(ch[0][i] != 0)
q.offer(ch[0][i]);
}
while(!q.isEmpty()) { // 队列非空
int u = q.poll(); // 取出并删除队头的元素
for(int i = 0; i < len; i++) {
int v = ch[u][i];
int f = ch[fail[u]][i];
if(v != 0) {
if(cnt[f] == true) cnt[v] = true;
fail[v] = f;
q.offer(v);
}
else ch[u][i] = f;
}
}
}
Matrix build_matrix() {
int sz = tot + 1;
Matrix ans = new Matrix(sz, 0);
for(int i = 0; i < sz; i++) {
if(cnt[i]) continue;
for(int j = 0;j < len; j++) {
int v = ch[i][j];
if(!cnt[v])
ans.m[i][v] = ans.m[i][v].add(BigInteger.ONE);
}
}
return ans;
}
Matrix mul(Matrix s1, Matrix s2) {
int sz = tot + 1;
Matrix ans = new Matrix(sz, 0);
for(int i = 0; i < sz; i++)
for(int j = 0; j < sz; j++)
for(int k = 0; k < sz; k++)
ans.m[i][j] = ans.m[i][j].add(s1.m[i][k].multiply(s2.m[k][j]));
return ans;
}
Matrix matrix_pow(Matrix a, int b) {
int sz = tot + 1;
Matrix ans = new Matrix(sz, 1);
while(b != 0) {
if(b%2 == 1) ans = mul(ans,a);
a = mul(a,a);
b /= 2;
}
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner(new BufferedInputStream(System.in), "ISO-8859-1");
//Scanner cin = new Scanner(System.in); 会RE
Trie ac = new Trie();
ac.len = cin.nextInt();
int m = cin.nextInt();
int n = cin.nextInt();
String s = cin.next();
for(int i = 0; i < ac.len; i++) {
ac.mp[s.charAt(i)] = i;
}
for(int i = 1; i <= n; i++) {
String t = cin.next(); // 病毒串
ac.ins(t);
}
ac.build_fail();
Matrix a = ac.build_matrix(); // 邻接矩阵
Matrix ans = ac.matrix_pow(a,m);
BigInteger sum = BigInteger.ZERO;
int sz = ac.tot + 1;
for(int i = 0; i < sz; i++) {
sum = sum.add(ans.m[0][i]);
}
System.out.println(sum);
}
}
C++代码(没写大数,不能AC,只是作为java代码的“翻译”):
#include