ICPC Yokohama 2019 训练赛

A-FastForwarding

Mr. Anderson frequently rents video tapes of his favorite classic films. Watching the films so many times, he has learned the precise start times of his favorite scenes in all such films. He now wants to find how to wind the tape to watch his favorite scene as quickly as possible on his video player.

When the [play] button is pressed, the film starts at the normal playback speed. The video player has two buttons to control the playback speed: The [3x] button triples the speed, while the [1/3x] button reduces the speed to one third. These speed control buttons, however, do not take effect on the instance they are pressed. Exactly one second after playback starts and every second thereafter, the states of these speed control buttons are checked. If the [3x] button is pressed on the timing of the check, the playback speed becomes three times the current speed. If the [1/3x] button is pressed, the playback speed becomes one third of the current speed, unless it is already the normal speed.

For instance, assume that his favorite scene starts at 19 seconds from the start of the film. When the [3x] button is on at one second and at two seconds after the playback starts, and the [1/3x] button is on at three seconds and at five seconds after the start, the desired scene can be watched in the normal speed five seconds after starting the playback, as depicted in the following chart.

Your task is to compute the shortest possible time period after the playback starts untilthe desired scene starts. The playback of the scene, of course,should be in the normal speed.
Input
The inputconsists of a single test case of the following format.
tt
The given single integer t (0 ≤ t< 2^{50})t(0≤t<2
50
) is the start time of the target scene.
Output
Print an integer that is the minimumpossible time in seconds before he can start watching the target scene in thenormal speed.

样例输入1复制
19
样例输出1复制
5
样例输入2复制
13
样例输出2复制
5
样例输入3复制
123456789098765
样例输出3复制
85

题目分析：
最高能允许提高到多少倍速（保证能降下来的前提下），这个最gap倍速是可以算出来的， 然后算一下那些剩余的时间就好了 对于剩余的时间也是尽量有高德倍速去播放

#include 
#include 
#include 
#include 
#define LL long long
using namespace std;
int main() {
    LL tt,t; cin >> t;
    if(t <= 3) { cout << t; return 0; }
    t -= 1;
    LL sum = 0,pre = 3,now,Ans = 2,peace = 3;
    while(1) {
        sum = pre + peace * 3 + peace;
        if(sum <= t) { pre = sum; peace *= 3; Ans += 2; }
        else break;
    }
    LL last = t - pre;
    while(peace >= 1 && last > 0) {
        Ans += (last / peace);
        last %= peace;
        peace /= 3;
    }
    //Ans += (last / peace);
    cout << Ans << endl;
    return 0;
}

B-Estimating the Flood Risk

Mr. Boat is the owner of a vast extent of land. As many typhoons have struck Japan this year, he became concerned of flood risk of his estate and he wants to know the average altitude of his land. The land is too vast to measure the altitude at many spots. As no steep slopes are in the estate, he thought that it would be enough to measure the altitudes at only a limited number of sites and then approximate the altitudes of the rest based on them.

Multiple approximations might be possible based on the same measurement results, in which case he wants to know the worst case, that is, one giving the lowest average altitude.
Mr. Boat’s estate, which has a rectangular shape, is divided into grid-aligned rectangular areas of the same size. Altitude measurements have been carried out in some of these areas, and the measurement results are now at hand. The altitudes of the remaining areas are to be approximated on the assumption that altitudes of two adjoining areas sharing an edge differ at most 1.
In the first sample given below, the land is divided into 5 × 4 areas. The altitudes of the areas at (1, 1) and (5, 4) are measured 10 and 3, respectively. In this case, the altitudes of all the areas are uniquely determined on the assumption that altitudes of adjoining areas differ at most 1.
In the second sample, there are multiple possibilities, among which one that gives the lowest average altitude should be considered.
In the third sample, no altitude assignments satisfy the assumption on altitude differences.

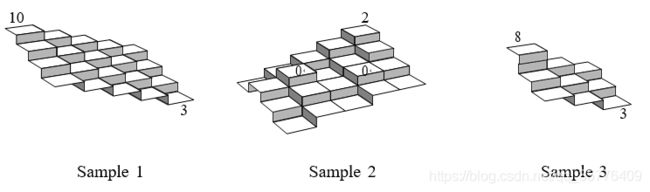
Your job is to write a program that approximates the average altitude of his estate. To be precise, the program should compute the total of approximated and measured altitudes of all the mesh-divided areas. If two or more different approximations are possible, the program should compute the total with the severest approximation, that is, one giving the lowest total of the altitudes.

Output

If all the unmeasured areas can be assigned their altitudes without any conflicts with the mea- sured altitudes assuming that two adjoining areas have the altitude difference of at most 1, output an integer that is the totaltotal of the measured or approximated altitudes of all the areas. If more than one such altitude assignment is possible, output the minimum altitude total among the possible assignments.If no altitude assignments satisfy the altitude difference assumption, output No.

样例输入1复制
5 4 2
1 1 10
5 4 3
样例输出1复制
130
样例输入2复制
5 4 3
2 2 0
4 3 0
5 1 2
样例输出2复制
-14
样例输入3复制
3 3 2
1 1 8
3 3 3
样例输出3复制
No

题目分析：
总的平均海拔最小也就是要求每个地方的海拔尽可能小，最大值最小—>二分答案？？？？？？？？ 好像显然不合适

#include 
#include 
#include 
#include 
using namespace std;
#define Maxn  55
int h[Maxn][Maxn];// 每个位置最小的海拔   同时每个位置最高的海拔应尽可能小 以保证平均数的尽可能小
int x[Maxn],y[Maxn],high[Maxn];
// 相邻位置 最多相差高度1    那么高度只差最多为曼哈顿距离
//所以这个点根据第i组数据确定的海拔为  hi - d , hi + d  d表示曼哈顿距离
//尽可能取hi - d
int main() {
    int w,d, n; scanf("%d %d %d",&w,&d,&n);
    for(int i=1; i<=n; i++)
        scanf("%d %d %d",&x[i],&y[i],&high[i]);
    int flag = 0;
    for(int i=1; i<=n; i++)
        for(int j=1; j<i; j++) {
            if( abs(high[i] - high[j]) > abs(x[i] - x[j]) + abs(y[i] - y[j])) { flag = 1; break; }
        }
    if(flag) { cout << "No" << endl; return 0; }

    for(int i=0; i<Maxn; i++)
        for(int j=0; j<Maxn; j++) h[i][j] = -1e9;

    for(int i=1; i<=n; i++)
        for(int j=1; j<=w; j++)
            for(int k=1; k<=d; k++)
                h[j][k] = max(h[j][k],high[i] - (abs(j - x[i]) + abs(k - y[i])));

    long long Ans = 0;
    for(int i=1; i<=w; i++)
        for(int j=1; j<=d; j++)
            Ans += h[i][j];
        cout << Ans << endl;
    return 0;
}