NOIP2016提高组Day1 真题测试
T1:玩具谜题
题目描述
小南有一套可爱的玩具小人,它们各有不同的职业。
有一天,这些玩具小人把小南的眼镜藏了起来。小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
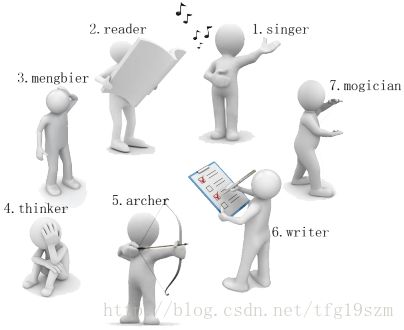
这时 singer 告诉小南一个谜题:“眼镜藏在我左数第 3 个玩具小人的右数第 1 个玩具小人的左数第 2 个玩具小人那里。”
小南发现,这个谜题中玩具小人的朝向非常关键,因为朝内和朝外的玩具小人的左右方向是相反的:面朝圈内的玩具小人,它的左边是顺时针方向,右边是逆时针方向;而面向圈外的玩具小人,它的左边是逆时针方向,右边是顺时针方向。
小南一边艰难地辨认着玩具小人,一边数着:
“singer 朝内,左数第 3 个是 archer。
“archer 朝外,右数第 1 个是 thinker。
“thinker 朝外,左数第 2 个是 writer。
“所以眼镜藏在 writer 这里!”
虽然成功找回了眼镜,但小南并没有放心。如果下次有更多的玩具小人藏他的眼镜,或是谜题的长度更长,他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。这样的谜题具体可以描述为:
有 n 个玩具小人围成一圈,已知它们的职业和朝向。现在第 1 个玩具小人告诉小南一个包含 m 条指令的谜题,其中第 i 条指令形如“左数/右数第 si 个玩具小人”。你需要输出依次数完这些指令后,到达的玩具小人的职业。
输入格式
输入的第一行包含两个正整数 n ,m ,表示玩具小人的个数和指令的条数。
接下来 n 行,每行包含一个整数和一个字符串,以逆时针为顺序给出每个玩具小人的朝向和职业。其中 0 表示朝向圈内,1 表示朝向圈外。保证不会出现其他的数。字符串长度不超过 10 且仅由小写字母构成,字符串不为空,并且字符串两两不同。整数和字符串之间用一个空格隔开。
接下来 m 行,其中第 i 行包含两个整数 ai,si ,表示第 i 条指令。若 ai = 0 ,表示向 左数 si 个人;若 ai = 1 ,表示向右数 si 个人。保证 ai 不会出现其它的数,1 ≤si <n。
输出格式
输出一个字符串,表示从第一个读入的小人开始,依次数完 m 条指令后到达的小人的职业。
样例数据 1
输入
7 3
0 singer
0 reader
0 mengbier
1 thinker
1 archer
0 writer
1 mogician
0 3
1 1
0 2
输出
writer
样例数据 2
输入
10 10
1 c
0 r
0 p
1 d
1 e
1 m
1 t
1 y
1 u
0 v
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4
输出
y
备注
【样例1说明】
这组数据就是【题目描述】中提到的例子。
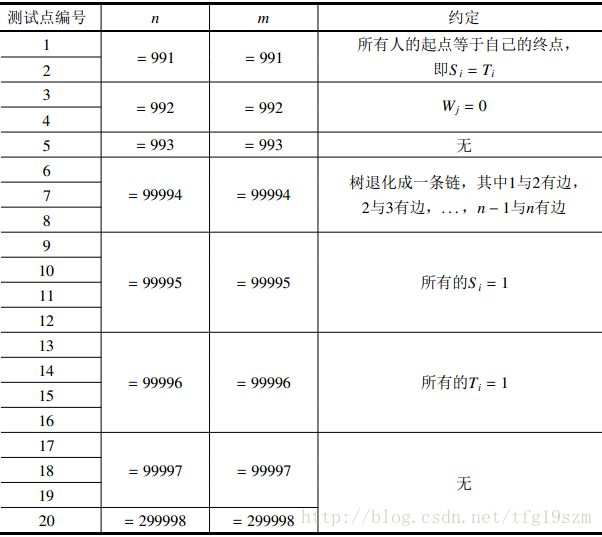
其中一些简写的列意义如下:
全朝内:若为“√”,表示该测试点保证所有的玩具小人都朝向圈内;
全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 1≤i≤m ,ai = 0 ;
si = 1 :若为“√”,表示该测试点保证所有的指令都只数 1 个,即对任意的 1≤i≤m , si = 1 ;
职业长度为 1 :若为“√”,表示该测试点保证所有玩具小人的职业一定是一个 长度为 1 的字符串。
T1题解:
【算法分析】
简单模拟。
【代码】
#includecin>>num[i].turn>>num[i].name;
for(int i=0;ilong long x,y;
cin>>x>>y;
work(x,y);
}
cout<return 0;
} T2:天天爱跑步
题目描述
小 C 同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 n 个结点和 n-1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 1 到 n 的连续正整数。
现在有 m 个玩家,第 i 个玩家的起点为 Si ,终点为 Ti 。每天打卡任务开始时,所有玩家在第 0 秒同时从自己的起点出发,以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小 C 想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点 j 的观察员会选择在第 Wj 秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第 Wj 秒也正好到达了结点 j 。 小 C 想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一段时间后再被观察员观察到。 即对于把结点 j 作为终点的玩家: 若他在第 Wj 秒前到达终点,则在结点 j 的观察员不能观察到该玩家;若他正好在第 Wj 秒到达终点,则在结点 j 的观察员可以观察到这个玩家。
输入格式
第一行有两个整数 n 和 m 。其中 n 代表树的结点数量, 同时也是观察员的数量, m 代表玩家的数量。
接下来 n-1 行每行两个整数 u 和 v ,表示结点 u 到结点 v 有一条边。
接下来一行 n 个整数,其中第 j 个整数为 Wj, 表示结点 j 出现观察员的时间。
接下来 m 行,每行两个整数 Si 和 Ti ,表示一个玩家的起点和终点。
对于所有的数据,保证 1≤Si,Ti≤n,0≤Wj≤n 。
输出格式
输出 1 行 n 个整数,第 j 个整数表示结点 j 的观察员可以观察到多少人。
样例数据 1
输入
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
输出
2 0 0 1 1 1
样例数据 2
输入
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
输出
1 2 1 0 1
备注
【样例1说明】
对于 1 号点,W1 = 0 ,故只有起点为 1 号点的玩家才会被观察到,所以玩家 1 和玩家 2 被观察到,共有 2 人被观察到。
对于 2 号点,没有玩家在第 2 秒时在此结点,共 0 人被观察到。
对于 3 号点,没有玩家在第 5 秒时在此结点,共 0 人被观察到。
对于 4 号点,玩家 1 被观察到,共 1 人被观察到。
对于 5 号点,玩家 1 被观察到,共 1 人被观察到。
对于 6 号点,玩家 3 被观察到,共 1 人被观察到。
【提示】
如果你的程序需要用到较大的栈空间(这通常意味着需要较深层数的递归),请务必仔细阅读选手目录下的文档“running/stack.pdf”,以了解在最终评测时栈空间的限制与在当前工作环境下调整栈空间限制的方法。
附:running/stack.pdf 文件内容
在最终评测时,调用栈占用的空间大小不会有单独的限制,但在我们的工作环境中默认会有 8 MB 的限制。这可能会引起函数调用层数较多时,程序发生栈溢出崩溃。
我们可以使用一些方法修改调用栈的大小限制。例如,在终端中输入下列命令:
ulimit -s 1048576
此命令的意义是,将调用栈的大小限制修改为 1 GB。
例如,在选手目录建立如下sample.cpp 或 sample.pas

将上述源代码编译为可执行文件 sample 后,可以在终端中运行如下命令运行该程序
./sample
如果在没有使用命令“ulimit -s 1048576”的情况下运行该程序,sample 会因为栈溢出而崩溃;如果使用了上述命令后运行该程序,该程序则不会崩溃。
特别地,当你打开多个终端时,它们并不会共享该命令,你需要分别对它们运行该命令。
请注意,调用栈占用的空间会计入总空间占用中,和程序其他部分占用的内存共同受到内存限制。
T2题解:
【算法分析】
我们思考一下从x到y的路径,这个可以拆成从x到lca的路径和从lca到y的路径,
这个很明显。
如 果 一 个 点i 在从x 到lca 的 路 径 可 以 检 测 到 的 话 , 那 么 就 有
deep[i]+w[i]=deep[x]。
如 果 一 个 点i 在从lca 到y 的 路 径 上 可 以 检 测 到 的 话 , 那 么 就 有
deep[i]-w[i]=deep[y]-t(t表示x到y的路径长度)。
对于每个点i,我们已知deep[i],w[i],只需要在路径上标上等号左侧的数字。
考虑树上差分,将问题转化为子树集。
dfs维护两个桶,一个向上的桶a和一个向下的桶b(分别表示deep[x],deep[y]-t)。
每次ans[x]的答案就是子树a[deep[x]+w[x]]+b[deep[x]-w[x]]的数量。
答案用进入该节点时候的值减去出节点即可。
【代码】
#includeint k=deep[a]-deep[b];
for(int i=18;i>=-1;--i)
if(k&(1<if(a==b)
return a;
for(int i=18;i>=-1;--i)
if(jump[a][i]!=jump[b][i])
{
a=jump[a][i];
b=jump[b][i];
}
return jump[a][0];
}
inline void work(int x)
{
int last=num[deep[x]+w[x]]+num[w[x]-deep[x]+n*3+1];
int k=point[x].size();
for(int i=0;ifor(int i=first[x];i;i=edge[i].next)
if(edge[i].to!=jump[x][0])
work(edge[i].to);
ans[x]=num[deep[x]+w[x]]+num[w[x]-deep[x]+n*3+1]-last;
}
int main()
{
int _q=20<<20;
char *_p=(char*)malloc(_q)+_q;
__asm__("movl %0, %%esp\n"::"r"(_p));
int i,j,k,s,t;
node2 u;
n=read();
m=read();
for(i=1;i<=n-1;++i)
{
s=read();
t=read();
add(s,t);
add(t,s);
}
DFS(1);
for(i=1;i<=n;++i)
w[i]=read();
for(i=1;i<=m;++i)
{
s=read();
t=read();
k=LCA(s,t);
u.s=deep[s];
u.t=1;
point[s].push_back(u);
u.t=-1;
point[jump[k][0]].push_back(u);
u.s=deep[s]-deep[k]*2+n*3+1;u.t=1;
point[t].push_back(u);
u.t=-1;
point[k].push_back(u);
}
work(1);
for(i=1;i<=n;++i)
cout<" ";
return 0;
} T3:换教室
题目描述
对于刚上大学的牛牛来说,他面临的第一个问题是如何根据实际情况申请合适的课程。
在可以选择的课程中,有 2n 节课程安排在 n 个时间段上。在第 i(1≤i≤n)个时间段上,两节内容相同的课程同时在不同的地点进行,其中,牛牛预先被安排在教室 ci 上课,而另一节课程在教室 di 进行。
在不提交任何申请的情况下,学生们需要按时间段的顺序依次完成所有的 n 节安排好的课程。如果学生想更换第 i 节课程的教室,则需要提出申请。若申请通过,学生就可以在第 i 个时间段去教室 di 上课,否则仍然在教室 ci 上课。
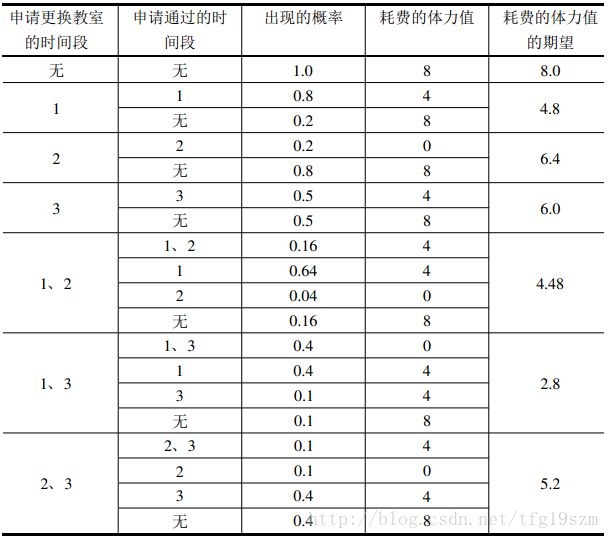
由于更换教室的需求太多,申请不一定能获得通过。通过计算,牛牛发现申请更换第 i 节课程的教室时,申请被通过的概率是一个已知的实数 ki ,并且对于不同课程的申请,被通过的概率是互相独立的。
学校规定,所有的申请只能在学期开始前一次性提交,并且每个人只能选择至多 m 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室,而不能根据某些课程的申请结果来决定其他课程是否申请;牛牛可以申请自己最希望更换教室的 m 门课程,也可以不用完这 m 个申请的机会,甚至可以一门课程都不申请。
因为不同的课程可能会被安排在不同的教室进行,所以牛牛需要利用课间时间从一间教室赶到另一间教室。
牛牛所在的大学有 v 个教室,有 e 条道路。每条道路连接两间教室,并且是可以双向通行的。由于道路的长度和拥堵程度不同,通过不同的道路耗费的体力可能会有所不同。当第 i(1≤i≤n-1)节课结束后,牛牛就会从这节课的教室出发,选择一条耗费体力最少的路径前往下一节课的教室。
现在牛牛想知道,申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小,请你帮他求出这个最小值。
输入格式
第一行四个整数 n,m,v,e 。n 表示这个学期内的时间段的数量;m 表示牛牛最多可以申请更换多少节课程的教室;v 表示牛牛学校里教室的数量;e 表示牛牛的学校里道路的数量。
第二行 n 个正整数,第 i(1≤i≤n)个正整数表示 ci ,即第 i 个时间段牛牛被安排上课的教室;保证 1≤ci≤v。
第三行 n 个正整数,第 i(1≤i≤n)个正整数表示 di ,即第 i 个时间段另一间上同样课程的教室;保证 1≤di≤v。
第四行 n 个实数,第 i(1≤i≤n)个实数表示 ki ,即牛牛申请在第 i 个时间段更换教室获得通过的概率。保证 0≤ki≤1。
接下来 e 行,每行三个正整数 aj ,bj ,wj ,表示有一条双向道路连接教室 aj ,bj ,通过这条道路需要耗费的体力值是 wj;保证 1≤aj,bj≤v,1≤wj≤100
保证 1≤n≤2000,0≤m≤2000,1≤v≤300,0≤e≤90000。
保证通过学校里的道路,从任何一间教室出发,都能到达其他所有的教室。
保证输入的实数最多包含 3 位小数。
输出格式
输出一行,包含一个实数,四舍五入精确到小数点后恰好 2 位,表示答案。你的输出必须和标准输出完全一样才算正确。
测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 4×10-3。(如果你不知道什么是浮点误差,这段话可以理解为:对于大多数的算法,你可以正常地使用浮点数类型而不用对它进行特殊的处理)
样例数据 1
输入
3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1
输出
2.80
【提示】
道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。
请注意区分 n,m,v,e 的意义,n 不是教室的数量,m 不是道路的数量。
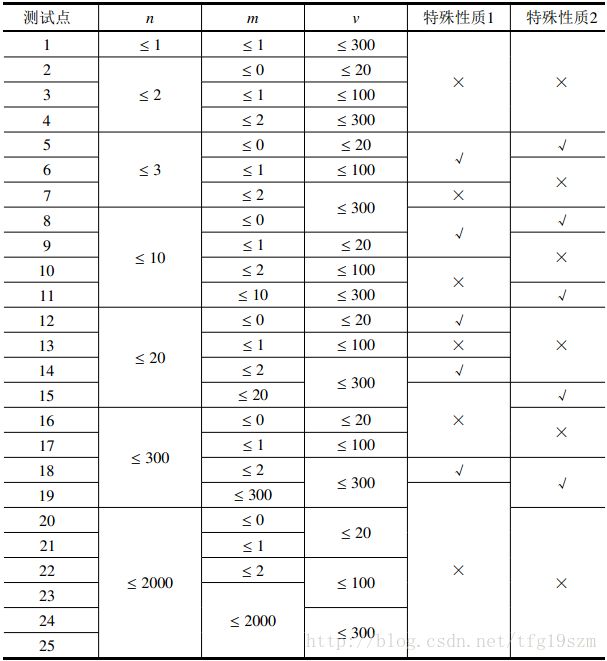
特殊性质1:图上任意两点 ai,bi,ai≠bi 间 ,存在一条耗费体力最少的路径只包含一条道路。
特殊性质2:对于所有的 1≤i≤n,ki=1。
T3题解:
【算法分析】
先用floyd预处理一下。
设f[i][j][k]表示第i个时间段,选了j个教室要申请(不一定成功),k表示i申请
或不申请。
我们从i推到i+1,如果要推到f[i+1][j][0]的话,那么第i+1个时间段肯定在a[i+1]。
这个可以从i的0状态和1状态推过来,如果从0推过来,那么i时间段肯定在a[i]这个
地方,那么期望是d[a[i]][a[i+1]],概率是1。如果从1推过来,那么i有两种情况,申
请成功和申请不成功,所以i时间段可能在a[i]或b[i],概率为1-gai[i]和gai[i]。
所以f[i+1][j][0]=min(f[i][j][0]+d[a[i]][a[i+1]],f[i][j][1]+(1−gai[i])∗
d[a[i]][a[i+1]]+gai[i]∗d[b[i]][a[i+1]]);
要推倒f[i+1][j][1]情况类似,不过要考虑i+1申请成不成功的情况。
f[i+1][j+1][1]=
min(f[i][j][0]+d[a[i]][b[i+1]]∗gai[i+1]+d[a[i]][a[i+1]]∗(1−
gai[i+1]),f[i][j][1]+d[a[i]][a[i+1]]∗(1−gai[i])∗(1−gai[i+1])+d[b[i]][a[i+1]]∗gai[i]∗(1−
gai[i+1])+d[a[i]][b[i+1]]∗(1−gai[i])∗gai[i+1]+d[b[i]][b[i+1]]∗gai[i]∗gai[i+1]);
最后答案就是min(f[n][j][0,1])
【代码】
#includefor(int j=0;j<=m;++j)
{
f[i+1][j][0]=min(f[i][j][1]+k[i]*dis[d[i]][c[i+1]]+(1.0-k[i])*dis[c[i]][c[i+1]],f[i][j][0]+dis[c[i]][c[i+1]]);
f[i+1][j+1][1]=min(f[i][j][1]+k[i]*k[i+1]*dis[d[i]][d[i+1]]+(1.0-k[i])*k[i+1]*dis[c[i]][d[i+1]]+k[i]*(1.0-k[i+1])*dis[d[i]][c[i+1]]+(1.0-k[i])*(1.0-k[i+1])*dis[c[i]][c[i+1]],f[i][j][0]+k[i+1]*dis[c[i]][d[i+1]]+(1.0-k[i+1])*dis[c[i]][c[i+1]]);
}
}
inline void giveout()
{
for(int i=0;i<=m;++i)
ans=min(ans,min(f[n][i][0],f[n][i][1]));
printf("%0.2f",ans);
}
int main()
{
cin>>n>>m>>v>>e;
getin();
FL();
DP();
giveout();
return 0;
} 2017年7月19日15:55:36