《Mastering the game of Go without human knowledge》译文
1. 摘要
人工智能的长期目标是后天自主学习,并且在一些具有挑战性的领域中实现超人的算法。最近,AlphaGo成为第一个在围棋中击败人类世界冠军的程序。AlphaGo的树搜索使用深度神经网络来评估棋局和选定下棋位置。神经网络是利用对人类专业棋手的移动进行监督学习,同时通过自我博弈进行强化学习来进行训练的。在这里,我们引入了一种没有人类的数据、指导或超越游戏规则的领域知识的、基于强化学习的算法。AlphaGo成为了自己的老师:神经网络被训练用来预测AlphaGo自己的落子选择和胜负。这种神经网络提高了树搜索的强度,从而提高了落子选择的质量和在下一次迭代中的自我博弈能力。从零开始,我们的新程序“AlphaGo Zero”取得了“超人”的成绩,以100比0战胜了的此前公布的AlphaGo版本(指代和李世石对弈的AlphaGo)。
2. 引言
使用监督学习系统来做出与人类棋手一样的决策使人工智能取得了很大进展。然而,人类棋手的数据集通常是昂贵的、不可靠的或根本不可用的。即使在可靠的数据集可用时,人类的认知局限也可能对以这种方式训练的系统的性能施加上限。相比之下,强化学习系统是通过自己的经验训练的,原则上他们能够超越人的能力,并在缺乏人类知识的领域中运作。近年来,利用强化学习训练的深层神经网络在这一目标上取得了快速的进展。这些系统在电脑游戏如Atari和3D虚拟环境上已经超过了人类。但是,在人类智力方面最具挑战性的领域,如围棋领域,使用完全通用的方法没有办法实现与人类相媲美的性能。因为围棋被广泛视为是人工智能的一大挑战——它需要在庞大的搜索空间上进行精确和复杂的前瞻。
AlphaGo是第一个在围棋比赛中实现超人表现的程序。之前发布的我们称之为AlphaGo Fan的版本,在2015年10月击败了欧洲冠军樊麾。AlphaGo Fan使用两个深层神经网络:一个是策略网络,来输出下一步落子的概率;另一个是价值网络,来输出对棋局的评估,也就是落子的胜率。策略网络最初是通过监督学习来精确预测人类专业棋手的落子,随后又通过策略梯度强化学习对系统进行了增强。价值网络通过使用策略网络进行自我博弈来预测谁是赢家从而完成训练。一旦经过训练,这些网络结合蒙特卡洛树搜索(MCTS)提供对未来局势的预测。运用策略网络来缩小高概率落子的搜索过程,运用价值网络结合蒙特卡洛快速走子策略来评估树中的落子位置。随后开发的版本,我们称之为AlphaGo Lee,用类似的方法,在2016年3月击败具有国际冠军头衔的Lee Sedol(曾获18项国际冠军)。
我们现在的程序AlphaGo Zero,与AlphaGo Fan和AlphaGo Lee存在以下几点的差异:
• 它完全由自我博弈强化学习进行训练,从刚开始的随机博弈开始,就没有任何监督或使用人类的数据
• 它只使用棋盘上的黑白棋作为输入特征
• 它使用单一的神经网络,而不是分离的策略网络和价值网络
• 它使用了一个简化版搜索树,这个搜索树依靠单一的神经网络进行棋局评价和落子采样,不执行任何蒙特卡洛rollout
为了实现上述结果,我们引入一个新的强化学习算法,在训练过程中完成前向搜索,从而达到迅速的提高以及精确、稳定的学习过程。
3. AlphaGo Zero的强化学习
我们在学习中使用一个参数为θ的深度神经网络fθ,该神经网络将棋局和其历史的原始图作为输入,输出落子概率和价值(p, v) = fθ(s)。落子概率向量p代表选择每个落子动作a(包括放弃行棋)的概率pa = Pr(a| s),价值v是标量评估,估计当前玩家在棋局状态为 s 时获胜的概率。这个神经网络将策略网络和价值网络合并成一个单一的体系结构。神经网络包括许多残差块、批量归一化和非线性修正其的卷积层。
AlphaGo Zero的神经网络是通过新的强化学习算法利用自我博弈训练出来的。在每一个棋局 s,通过神经网络fθ的指导来执行蒙特卡洛搜索。MCTS搜索输出每次落子的概率分布π。经过搜索后的落子概率 p 通常比神经网络 fθ(s) 输出的落子概率 p 更强,因此MCTS被看作是一个强大的策略改进算法。带有搜索的自我博弈——采用改进的以MCTS为基础的策略来选择的每一次落子,然后用游戏的赢家 z 作为价值的样本——可以被看作是一个强有力的策略评估运算符。我们采用的强化学习算法的主要思想是在策略迭代过程中反复地利用这些搜索算子,神经网络的参数被更新,使移动概率值(p,v) = fθ(s) 更紧密地与改进的搜索概率和自我博弈的赢家(π,z)相配;这些新的参数用于下一次的自我博弈迭代,以使搜索更强大。
图 1 a 这个程序进行自我博弈s1, …, sT。在每个棋局st,执行一个使用最新的神经网络fθ 的MCTS αθ(见图2)。根据MCTS计算的搜索概率来选择落子,at∼πt。根据游戏规则在最终的棋局st记分,来计算比赛的胜出者z。b,AlphaGo Zero中的神经网络训练。神经网络以原始棋盘状态st作为输入,通过参数为θ的多个卷积层,输出代表落子概率分布的向量pt,和一个表示当前玩家在棋局状态st处胜率的标量值vt。神经网络参数θ朝着使策略矢量pt与搜索概率πt相似度最大化的方向更新,同时最大限度地减少预测赢家vt和游戏赢家z之间的误差(见公式(1))。如a所示,在下一次迭代中使用新的参数
MCTS采用神经网络来 fθ 指导它的模拟(见图2)。搜索树中的每个边(s,a)存储先验概率p(s,a)、访问次数n(s,a)和一个动作价值Q(s,a)。每次模拟从根开始,反复选择落子,使置信上限Q(s, a) + U(s, a)最大化,其中U(s, a) ∝ P(s, a) /(1 + N(s, a)) ,直到遇到叶节点s′。叶子的位置被扩展,通过网络对该叶子的棋局进行扩展和评估,产生先验概率和价值(P(s′ , ·),V(s′ )) = fθ(s′ ) 。在模拟中的每条边(s,a)被更新,访问数量N(s,a)增加,并且将其动作值更新为对这些模拟的平均评价
![]()
其中s,a→s’表示在从位置s移动a之后,模拟最终达到s’.

图2 a,每个模拟通过选择具有最大动作值Q,加上取决于存储的先验概率p和该边的访问计数n的一个置信区间上限u(当遍历的时候递增)的边来对树进行遍历。b、叶节点的扩展和对应棋局s的评价是由神经网络(P(S,·)、V(S))= Fθ(S)完成的;p值的向量存储在从s出发的外向边中。c,更新动作价值Q,来跟踪那个落子动作下面的子树中所有评价V的平均值。d,一旦搜索完成后,返回搜索概率π,与N1 /τ成正比,其中N是从根开始的每个落子的访问次数,τ是温度控制参数。
蒙特卡洛可以看作是一个自我博弈算法,给出了神经网络参数θ和根的棋局状态s,计算搜索概率推荐的移动向量π = αθ(s),它与每次落子动作的访问计数的指数成正比,πa ∝ N(s, a)1/τ,其中τ是温度参数.
神经网络通过自我强化学习进行训练,使用MCTS计算每个落子动作。首先,神经网络初始化为随机权重θ0 。在随后的每次迭代i≥1时,产生了自我博弈(图1a)。在每一个时间步t,利用上一次迭代的神经网络执行MCTS搜索 π =αθ − t i 1(st),并且通过概率分布πt 进行采样来落子。当双方放弃行棋时,或者当搜索值低于阈值,或者当比赛超过最大长度时,比赛终止于步骤T;然后为比赛计分,给予奖励 rT∈ {−1,+1}。每个时间步t的数据存储为(st, πt, zt) ,其中zt = ± rT 是在步骤t从当前玩家的视角来看的赢家。并行地(图1b),新的网络参数θi 利用数据(s, π, z)进行训练,数据是从自我博弈的上一次迭代的所有时间步中均匀取样的。调整神经网络(p, v) = fθ (s) ,使预测值v和自我博弈的赢家z之间的误差最小,并且最大限度地提高神经网络移动概率p与搜索概率π的相似度。具体来说,通过使用对均方误差和交叉熵损耗求和的损失函数 l,利用梯度下降来调整参数θ:
![]()
其中,c是一个控制L2权重正则化水平的参数(防止过拟合)
4. AlphaGo Zero 训练的经验分析
应用我们的强化学习流程来训练AlphaGo Zero。训练从完全随机的落子开始,在没有人工干预的情况下持续大约三天。
在训练过程中, 每次MCTS使用1600次模拟,生成了490万场自我博弈,每次落子使用约0.4s的思考时间。使用大小为2048的700000个小批量更新参数。神经网络包含20个残差块。

图 3 a,自我博弈强化学习的表现。图中显示了AlphaGo Zero强化学习在每次迭代i中MCTS αθi 的表现。通过与不同玩家的比赛,来评估ELO评级。在比赛中每次落子的思考时间为0.4秒。为了对比,我们也展示出了使用KGS数据,由人类经验数据进行监督学习训练的模型。b、对人类棋手落子的预测精度。该图显示了在每一次自我博弈迭代i中,神经网络 根据KGS数据集预测人类棋手落子的准确性。通过监督学习的神经网络的训练精度也显示在图中。c,在人类职业比赛结果上的均方误差(MSE)。该图显示了在每一次自我博弈迭代i中,神经网络 从gokifu数据中预测人类职业比赛结果的MSE。MSE是在实际结果z∈ {− 1, +1} 和神经网络的价值v,按1/4的比例缩小到0 - 1的范围之间。图中还显示出经过监督学习训练的神经网络的MSE。
图3a显示了以训练时间为横轴,使用ELO评分规则时AlphaGo Zero在自我博弈强化学习期间的性能。在整个训练期间学习进展顺利,并没有遭受在相关文献中提及的振荡或灾难性的遗忘。令人惊讶的是,在仅训练36小时之后,AlphaGo Zero就超过了AlphaGo Lee的性能,因为AlphaGo Lee训练了几个月。训练72小时后,我们评估AlphaGo Zero,让他和在首尔打败过李世石的AlphaGo Lee使用2小时控制时间和比赛环境下进行比赛。AlphaGo Zero使用具有4个TPU的单机,而AlphaGo Lee则是分布在许多机器上,并且使用48个TPU。AlphaGo Zero以100比0击败AlphaGo Lee。


为了评估自我博弈强化学习相对于使用人类数据进行学习的优势,我们训练了第二个神经网络(使用相同的架构)来预测在KGS服务器数据上人类专业棋手的落子动作,取得了与以前的工作相比更准确的预测精度。
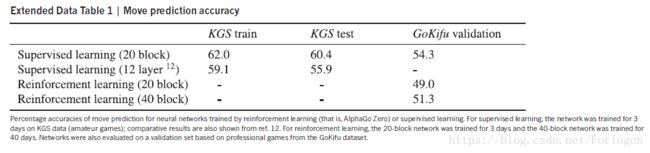
监督学习在一开始获得了非常好的性能,并且更好地预测了人类棋手的动作(图3)。但值得注意的是,虽然监督学习取得了较高的落子预测精度,但是总体而言,这个自学的棋手表现更好,在经过24小时的训练后击败了用人类数据进行训练的程序。这表明,AlphaGo Zero可以学习到完全与人类不同的技能。

图 4 使用单独的(SEP)或联合的策略和价值(dual)网络的神经网络结构比较,以及使用卷积(conv)或残差(res)网络的比较。 ‘dual–res’和‘sep–conv’ 的组合分别与AlphaGo Zero 和 AlphaGo Lee中使用的神经网络结构相对应。每个网络在一个固定的数据集上进行训练,这个数据集是由AlphaGo Zero以前的运行产生的。a,每个训练过的网络与AlphaGo Zero的搜索相结合,来获得不同的程序。通过这些不同的程序之间的比赛来计算ELO评级。在比赛中,每次落子使用5秒的思考时间。b, 每个网络架构对专业人类棋手的落子预测精度(使用gokifu数据集)。c, 每个网络架构在人类专业职业比赛结果的MSE(使用gokifu数据集)
为了将结构和算法的贡献分离,我们将AlphaGo Zero使用的神经网络体系结构的性能与AlphaGo Lee使用的神经网络结构进行了比较(见图4)。我们创建了四个神经网络,就像在AlphaGo Lee中那样,使用独立的策略网络和价值网络;或者使用AlphaGo Lee使用的卷积网络架构或AlphaGo Zero使用的残差网络架构。训练网络时都最大限度地减少相同的损失函数,
![]()
使用的数据集是AlphaGo Zero在72小时的自我博弈训练后产生的固定数据集。利用残差网络更准确,使AlphaGo 达到较低的错误率和性能的改进,达到了超过600Elo。将策略和价值合成一个单一的网络会轻微地降低落子预测精度,但同时降低了价值误差,并且使AlphaGo的性能提高大约600Elo。这是由于提高了计算效率,但更重要的是具有双重目的的网络成为支持多个案例的通用表示。
什麽是ELO?ELO等级分制度是指由匈牙利裔美国物理学家 Arpad Elo创建的一个衡量各类对弈活动水平的评价方法,是当今对弈水平评估的公认的权威方法。ELO怎麽产生的? 最早, ELO等级分制度是基于统计学的一个评估棋手水平的方法. 之后被广泛用于国际象棋、围棋、足球、篮球等运动。线上游戏英雄联盟、魔兽世界内的竞技对战系统也採用此分级制度. 现在不少Destiny网站也使用此统计系统.
5. AlphaGo Zero学习到的知识
AlphaGo Zero在自我博弈训练过程中发现了围棋的新境界。这不仅包括人类围棋知识的基本要素,而且还包括超出传统围棋知识范围之外的非标准策略。
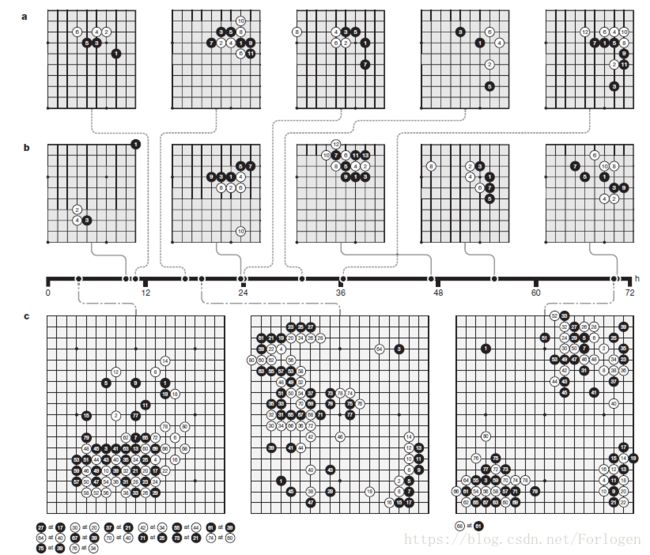
图 5 a,在AlphaGo Zero训练过程中的五个常见的角点序列。在自我博弈训练期间,相关的时间段显示了每个序列第一次形成的时间(考虑旋转和反射)。扩展数据图2提供了每个序列在训练中出现的频率。b,五定式在自我博弈训练的不同阶段被青睐的程度。在自我博弈训练的一次迭代中,在所有的角序列中,每一个显示的角序列都出现的频率最高。该迭代的时间戳在时间轴上表示。在10小时时,弱角移动是首选。在47小时时,3 - 3的入侵是最经常发生的。这个定式在人类职业比赛中也常见。不过AlphaGo Zero随后发现并偏向于这个新变化。扩展数据图3提供了所有五个序列和新变化随时间变化的频率。C,在不同训练阶段进行的三个自我博弈的前80步,每次搜索使用1600次模拟(大约0.4秒)。在3小时后,游戏专注于吃对方的棋子,就像人类初级棋手一样。在19小时时,游戏展现了死活、影响力和占领的基本方面,在70小时时,游戏非常平衡,包括多场战斗和复杂的劫战斗,最终白方以半目赢得胜利。有关完整游戏见补充信息。
图5显示了专业的定式(位于边角的序列上)被发现的时间(图5A和扩展的数据如图2所示);最终AlphaGo Zero使用了新的定式变种(图5B和扩展数据图3)。图5c显示了在不同的训练阶段进行的几次快速自我博弈的进行情况 。在整个训练过程中定期进行的比赛长度在扩展数据图4和补充信息中显示。


(在训练过程中一般游戏长度中都有一些间隔,这些间隔都显示在了额外数据4和补充信息中)AlphaGo Zero迅速从“一块白板”走向成熟,对围棋概念有了深奥理解,包括布局(开放),手筋(战术),活和死,劫(重复的棋盘情况),官子(残局),提子比赛,森特(主动)(初始)、形态(成型)、影响和领土(占领),都能在第一时间迅速掌握。令人惊讶的是,shicho抓住了整个棋盘的序列——在人类学习围棋中比较早被人类掌握的围棋知识点,却在AlphaGo Zero训练比较晚的时候才掌握到。
6. AlphaGo Zero的最后的表现
随后,我们使用更大的神经网络,在一个较长的时间将我们的强化学习流程应用到AlphaGo Zero的第二个实例。训练又从完全随机的行为开始,持续了大约40天。在训练过程中,产生了2900万场自我博弈。参数大小为2048的310万个小批量中更新。神经网络包含40个残差块。学习曲线显示在图6a,在扩展的数据图5中和补充信息中显示了在训练期间定期进行的比赛。
我们通过内部比赛对AlphaGo Fan,AlphaGo Lee和几个以前的Go程序评估了全面训练的AlphaGo Zero。我们还让其对战现有最强的程序,AlphaGo Master——一个基于本文的算法和架构但利用人类数据和特征的算法的程序,于2017年1月在网络游戏上击败了人类最强的职业选手60–0。在我们的评估中,所有程序都只允许使用5秒时间思考每次落子;AlphaGo Zero和AlphaGo Master每个在使用4个TPU的单一机器上进行;AlphaGo Fan和AlphaGo Lee分别分布在176个GPU和48个TPU上。我们还引入一个完全基于AlphaGo Zero原始神经网络的程序,该程序以最大的概率来选择落子。

图 6 a, 使用大型的40块残差网络,训练超过40天的AlphaGo Zero的学习曲线。该学习曲线展示了在我们的强化学习算法中,每次迭代i中的表现。利用不同玩家的比赛计算ELO评级,在游戏中每次搜索使用0.4秒(见方法)。b, AlphaGo Zero的最终性能。AlphaGo Zero 使用40块残差神经网络训练40天。该图显示了AlphaGo Zero、AlphaGo Master(在在线游戏上以60–0击败人体专业顶级选手)、Alpha Lee(击败Lee Sedol)、AlphaGo Fan(击败樊麾),以及以前的围棋程序Crazy Stone,Pachi和gnugo之间的比赛。允许每个程序每次移动使用5秒的思考时间。AlphaGo Zero 和 AlphaGo Master在谷歌云上的单机进行;AlphaGo Fan和AlphaGo Lee分别分布在多台机器上。AlphaGo Zero的原神经网络也包括在内,它没有使用MCTS,直接选择最大概率为的移动。程序以ELO 模式评价:200点的gap相当于75%的胜率。
图6b显示了在Elo量表上每个程序的性能。没有使用任何前向搜索的原始神经网络,Elo评级为3,055。相比之下,AlphaGo Zero达到了5185的等级, AlphaGo Master达到了4858 等级,AlphaGo Lee达到了3739和AlphaGo Fan 达到了3144。
最后,我们使用具有两小时控制时间的100场比赛对AlphaGo Zero和AlphaGo Master进行评估。AlphaGo Zero以89比11赢得了比赛。
7. 讨论
我们的研究结果证明,即便是在最具挑战性的领域中,单纯使用强化学习的方法也是完全可行的:没有人类实例或指导,没有基本规则之外的领域知识,训练达到超人的性能是完全可能的。此外,与通过人类棋手数据进行训练相比,单纯的强化学习方法只需要训练几个小时,并且可以取得更好的渐近性能。使用这种方法,AlphaGo Zero打败了AlphaGo 先前最强的版本,那个版本使用手工制作的特征,利用人类数据进行大幅度训练。
人类从几千年来进行的围棋比赛中积累了大量的知识,并提取其精华写入模式、谚语和书籍。然而在短短几天内,从零开始的AlphaGo Zero能够重新发现很多围棋知识以及新的策略,为这古老的游戏提供了新的见解。
8. 参考文献
1. Friedman, J., Hastie, T. & Tibshirani, R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Springer, 2009).
2. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
3. Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Adv. Neural Inf. Process. Syst. Vol. 25 (eds Pereira, F., Burges, C. J. C., Bottou, L. & Weinberger, K. Q.) 1097–1105 (2012).
4. He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proc. 29th IEEE Conf. Comput. Vis. Pattern Recognit. 770–778 (2016).
5. Hayes-Roth, F., Waterman, D. & Lenat, D. Building Expert Systems (Addison-Wesley, 1984).
6. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).
7. Guo, X., Singh, S. P., Lee, H., Lewis, R. L. & Wang, X. Deep learning for real-time Atari game play using offline Monte-Carlo tree search planning. In Adv. Neural Inf. Process. Syst. Vol. 27 (eds Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N. D. & Weinberger, K. Q.) 3338–3346 (2014). 1 9 o c to b er 2 0 1 7 | VO L 5 5 0 | N AT U R E | 3 5 9
8. Mnih, V. et al. Asynchronous methods for deep reinforcement learning. In Proc. 33rd Int. Conf. Mach. Learn. Vol. 48 (eds Balcan, M. F. & Weinberger, K. Q.) 1928–1937 (2016).
9. Jaderberg, M. et al. Reinforcement learning with unsupervised auxiliary tasks. In 5th Int. Conf. Learn. Representations (2017).
10. Dosovitskiy, A. & Koltun, V. Learning to act by predicting the future. In 5th Int. Conf. Learn. Representations (2017).
11. Man´dziuk, J. in Challenges for Computational Intelligence (Duch, W. & Man´dziuk, J.) 407–442 (Springer, 2007).
12. Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).
13. Coulom, R. Efficient selectivity and backup operators in Monte-Carlo tree search. In 5th Int. Conf. Computers and Games (eds Ciancarini, P. & van den Herik, H. J.) 72–83 (2006).
14. Kocsis, L. & Szepesvári, C. Bandit based Monte-Carlo planning. In 15th Eu. Conf. Mach. Learn. 282–293 (2006).
15. Browne, C. et al. A survey of Monte Carlo tree search methods. IEEE Trans. Comput. Intell. AI Games 4, 1–49 (2012).
16. Fukushima, K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 36, 193–202 (1980).
17. LeCun, Y. & Bengio, Y. in The Handbook of Brain Theory and Neural Networks Ch. 3 (ed. Arbib, M.) 276–278 (MIT Press, 1995).
18. Ioffe, S. & Szegedy, C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proc. 32nd Int. Conf. Mach. Learn. Vol. 37 448–456 (2015).
19. Hahnloser, R. H. R., Sarpeshkar, R., Mahowald, M. A., Douglas, R. J. & Seung, H. S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 405, 947–951 (2000).
20. Howard, R. Dynamic Programming and Markov Processes (MIT Press, 1960).
21. Sutton, R. & Barto, A. Reinforcement Learning: an Introduction (MIT Press, 1998).
22. Bertsekas, D. P. Approximate policy iteration: a survey and some new methods. J. Control Theory Appl. 9, 310–335 (2011).
23. Scherrer, B. Approximate policy iteration schemes: a comparison. In Proc. 31st Int. Conf. Mach. Learn. Vol. 32 1314–1322 (2014).
24. Rosin, C. D. Multi-armed bandits with episode context. Ann. Math. Artif. Intell. 61, 203–230 (2011).
25. Coulom, R. Whole-history rating: a Bayesian rating system for players of time-varying strength. In Int. Conf. Comput. Games (eds van den Herik, H. J., Xu, X. Ma, Z. & Winands, M. H. M.) Vol. 5131 113–124 (Springer, 2008).
26. Laurent, G. J., Matignon, L. & Le Fort-Piat, N. The world of independent learners is not Markovian. Int. J. Knowledge-Based Intelligent Engineering Systems 15, 55–64 (2011).
27. Foerster, J. N. et al. Stabilising experience replay for deep multi-agent reinforcement learning. In Proc. 34th Int. Conf. Mach. Learn. Vol. 70 1146–1155 (2017).
28. Heinrich, J. & Silver, D. Deep reinforcement learning from self-play in imperfect-information games. In NIPS Deep Reinforcement Learning Workshop (2016).
29. Jouppi, N. P. et al. In-datacenter performance analysis of a Tensor Processing Unit. Proc. 44th Annu. Int. Symp. Comp. Architecture Vol. 17 1–12 (2017).
30. Maddison, C. J., Huang, A., Sutskever, I. & Silver, D. Move evaluation in Go using deep convolutional neural networks. In 3rd Int. Conf. Learn. Representations. (2015).
31. Clark, C. & Storkey, A. J. Training deep convolutional neural networks to play Go. In Proc. 32nd Int. Conf. Mach. Learn. Vol. 37 1766–1774 (2015).
32. Tian, Y. & Zhu, Y. Better computer Go player with neural network and long-term prediction. In 4th Int. Conf. Learn. Representations (2016).
33. Cazenave, T. Residual networks for computer Go. IEEE Trans. Comput. Intell. AI Games https://doi.org/10.1109/TCIAIG.2017.2681042 (2017).
34. Huang, A. AlphaGo master online series of games. https://deepmind.com/research/AlphaGo/match-archive/master (2017).



