matlab语言与应用 05 积分变换与复变函数

现代科学运算-matlab语言与应用

东北大学 http://www.icourses.cn/home/ (薛定宇)
《高等应用数学问题的MATLAB求解（第四版）》
代码可在matlab r2016b 运行。

05 积分变换与复变函数问题的计算机求解

05.01 Laplace变换

Laplace变换及其反变换
Laplace变换是科学与工程运算中的重要数学变换
很多学科都源于此变换控制系统的传递函数模型直接由Laplace变换定义

Lplace变换及反变换定义与性质
Laplace变换(拉氏变换)的数学性质
L[f(t)]=∫∞0f(t)e−stdt=F(s) L [ f ( t ) ] = ∫ 0 ∞ f ( t ) e − s t d t = F ( s )
Laplace变换性质
线性性质： L[af(t)±bg(t)]=aL[f(t)]±bL[g(t)] L [ a f ( t ) ± b g ( t ) ] = a L [ f ( t ) ] ± b L [ g ( t ) ] ；其中，a与b均为标量
时域平移性质： L[f(t−a)]=e−asF(s) L [ f ( t − a ) ] = e − a s F ( s )
s-域平移性质： L[e−atf(t)]=F(s+a) L [ e − a t f ( t ) ] = F ( s + a )
微分性质： L[df(t)/dt]=sF(s)−f(0+) L [ d f ( t ) / d t ] = s F ( s ) − f ( 0 + )
n阶微分： L[dndtnf(t)]=snF(s)−sn−1f(0+)−sn−2df(0+)dt−⋯−dn−1f(0+)dtn−1 L [ d n d t n f ( t ) ] = s n F ( s ) − s n − 1 f ( 0 + ) − s n − 2 d f ( 0 + ) d t − ⋯ − d n − 1 f ( 0 + ) d t n − 1
当初值为0时，则 L[dnf(t)dtn]=snF(s) L [ d n f ( t ) d t n ] = s n F ( s )

积分性质：
零初始条件: L[∫t0f(τ)dτ]=F(s)s L [ ∫ 0 t f ( τ ) d τ ] = F ( s ) s
多重积分: L[∫t0⋯∫t0f(τ)dτn]=F(s)sn L [ ∫ 0 t ⋯ ∫ 0 t f ( τ ) d τ n ] = F ( s ) s n
初值性质： limt→0f(t)=lims→∞sF(s) lim t → 0 f ( t ) = lim s → ∞ s F ( s )
终值性质： 如果F(s)没有s≥0的几点，limt→∞f(t)=lims→0sF(s) 如 果 F ( s ) 没 有 s ≥ 0 的 几 点 ， lim t → ∞ f ( t ) = lim s → 0 s F ( s )
卷积性质: L[f(t)∗g(t)]=L[f(t)]L[g(t)] L [ f ( t ) ∗ g ( t ) ] = L [ f ( t ) ] L [ g ( t ) ]
其中卷积算子 * 的定义：
f(t)∗g(t)=∫t0f(τ)g(t−τ)dτ=∫t0f(t−τ)g(τ)dτ f ( t ) ∗ g ( t ) = ∫ 0 t f ( τ ) g ( t − τ ) d τ = ∫ 0 t f ( t − τ ) g ( τ ) d τ
其它性质：
L[tnf(t)]=(−1)ndnF(s)dsn L [ t n f ( t ) ] = ( − 1 ) n d n F ( s ) d s n
L[f(t)tn]=∫∞s⋯∫∞sF(S)dsn L [ f ( t ) t n ] = ∫ s ∞ ⋯ ∫ s ∞ F ( S ) d s n
Laplace反变换：
f(t)=L−1[F(s)]=1j2π∫σ+j∞σ−j∞F(s)estds f ( t ) = L − 1 [ F ( s ) ] = 1 j 2 π ∫ σ − j ∞ σ + j ∞ F ( s ) e s t d s
其中， σ σ 大于函数F(s)奇点的实部

Laplace变换的计算机求解
Laplace变换问题的求解步骤:
L[f(t)]=∫∞0f(t)e−stdt=F(s) L [ f ( t ) ] = ∫ 0 ∞ f ( t ) e − s t d t = F ( s )
符号定义变量t, 再定义时域函数
直接调用laplace()函数
采用默认的t为时域变量
F = laplace(fun)
用户指定时域变量v和复域变量名u
F = laplace(fun, v, u)
调用pretty()或latex()进一步处理结果

Laplace反变换
Laplace反变换计算
函数调用格式：
采用默认的t为时域变量
f = ilaplace(fun)
用户指定时域变量u和复域变量名v
f = ilaplace(fun, u, v)

例5-1 Laplace变换
给定函数 f(t)=t2e−2tsin(t+π) f ( t ) = t 2 e − 2 t sin ⁡ ( t + π )

% Laplace变换
syms t;
f = t^2* exp(-2*t)*sin(t + pi);
F = laplace(f)
% 化简得出的结果
simplify(F),
pretty(ans)

例5-4 函数及导数的变换
给定 f(t)=t2e−2tsin(t+π) f ( t ) = t 2 e − 2 t sin ⁡ ( t + π )
推导 s5L[f(t)] s 5 L [ f ( t ) ] 和 L[d5f(t)/dt5] L [ d 5 f ( t ) / d t 5 ] 之间的关系

syms t s;
f = t^2*exp(-2*t)*sin(t+pi);
F = simplify(laplace(diff(f, t, 5)))
F0 = laplace(f);
simplify(F - s^5 * F0)
% 误差是什么？

初值的影响
考虑到初值条件：

ss = 0;
f1 = f;
for i = 4: -1 : 0
  ss = ss - s^i * subs(f1, t, 0);
  f1 = diff(f1, t);
end;
ss

回忆公式 L[dndtnf(t)]=snF(s)−sn−1f(0+)−sn−2df(0+)dt−⋯−dn−1f(0+)dtn−1 L [ d n d t n f ( t ) ] = s n F ( s ) − s n − 1 f ( 0 + ) − s n − 2 d f ( 0 + ) d t − ⋯ − d n − 1 f ( 0 + ) d t n − 1

例5-5 Laplace变换导数公式推导
前面给出的微分公式不易记忆
试推导出 L[d2f(t)/dt2] L [ d 2 f ( t ) / d t 2 ] 的微分公式

syms t y(t);
laplace(diff(y, t, 2))
% 函数8阶导数的laplace变换
laplace(diff(y, t, 8))

例5-6 导数的Laplace变换
已知 f(t)=e−5tcos(2t+1)+t f ( t ) = e − 5 t cos ⁡ ( 2 t + 1 ) + t
求 L[d5f(t)dt5] L [ d 5 f ( t ) d t 5 ]

syms t;
f = exp(-5*t)*cos(2*t+1) + t;
F = laplace(diff(f, t, 5));
F = simplify(F);
pretty(F)

05.02 数值Laplace变换

Laplace变换问题的数值求解
为什么要研究数值求解？
原函数过于复杂，没有解析解
无需解析表达式，得到图形即可
Laplace反变换数值解析工具
Juraj Valsa 函数: Math Works File Exchange 下载
调用方法: [t, y] = INVLAP(f, t0 t 0 , tf t f , N, other pars)
一般不建议给出other pars，采用默认
注意：函数本身bug，初始时刻不能为0

% INVLAP ?Numerical Inversion of Laplace Transforms 
function [radt,ft]=INVLAP(Fs,tini,tend,nnt,a,ns,nd);
% Fs is formula for F(s) as a string
% tini, tend are limits of the solution interval
% nnt is total number of time instants
% a, ns, nd are parameters of the method 
% if not given, the method uses implicit values a=6, ns=20, nd=19
% it is recommended to preserve a=6
% increasing ns and nd leads to lower error
% an example of function calling  
% [t,ft]=INVLAP('s/(s^2+4*pi^2)',0,10,1001);
% to plot the graph of results write plot(t,ft), grid on, zoom on
FF=strrep(strrep(strrep(Fs,'*','.*'),'/','./'),'^','.^');
if nargin==4
  a=6; ns=20; nd=19;  end;    % implicit parameters
radt=linspace(tini,tend,nnt); % time vector
if tini==0  radt=radt(2:1:nnt);  end;  % t=0 is not allowed
tic                 % measure the CPU time
for n=1:ns+1+nd               % prepare necessary coefficients
   alfa(n)=a+(n-1)*pi*j;
   beta(n)=-exp(a)*(-1)^n;
end;
n=1:nd;
bdif=fliplr(cumsum(gamma(nd+1)./gamma(nd+2-n)./gamma(n)))./2^nd;
beta(ns+2:ns+1+nd)=beta(ns+2:ns+1+nd).*bdif;
beta(1)=beta(1)/2;
for kt=1:nnt                  % cycle for time t
   tt=radt(kt);
   s=alfa/tt;                 % complex frequency s
   bt=beta/tt;
   btF=bt.*eval(FF);          % functional value F(s)
   ft(kt)=sum(real(btF));     % original f(tt)
end;
toc

复杂系统的输出计算
系统框图
U(s)→G(s)→Y(s) U ( s ) → G ( s ) → Y ( s )
用数值方法计算输出
输出信号 Y(s) = G(s)U(s)
系统复杂，如分数阶系统，解析解不能求出
输入为复杂信号，不能求其Laplace变换
输入信号只给出数据点，没有函数

Laplace变换与反变换的数值解

% 扩展代码
function [t,y]=INVLAP_new(G,t0,tn,N,H,tx,ux)
% INVLAP_new - updated version of INVLAP for closed-loop system with any inputs
%
%   [t,y]=INVLAP_new(G,t0,tn,N)
%   [t,y]=INVLAP_new(G,t0,tn,N,H)
%   [t,y]=INVLAP_new(G,t0,tn,N,H,u)
%   [t,y]=INVLAP_new(G,t0,tn,N,H,tx,ux)
%
%   G - the string representation of the open-loop model
%   t0, tn, N - the time interval and number of points in the interval
%   H - the string representation of the feedback model
%   u - the function handle of the input signal
%   tx, ux - the samples of time and input signal
%   y, t - the output and time vectors

% Copyright (c) Dingyu Xue, Northeastern University, China
% Last modified 13 June, 2017 
G=add_dots(G); if nargin<=5, tx='1'; end, if nargin<=4, H=0; end
if ischar(H), H=add_dots(H); end
if ischar(tx), tx=add_dots(tx); end
a=6; ns=20; nd=19; t=linspace(t0,tn,N);
if t0==0, t=t(2:N); N=N-1; end, 
n=1:ns+1+nd; alfa=a+(n-1)*pi*j; bet=-exp(a)*(-1).^n;
n=1:nd; bet(1)=bet(1)/2;
bdif=fliplr(cumsum(gamma(nd+1)./gamma(nd+2-n)./gamma(n)))./2^nd;
bet(ns+2:ns+1+nd)=bet(ns+2:ns+1+nd).*bdif;
if isnumeric(H), H=num2str(H); end
for i=1:N
   tt=t(i); s=alfa/tt; bt=bet/tt; sG=eval(G); sH=eval(H);
   if ischar(tx), sU=eval(tx);
   else
      if isnumeric(tx),
         f=@(x)interp1(tx,ux,x,'spline').*exp(-s.*x);
      else, f=@(x)tx(x).*exp(-s.*x); end
      sU=integral(f,t0,tn,'ArrayValued',true);
   end
   btF=bt.*sG./(1+sG.*sH).*sU; y(i)=sum(real(btF));
end
% remove and add back dots uniformly
function F=add_dots(F)
F=strrep(strrep(strrep(F,'.*','*'),'./','/'),'.^','^');
F=strrep(strrep(strrep(F,'*','.*'),'/','./'),'^','.^');

新函数的调用方法
调用格式
[t, y] = INVLAP_new(G, t0,tn, t 0 , t n , N)
[t, y] = INVLAP_new(G, t0,tn, t 0 , t n , N, H)
[t, y] = INVLAP_new(G, t0,tn, t 0 , t n , N, H, u)
[t, y] = INVLAP_new(G, t0,tn,N,H,tx,ux t 0 , t n , N , H , t x , u x )
负反馈系统

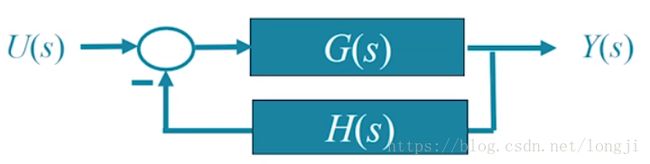
例5-8 分数阶模型的数值Laplace反变换
分数阶模型
G(s)=s0.4+0.4s0.2+0.5s√(s0.2+0.02s0.1+0.6)0.4(s0.3+0.5)0.6 G ( s ) = s 0.4 + 0.4 s 0.2 + 0.5 s ( s 0.2 + 0.02 s 0.1 + 0.6 ) 0.4 ( s 0.3 + 0.5 ) 0.6
Laplace反变换解析解不存在，只能求数值解

G = ['(s^0.4 + 0.4*s^0.2 + 0.5)/' ...
  'sqrt(s)/(s^0.2+0.02*s^0.1+0.6)^0.4/(s^0.3+0.5)^0.6'];
[t, y] = INVLAP_new(G, 0, 1, 10000);
plot(t, y)

例5-9 分数阶模型时域响应
分数阶模型
G(s)=s0.4+0.4s0.2+0.5s√(s0.2+0.02s0.1+0.6)0.4(s0.3+0.5)0.6 G ( s ) = s 0.4 + 0.4 s 0.2 + 0.5 s ( s 0.2 + 0.02 s 0.1 + 0.6 ) 0.4 ( s 0.3 + 0.5 ) 0.6
输入信号: u(t)=e−0.3tsint2 u ( t ) = e − 0.3 t sin ⁡ t 2

f = @(t)exp(-0.3*t).* sin(t.^2);
G = ['(s^0.4 + 0.4*s^0.2 + 0.5)/' ...
  'sqrt(s)/(s^0.2+0.02*s^0.1+0.6)^0.4/(s^0.3+0.5)^0.6'];
tic,
[t, y] = INVLAP_new(G, 0, 15, 400, 0, f);
toc
plot(t, y)
figure();
x0 = 0: 0.2: 15;
u0 = exp(-0.3*x0).* sin(x0.^2);
tic,
[t, y] = INVLAP_new(G, 0, 15, 200, 0, x0, u0);
toc
plot(t, y)

例5-11 闭环系统阶跃响应
开环无理传递函数模型
G(s)=[sinh(0.1s√)0.1s√]21s√sinh(s√) G ( s ) = [ sinh ⁡ ( 0.1 s ) 0.1 s ] 2 1 s sinh ⁡ ( s )
单位负反馈闭环响应计算

G = ['(sinh(0.1*sqrt(s))/0.1/sqrt(s))^2' ...
  '/sqrt(s)/sinh(sqrt(s))'];
[t, y] = INVLAP_new(G, 0, 10, 1000, 1, '1/s');
plot(t, y)

05.03 Fourier变换

Fourier变换及反变换定义与性质
Fourier变换定义: F[f(t)]=∫∞−∞f(t)e−jωtdt F [ f ( t ) ] = ∫ − ∞ ∞ f ( t ) e − j ω t d t
Fourier反变换定义: f(t)=F−1[F(ω)]=12π∫∞−∞F(ω)ejωtdω f ( t ) = F − 1 [ F ( ω ) ] = 1 2 π ∫ − ∞ ∞ F ( ω ) e j ω t d ω

Fourier变换性质
线性性质:其中a与b均为标量
F[af(t)±bg(t)]=aF[f(t)]±bF[g(t)] F [ a f ( t ) ± b g ( t ) ] = a F [ f ( t ) ] ± b F [ g ( t ) ]
平移性质: F[f(t±a)]=e±jaωF(ω) F [ f ( t ± a ) ] = e ± j a ω F ( ω )
复域平移性质： F[e±jatf(t)]=F(ω∓a) F [ e ± j a t f ( t ) ] = F ( ω ∓ a )
微分性质： F[df(t)dt]=jωF(ω) F [ d f ( t ) d t ] = j ω F ( ω )
n阶微分的Fourier变换:
F[dndtnf(t)]=(jω)nF[f(t)] F [ d n d t n f ( t ) ] = ( j ω ) n F [ f ( t ) ]
积分性质： F[∫∞−∞f(τ)dτ]=F(ω)(jω) F [ ∫ − ∞ ∞ f ( τ ) d τ ] = F ( ω ) ( j ω )
n重积分的Fourier变换: F[∫∞−∞⋯∫∞−∞f(τ)dτn]=F[f(t)](jω)n F [ ∫ − ∞ ∞ ⋯ ∫ − ∞ ∞ f ( τ ) d τ n ] = F [ f ( t ) ] ( j ω ) n

Fourier变换的计算机求解
Fourier变换的函数调用格式
默认变量：F = fourier(fun)
v→u v → u : F = fourier(fun, v, u)
Fourier反变换的函数调用格式
默认变量: f = ifourier(fun)
u→v u → v : f = ifourier(fun, u, v)

例5-11 Fourier变换
给定 f(t)=1/(t2+a2),a>0 f ( t ) = 1 / ( t 2 + a 2 ) , a > 0

% Fourier变换
syms t w;
syms a positive,
f = 1/(t^2+a^2);
F = fourier(f, t, w)
% Fourier反变换
f1 = ifourier(F)

例5-12 Fourier变换
给定 f(t)=sin2(at)/t,a>0 f ( t ) = sin 2 ⁡ ( a t ) / t , a > 0

% Fourier变换
syms t w; 
syms a positive;
f = sin(a*t)^2/t;
F = fourier(f, t, w)

得出结果：
F=−πheaviside(−2a−w)li2−πheaviside(2a−w)li2+πheaviside(−w)li F = − π h e a v i s i d e ( − 2 a − w ) l i 2 − π h e a v i s i d e ( 2 a − w ) l i 2 + π h e a v i s i d e ( − w ) l i
手工化简结果：
F[f(t)]={0,|ω|>2a−jπsign(ω)/2,|ω|<2a F [ f ( t ) ] = { 0 , | ω | > 2 a − j π s i g n ( ω ) / 2 , | ω | < 2 a

例5-13 Fourier变换
给定 f(t)=e−a|t|/|t|−−√ f ( t ) = e − a | t | / | t |
Fourier变换的数学手册结果
F=ω2+a2−−−−−−√+a−−−−−−−−−−−√ω2+a2−−−−−−√ F = ω 2 + a 2 + a ω 2 + a 2
使用fourier()命令(早期版本不可用)

syms w t;
syms a positive;
f = exp(-a*abs(t))/sqrt(abs(t));
F = fourier(f, t, w),
pretty(F)

Fourier 正弦和余弦变换
Fourier正弦正反变换的一般定义
F[f(t)]=∫∞0f(t)sinωtdt=Fs(ω) F [ f ( t ) ] = ∫ 0 ∞ f ( t ) sin ⁡ ω t d t = F s ( ω )
F[f(t)]=∫∞0f(t)cosωtdt=Fc(ω) F [ f ( t ) ] = ∫ 0 ∞ f ( t ) cos ⁡ ω t d t = F c ( ω )
F−1s[Fs(t)]=2π∫∞−∞Fs(ω)sin(ωt)dω F s − 1 [ F s ( t ) ] = 2 π ∫ − ∞ ∞ F s ( ω ) sin ⁡ ( ω t ) d ω
F−1c[Fc(t)]=2π∫∞−∞Fc(ω)cos(ωt)dω F c − 1 [ F c ( t ) ] = 2 π ∫ − ∞ ∞ F c ( ω ) cos ⁡ ( ω t ) d ω

例5-13 余弦Fourier变换
给定 f(t)=tne−at,a>0,n=1,2,⋯8 f ( t ) = t n e − a t , a > 0 , n = 1 , 2 , ⋯ 8
试求出其余弦Fourier变换

syms t; syms w real;
syms a positive;
for i = 1:8
  f = t^i*exp(-a*t);
  F = simplify(int(f*cos(w*t), t, 0, inf)),
end

例5.14 分段函数的变换
分段函数 f(t)={cos(t),0<t<a0,others f ( t ) = { cos ⁡ ( t ) , 0 < t < a 0 , o t h e r s
试求其Fourier余弦变换

syms t w;
syms a positive;
f = cos(t);
F = simplify(int(f*cos(w*t), t, 0, a))

离散Fourier正弦、余弦变换
离散Fourier正、余弦变换
Fs(k)=∫a0f(t)sinkπtadt F s ( k ) = ∫ 0 a f ( t ) sin ⁡ k π t a d t
Fc(k)=∫a0f(t)coskπtadt F c ( k ) = ∫ 0 a f ( t ) cos ⁡ k π t a d t
离散Fouriere正、余弦反变换
f(t)=2a∑k=1∞Fs(k)sinkπta f ( t ) = 2 a ∑ k = 1 ∞ F s ( k ) sin ⁡ k π t a
f(t)=1aFc(0)+2a∑k=1∞Fc(k)coskπta f ( t ) = 1 a F c ( 0 ) + 2 a ∑ k = 1 ∞ F c ( k ) cos ⁡ k π t a

例5-15 分段函数
给定 f(t)={t,t≤a/2,a−t,t>a/2 f ( t ) = { t , t ≤ a / 2 , a − t , t > a / 2
其中a > 0,计算其离散Fourier正弦变换

syms t k;
assumeAlso(k, 'integer');
syms a positive;
f1 = t;
f2 = a-t;
Fs = int(f1*sin(k*pi*t/a), t, 0, a/2) + ...
  int(f2*sin(k*pi*t/a), t, a/2, a);
simplify(Fs)
% 由分段函数直接求
f = piecewise('t <= a/2', 't', 't > a/2', 'a-t');
Fs = simplify(int(f*sin(k*pi*t/a), t, 0, a))

快速Fourier变换
离散Fourier变换
X(k)=∑i=1Nxie−2πj(k−1)(i−1)/N, X ( k ) = ∑ i = 1 N x i e − 2 π j ( k − 1 ) ( i − 1 ) / N , where 1≤k≤N 1 ≤ k ≤ N
反变换
x(k)=1N∑i=1NX(i)e2πj(k−1)(i−1)/N, x ( k ) = 1 N ∑ i = 1 N X ( i ) e 2 π j ( k − 1 ) ( i − 1 ) / N , where 1≤k≤N 1 ≤ k ≤ N

快速Fourier变换(Fast Fourier transform,FFT)技术是求离散Fourier变换最实用、也最通用的方法
matlab直接求解: f = fft(x) x^ x ^ = ifft(f)
特点：高效、快速；任意序列长度，长度不要求为 2n 2 n

例5-16 给定信号的FFT
原型函数： x(t)=12sin(2π×t+π/4)+5cos(2π×4t) x ( t ) = 12 sin ⁡ ( 2 π × t + π / 4 ) + 5 cos ⁡ ( 2 π × 4 t )
先FFT，再FFT反变换，看看能否还原

h = 0.01;
t = 0: h:10;
x = 12*sin(2*pi*t + pi/4) + 5*cos(2*pi*4*t);
X = fft(x);
f = t/h/10;
L = floor(length(f)/2);
stem(f(1:L), abs(X(1:L))), xlim([0, 10])
figure();
ix = real(ifft(X));
plot(t, x, t, ix, ':');
xlim([0, 10])

多为FFT
二维FFT
正变换: fft2()
反变换: ifft2()
多维FFT
正变换: fftn()
反变换: ifftn()

05.04 Mellin变换与Hankel变换

Mellin变换
Mellin变换定义： M[f(x)]=∫∞0f(x)xz−1dx=M(z) M [ f ( x ) ] = ∫ 0 ∞ f ( x ) x z − 1 d x = M ( z )
Mellin反变换定义： f(x)=M−1[M(z)]=1j2π∫c+j∞c−j∞M(z)x−zdz f ( x ) = M − 1 [ M ( z ) ] = 1 j 2 π ∫ c − j ∞ c + j ∞ M ( z ) x − z d z

例5-19 Mellin变换
给定 f(t)=lnt/(t+a),a>0 f ( t ) = ln ⁡ t / ( t + a ) , a > 0
试求其Mellin变换

syms t z;
syms a positive;
f = log(t)/(t+a);
M = int(f*t^{z-1}, t, 0, inf)

结果： ⎧⎩⎨⎪⎪⎪⎪⎪⎪x2cos(πz)cos(πz)2−1,a=1∧z≠12∧z∈(0,1)∫∞0tz−1ln(t)a+tdt,a≠1∨z=12∨z∉(0,1) { x 2 cos ⁡ ( π z ) c o s ( π z ) 2 − 1 , a = 1 ∧ z ≠ 1 2 ∧ z ∈ ( 0 , 1 ) ∫ 0 ∞ t z − 1 ln ⁡ ( t ) a + t d t , a ≠ 1 ∨ z = 1 2 ∨ z ∉ ( 0 , 1 )

大部分Mellin变换的解析解不存在

数值Mellin变换
Mellin变换： M[f(x)]=∫∞0f(x)xz−1dx=M(z) M [ f ( x ) ] = ∫ 0 ∞ f ( x ) x z − 1 d x = M ( z )
数值Mellin函数: F = mellin_trans(f, z, pars)

function F = mellin_trans(f, z, varargin)
  f1 = @(x)f(x).*x.^(z-1);
  F = integral(f1, 0, Inf, 'ArrayValued', true, varargin{:});

例5-20 给定函数的Mellin变换
原函数: f(x)=sin(3x0.8)/(x+2)1.5 f ( x ) = sin ⁡ ( 3 x 0.8 ) / ( x + 2 ) 1.5
Mellin变换的解析解不存在，只能求数值解

f = @(x)sin(3*x.^0.8)./(x+2).^1.5;
z = 0:0.05:1;
F = mellin_trans(f, z);
plot(z, F)

Hankel变换及求解
v阶Hankel变换的数学表达式为
H[f(t)]=∫∞0tf(t)Jv(ωt)dt=Hv(ω) H [ f ( t ) ] = ∫ 0 ∞ t f ( t ) J v ( ω t ) d t = H v ( ω )
其中， Jv(⋅) J v ( ⋅ ) 为Bessel函数，J = besselj(v, z)
Hankel反变换公式：
H−1[H(ω)]=∫∞0ωHv(ω)Jv(ωt)dω H − 1 [ H ( ω ) ] = ∫ 0 ∞ ω H v ( ω ) J v ( ω t ) d ω

例5-21 直接积分求Hankel变换
已知函数 f(t)=e−a2t2/2 f ( t ) = e − a 2 t 2 / 2
求 0 阶 Hankel 变换

syms t w a positive;
f = exp(-a^2*t^2/2);
F = int(f*t*besselj(0, w*t), t, 0, inf);
F = simplify(F)
f1 = int(w*F*besselj(0, w*t), w, 0, inf)

数值Hankel变换
Hankel变换公式
H[f(t)]=∫∞0tf(t)Jv(ωt)dt=Hv(ω) H [ f ( t ) ] = ∫ 0 ∞ t f ( t ) J v ( ω t ) d t = H v ( ω )
matlab求解：H = hankel_trans(f, w, mu, pars)

function H = hankel_trans(f, w, mu, varargin)
  F = @(t)t.*f(t).*besselj(mu, w*t);
  H = integral(F, 0, Inf, 'ArrayValued', true, varargin{:});

例5-22 Hankel数值变换
已知函数: f(t)=e−a2t2/2,a=2 f ( t ) = e − a 2 t 2 / 2 , a = 2
选择不同阶次v，用数值方法求出Hankel变换

syms t w a positive;
f = exp(-a^2*t^2/2);
F = int(f*t*besselj(0, w*t), t, 0, inf);
F = simplify(F)
F1 = subs(F, a, 2);
ezplot(F1, [0, 10]);
a = 2;
f = @(t)exp(-a^2*t.^2/2);
w = 0: 0.4: 10;
for i = 0:4
  H = hankel_trans(f, w, i);
  line(w, H);
end
% v = 0与解析解曲线重合

05.05 z变换

z变换及其反变换
z变换并不是积分变换，只是因为其求解方法类似于其它积分变换，故归并到一起
在控制领域，z变换用于离散系统

z变换及反变换定义与性质
离散序列信号 f(k),k=1,2,⋯ f ( k ) , k = 1 , 2 , ⋯
z变换定义： Z[f(k)]=∑k=0∞f(k)z−k=F(z) Z [ f ( k ) ] = ∑ k = 0 ∞ f ( k ) z − k = F ( z )
z变换性质：
线性性质：其中，a与b均为标量
Z[af(k)±bg(k)]=aZ[f(k)]±bZ[g(k)] Z [ a f ( k ) ± b g ( k ) ] = a Z [ f ( k ) ] ± b Z [ g ( k ) ]
时域后向平移性质： Z[f(k−n)]=z−nF(z) Z [ f ( k − n ) ] = z − n F ( z )
前向平移性质: Z[f(k+n)]=znF(z)−∑i=0n−1zn−if(i) Z [ f ( k + n ) ] = z n F ( z ) − ∑ i = 0 n − 1 z n − i f ( i )
零初值： Z[f(k+n)]=znF(z) Z [ f ( k + n ) ] = z n F ( z )
z域比例性质： Z[r−kf(k)]=F(rz) Z [ r − k f ( k ) ] = F ( r z )
频域微分性质： Z[kf(k)]=−zdF(z)dz Z [ k f ( k ) ] = − z d F ( z ) d z
频域积分性质： Z[f(k)k]=∫∞0F(ω)ωdω Z [ f ( k ) k ] = ∫ 0 ∞ F ( ω ) ω d ω
终止性质：
limk→0f(k)=limz→∞F(z) lim k → 0 f ( k ) = lim z → ∞ F ( z )
limk→∞f(k)=limk→1(z−1)F(z) lim k → ∞ f ( k ) = lim k → 1 ( z − 1 ) F ( z )
其中，F(z)无单位圆外的极点
卷积性质: Z[f(k)∗g(k)]=Z[f(k)]Z[g(k)] Z [ f ( k ) ∗ g ( k ) ] = Z [ f ( k ) ] Z [ g ( k ) ]
式中离散信号的卷积算子*定义为
f(k)∗g(k)=∑l=0∞f(k)g(k−l) f ( k ) ∗ g ( k ) = ∑ l = 0 ∞ f ( k ) g ( k − l )
函数F(z) 的 z 反变换定义为
f(k)=Z−1[f(k)]=1j2π∮F(z)zk−1dz f ( k ) = Z − 1 [ f ( k ) ] = 1 j 2 π ∮ F ( z ) z k − 1 d z

z变换求解
z变换求解类似于Laplace变换
函数调用格式：F = ztrans(fun) F = ztrans(fun, k, z)
z反变换的函数调用格式
F = iztrans(fun) F = iztrans(fun, z, k)

例5-23 给定函数求z变换
给定 f(kT)=akT−2+(akT+2)e−akT f ( k T ) = a k T − 2 + ( a k T + 2 ) e − a k T
试求其z变换

syms a T k;
f = a*k*T - 2 + (a*k*T + 2)*exp(-a*k*t);
F = ztrans(f)
pretty(F)

例5-24 总结z反变换公式
给定 F(z)=q(z−1−p)m F ( z ) = q ( z − 1 − p ) m
对不同的m值进行z反变换，总结一般规律

syms p q z;
assume(p ~= 0);
for i = 1:8
  disp(simplify(iztrans(q/(1/z-p)^i))),
end

一般规律：
Z−1[q(z−1−p)m]=(−1)mq(m−1)!pn+m∏i=1m−1(n+i) Z − 1 [ q ( z − 1 − p ) m ] = ( − 1 ) m q ( m − 1 ) ! p n + m ∏ i = 1 m − 1 ( n + i )

双边z变换
k拓展到整个整数空间
Z[f(k)]=∑k=−∞∞f(k)z−k=F(z) Z [ f ( k ) ] = ∑ k = − ∞ ∞ f ( k ) z − k = F ( z )
matlab没有现成函数
可以用底层求和命令直接分段求解
F = symsum(f*z^(-k), k, 0, inf) + symsum(f*z^(-k), k, -inf, -1)

例 5-25 双边z变换
分段函数 f(n)={2n,n≥0−3n,n<0 f ( n ) = { 2 n , n ≥ 0 − 3 n , n < 0

syms z n;
F = symsum(2^n*z^(-n), n, 0, inf) + symsum(-3^n*z^(-n), n, -inf, -1)

结果: F=zz−2+zz−3 F = z z − 2 + z z − 3

有理函数z反变换的数值求解
有理函数的通解 F(z−1) F ( z − 1 )
z−db0+b1z−1+b2z−2+⋯+bm−1z−(m−1)+bmz−ma0+a1z−1+a2z−2+⋯+an−1z−(n−1)+anz−n z − d b 0 + b 1 z − 1 + b 2 z − 2 + ⋯ + b m − 1 z − ( m − 1 ) + b m z − m a 0 + a 1 z − 1 + a 2 z − 2 + ⋯ + a n − 1 z − ( n − 1 ) + a n z − n
z−1 z − 1 的幂级数展开
F(z−1)=f0+f1z−1+f2z−2+⋯=∑k=0∞fkz−k F ( z − 1 ) = f 0 + f 1 z − 1 + f 2 z − 2 + ⋯ = ∑ k = 0 ∞ f k z − k
自定义函数的调用: y = inv_z(num, den, d, N)

function y = inv_z(num, den, varargin)
  [d, N] = default_vals({0,10}, varargin{:});
  num(N) = 0;
  for i = 1:N-d
    k = num(1) / den(1);
    y(d+i) = k;
    if length(num) > 1
      ii = 2:length(den);
      if length(den) > length(num)
        num(length(den)) = 0;
      end
      num(ii) = num(ii)-k*den(ii);
      num(1) = [];
    end;
  end;

function varargout = default_vals(vals, varargin)
  if nargout ~= length(vals)
    error('number of arguments mismatch'); 
  else
    nn = length(varargin) + 1;
    varargout=varargin;
    for i = nn:nargout
      varargout{i} = vals{i};
    end;
  end;
end

例 5-26 数值z反变换
有理数 G(z)=z2+0.4z5−4.1z4+6.71z3−5.481z2+2.2356z−0.3645 G ( z ) = z 2 + 0.4 z 5 − 4.1 z 4 + 6.71 z 3 − 5.481 z 2 + 2.2356 z − 0.3645
变换成
F(z−1)=z−31+0.4z−21−4.1z−1+6.71z−2−5.481z−3+2.2356z−4−0.3645z−5 F ( z − 1 ) = z − 3 1 + 0.4 z − 2 1 − 4.1 z − 1 + 6.71 z − 2 − 5.481 z − 3 + 2.2356 z − 4 − 0.3645 z − 5
求解与绘图

N = 50;
num = [1 0 0.4];
den = [1 -4.1 6.71 -5.481 2.2356 -0.3645];
y = inv_z(num, den, 3, N);
t = 0: (N-1);
stem(t, y)

05.06 复数映射与Riemann曲面

复数矩阵及其变换
函数调用格式(已知复数矩阵z)
共轭复数矩阵: Z1 Z 1 = conj(Z)
实部、虚部提取: R = real(Z) I = imag(Z)
幅值、相位表示: A = abs(Z) P = angle(Z)

复变函数映射

例5-28 已知复变函数 f(z)=z2+3z+1(z−1)5 f ( z ) = z 2 + 3 z + 1 ( z − 1 ) 5
求 f(3)(−j5–√) f ( 3 ) ( − j 5 )

syms z;
f = (z^2 + 3*z + 4)/(z-1)^5;
f3 = diff(f, z, 3);
d3 = subs(f3, z, -sqrt(-5))

复函数的映射(变量替换)
平移: z=ω+γ z = ω + γ
反演: z=1/ω z = 1 / ω
双线性: z=(aω+b)/(cω+d) z = ( a ω + b ) / ( c ω + d )

例5-29 双线性变换映射
已知函数 f(z)=z2+3z+4(z−1)5 f ( z ) = z 2 + 3 z + 4 ( z − 1 ) 5
双线性变换： z=s−1s+1 z = s − 1 s + 1
直接映射:

syms z s;
f = (z^2 + 3*z + 4)/(z-1)^5;
F = simplify(subs(f, z, (s-1)/(s+1)))

例5-30 单位圆内样本点映射
左半平面点映射

[x, y] = meshgrid(-1: 0.1: 1);
ii = find(x.^2+y.^2 <= 1);
x = x(ii);
y = y(ii);
z = x + sqrt(-1)*y;
plot(z, '+');
hold on;
ezplot('x^2+y^2=1')
figure;
s = (z-1)./(z+1);
plot(s, 'x')

Riemann曲面绘制
复变函数映射图形绘制步骤
生成网格 z = cplxgrid(n)
计算数据：通过点运算计算函数值，如
f = z.^3.*sin(z.^2)
绘图(Riemann曲面): cplxmap(z, f)

function cplxmap1(z,w,B)
%CPLXMAP Plot a function of a complex variable.
%   CPLXMAP(z,f(z),(optional bound))
%   Used by CPLXDEMO.
%
%   See also CPLXGRID.

%   Copyright 1984-2002 The MathWorks, Inc. 
%   $Revision: 5.8 $  $Date: 2002/04/15 03:30:08 $
%   modified by Dingyu Xue for multi-valued complex functions
blue = 0.2;
x = real(z);
y = imag(z);
u = real(w);
v = imag(w);

if nargin > 2
   k = find((abs(w) > B) | isnan(abs(w)));
   if length(k) > 0
      u(k) = B*sign(u(k));
      v(k) = zeros(size(k));
      v = v/max(max(abs(v)));
      v(k) = NaN*ones(size(k));
   end
end

M = max(max(u));
m = min(min(u));
axis([-1 1 -1 1 m M]);
caxis([-1 1]);
s = ones(size(z));
surf(x,y,u,v);
colormap(hsv(64))

例5-31 Riemann曲面
复变函数 f(z)=z3sinz2 f ( z ) = z 3 sin ⁡ z 2

% 绘制Riemann曲面
z = cplxgrid(50);
f = z.^3.*sin(z.^2);
cplxmap(z, f)

多值 f(z)=z√n f ( z ) = z n 函数的Riemann曲面
方根函数的绘制 cplxroot(n)

例5-32 绘制Riemann面 z√3,z√4 z 3 , z 4

cplxroot(3), figure, cplxroot(4)

该函数只能绘制方根函数，对其它多值复变函数无能为力

例5-32 重绘三次方跟曲面
三次方根函数的三个分支 z√3 z 3
一个分支： f1(z)=z√3 f 1 ( z ) = z 3
其余两个分支: f1(z)e−2jπ/3,f1(z)e−4jπ/3 f 1 ( z ) e − 2 j π / 3 , f 1 ( z ) e − 4 j π / 3
直接绘制：

z = cplxgrid(30);
f1 = z.^(1/3);
a = exp(-2i*pi/3);
cplxmap1(z, f1), hold on;
cplxmap1(z, a*f1);
cplxmap1(z, a^2*f1);
zlim([-1, 1]), hold off;

优点：果能求出所有的分支，可以扩展到其它多值函数

05.07 奇点、极点与留数

留数的概念与计算
若函数f(z)在复平面的区域内各点处均为单值，且其导数为有限值，则称f(z)在复平面内为解析的
单支函数不解析的点称为奇点
使得f(z)分母多项式等于零的奇点又称为极点
如果 z = a 为f(z)函数的单奇点，则留数的定义为
Res[f(z),z=a]=limz→a(z−a)f(z) R e s [ f ( z ) , z = a ] = lim z → a ( z − a ) f ( z )
单极点留数: c = limit(F*(z-a), z, a)

重奇点的留数
若 z = a 为函数 f(z) 的 m 重奇点，则该点的留数定义为
Res[f(z),z]=limz→a1(m−1)!dm−1dzm−1[f(z)(z−a)m] R e s [ f ( z ) , z ] = lim z → a 1 ( m − 1 ) ! d m − 1 d z m − 1 [ f ( z ) ( z − a ) m ]
m重奇点的计算: c = limit(diff(F*(z-a)^m, z, m-1)/prod(1:m-1), z, a)

奇点与重数的计算
matlab调用格式: [p, m] = poles(f)
直接计算极点与留数 [r, p, m] = residuesym(f, a, b)

function [r, p, m] = residuesym(f, a, b)
  z = symvar(f);
  if nargin == 1
    [p, m] = poles(f);
  else
    [p, m] = poles(f, a, b);
  end;
  for k = 1: length(p)
    r(k) = limit(diff(f*(z-p(k))^m(k), z, m(k)-1) ...
       /factorial(m(k)-1), z, p(k));
  end;

例5-34 求奇点与留数
计算下式留数
f(z)=1z3(z−1)sin(z+π3)e−2z f ( z ) = 1 z 3 ( z − 1 ) s i n ( z + π 3 ) e − 2 z
找出奇点z = 0, z = 1

syms z;
f = sin(z + pi/3)*exp(-2*z)/(z^3*(z-1))
F1 = limit(diff(f*z^3, z, 2)/prod(1:2), z, 0),
F2 = limit(f*(z-1), z, 1)
[r, p, m] = residuesym(f)

例5-35 奇点的重数
函数 f(z)=sin