Diversity-Driven Exploration Strategy for Deep Reinforcement Learning
Diversity-Driven Exploration Strategy for Deep Reinforcement Learning
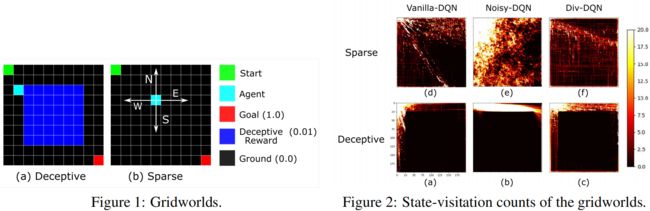
文章来自清华大学,主要解决的问题是 RL 的探索问题,文中的方法对拥有large state space, sparse reward, deceptive reward的任务很有效。
一般的RL探索方法:
- ϵ \epsilon ϵ greedy or entropy regularization;
- provide bonus rewards after visiting a novel state;
- add random noise to the action/parameter space;
本文的具体做法是:
在 off- or on- policy DRL的损失函数中加入一项策略距离的度量,则新的损失函数表达式为:
L L L是原本DRL算法的损失函数, α \alpha α是超参数。公式的直觉理解是,当current policy 与past policy的距离越小,则损失函数 L D L_D LD变得越大,这就给DRL的优化算法提供了一个信息,即告诉算法需要去找一个current policy使得其与之前的pass policy 距离更远。
Contribution:
1)修改了DRL的损失函数,进而增加了算法的探索性。
2)给出了损失函数中超参数 α \alpha α的计算方法。
文中用了三个算法进行实验,A2C(on-policy), DQN(off-policy, discrete), DDPG(off-policy, continuous),在此先列出原DRL算法的loss functions:
L A 2 C _ a c t o r = − E s , a ∼ π [ G t − V ( s ) + β H ( π ( . ∣ s , θ ) ) ] L_{A2C\_actor}=-\mathbb{E}_{s,a\sim \pi}[G_t - V(s) + \beta H(\pi(.|s,\theta))] LA2C_actor=−Es,a∼π[Gt−V(s)+βH(π(.∣s,θ))]
L D Q N = E s , a , r , s ′ ∼ U ( z ) [ ( r ( s , a ) + γ m a x a ′ Q ( s ′ , a ′ , θ − ) − Q ( s , a , θ ) ) 2 ] L_{DQN}=\mathbb{E}_{s,a,r,s'\sim U(z)}[(r(s,a)+\gamma max_{a'}Q(s',a',\theta^-) -Q(s,a,\theta))^2] LDQN=Es,a,r,s′∼U(z)[(r(s,a)+γmaxa′Q(s′,a′,θ−)−Q(s,a,θ))2]
L D D P G _ a c t o r = − E s ∼ z [ Q ( s , π ( s ) ) ] L_{DDPG\_actor}=-\mathbb{E}_{s\sim z}[Q(s,\pi(s))] LDDPG_actor=−Es∼z[Q(s,π(s))]
(备注:A2C使用熵 H ( π ( . ∣ s , θ ) ) H(\pi(.|s,\theta)) H(π(.∣s,θ))进行探索, DQN用 ϵ − \epsilon- ϵ−greedy探索,而DDPG用随机策略 π ^ ( s ) = π ( s ) + N \hat\pi(s)=\pi(s)+N π^(s)=π(s)+N探索,其中 N N N为OU过程噪声)
然后修改上面的loss functions:
由于添加项引入了超参数 a scaling factor α \alpha α,然后文章给出了确定该超参数的办法。其中,Off-policy方法只要用distance-based,而On-policy方法要结合distance-based 和 performance-based两者一起用。