强化学习(RLAI)读书笔记第十三章策略梯度方法(Policy Gradient Methods)
强化学习(RLAI)读书笔记第十三章策略梯度方法(Policy Gradient Methods)
- 13.1 Policy Approximation and its Advantages
- 13.2 The Policy Gradient Theorem
- 13.3 REINFORCE: Monte Carlo Policy Gradient
- 13.4 REINFORCE with Baseline
- 13.5 Actor-Critic Methods
- 13.6 Policy Gradient for Continuing Problems
- 13.7 Policy Parameterization for Continuous Actions
- 13.8 Summary
目前为止本书讲述的方法基本都是动作值函数的方法。这一章介绍一个学习参数化策略的方法,这个方法中不需要考虑值函数就可以得到策略。在学习策略参数的时候有可能还会用到值函数,但是选择动作的时候不需要。使用了一个 θ ∈ R d ′ \theta\in\mathbb R^{d'} θ∈Rd′作为策略的参数向量,然后用 π ( a ∣ s , θ ) = P r { A t = a ∣ S t = s , θ t = θ } \pi(a|s,\theta)=Pr\{A_{t}=a|S_{t}=s,\theta_{t}=\theta\} π(a∣s,θ)=Pr{At=a∣St=s,θt=θ}来表示时间t时选择动作a时的概率。这一章考虑一个使用 J ( θ ) J(\theta) J(θ)表示的度量函数的梯度来学习策略参数的算法。
这个方法是来最大化 J ( θ ) J(\theta) J(θ)的,因此参数的更新近似对于J的梯度上升:
θ t + 1 = θ t + α ∇ J ( θ t ) ^ \theta_{t+1} = \theta_{t}+\alpha\widehat{\nabla J(\theta_{t})} θt+1=θt+α∇J(θt) ,
对于所有满足此类更新形式的算法,不论是否计算值函数都叫做policy gradient methods。那些同时计算策略函数和值函数的方法又叫做actor-critic算法,actor表示学好的策略,而critic表示学好的值函数。
13.1 Policy Approximation and its Advantages
对于策略梯度算法,策略可以被任意的参数化,只要最后的函数 π ( a ∣ s , θ ) \pi(a|s,\theta) π(a∣s,θ)是一个对于其参数可微的函数。这实际上要求学出来的算法不能使确定性的。
对于那些离散且不大的动作空间,一个简单常用的参数化方法是对于每一个状态动作对都构造一个参数化数值 h ( s , a , θ ) ∈ R h(s,a,\theta)\in R h(s,a,θ)∈R作为其优先级的表示。对于比较高优先值的动作选择的概率就比较大,比如可以根据如下指数softmax的分布:
π ( a ∣ s , θ ) ≐ e h ( s , a , θ ) ∑ b e h ( s , b , θ ) \pi(a|s,\theta)\doteq \dfrac{e^{h(s,a,\theta)}}{\sum_{b}e^{h(s,b,\theta)}} π(a∣s,θ)≐∑beh(s,b,θ)eh(s,a,θ)
这个形式的策略参数化我们叫做动作优先值的soft-max。动作优先值可以被任意地参数化。比如可以直接使用一个神经网络来逼近,或者只使用简单的线性特征的形式:
h ( s , a , θ ) = θ T x ( s , a ) h(s,a,\theta)=\theta^{T}x(s,a) h(s,a,θ)=θTx(s,a)
参数化策略的方法一大优势是可以逼近确定性策略,而对于建立在值函数之上的 ϵ \epsilon ϵ-greedy算法来说不可能做到,因为总要对非最优动作分配 ϵ \epsilon ϵ部分的概率。
参数化策略第二个优势是可以支持对于动作任意分配概率。某些问题里可能采取任意的动作才是最优的。基于动作值函数的策略就不能自然地支持这一功能。
第三个优势是某些问题里策略可能是一个更简单的函数近似的对象。最后一个优势是策略的参数化有时是强化学习算法里注入关于目标策略的先验知识的方法。
13.2 The Policy Gradient Theorem
参数化策略相对于 ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法除了实用的优势之外,还有这一个重要的理论优势。对于连续的参数化策略,动作概率作为一个已学习参数的函数是连续变化的,不像是 ϵ − g r e e d y \epsilon-greedy ϵ−greedy有可能是突变。可能主要因为这个特点所以policy-gradient方法有着更强的收敛特性。特别是策略对于参数的连续性使得这个方法能够逼近梯度上升算法。
这一节我们考虑episodic形式的任务,我们定义策略的性能为从起始状态开始的反馈,即:
J ( θ ) ≐ v π θ ( s 0 ) J(\theta)\doteq v_{\pi_{\theta}}(s_{0}) J(θ)≐vπθ(s0)
这里把discounting参数 γ \gamma γ设为1。
使用了函数逼近之后,把策略参数往保证策略更好的方向改变看起来有些困难。问题在于策略的性能依赖于动作的选择以及在选择动作时依赖的状态分布。这两个部分都被策略参数影响。对于一个状态,策略参数对于动作和奖励的影响可以通过参数直接计算出来。但是策略对于状态分布的影响是有关环境的函数而且一般不知道。我们没有办法计算出一个有关于策略改变对于状态分布的影响的梯度。因为这个影响是未知的。
但是幸运的是,对于这个问题有一个完美的理论答案,叫做policy gradient theorem,书上有推导。它为性能函数J相对于策略参数的梯度提供了解析表达。表明了这个梯度与状态分布的求导无关。episodic形式的policy gradient theorem推导出:
∇ J ( θ ) ∝ ∑ s μ ( s ) ∑ a q π ( s , a ) ∇ π ( a ∣ s , θ ) \nabla J(\theta) \propto \sum_{s}\mu(s)\sum_{a}q_{\pi}(s,a)\nabla\pi(a|s,\theta) ∇J(θ)∝∑sμ(s)∑aqπ(s,a)∇π(a∣s,θ)。
13.3 REINFORCE: Monte Carlo Policy Gradient
现在考虑推导出第一个policy-gradient的学习算法。policy gradient theorem的右端是一个根据目标策略 π \pi π下状态分布进行的加权求和。只要遵循策略 π \pi π那么这些状态就会根据这个分布的比例被访问。于是推导得:
∇ J ( θ ) ∝ ∑ s μ ( s ) ∑ a q π ( s , a ) ∇ π ( a ∣ s , θ ) = E π [ ∑ a q π ( S t ∣ , a ) ∇ π ( a ∣ S t , θ ) ] \nabla J(\theta) \propto \sum_{s}\mu(s)\sum_{a}q_{\pi}(s,a)\nabla\pi(a|s,\theta) \\ \qquad\quad = E_{\pi} [\sum_{a}q_{\pi}(S_{t}|,a)\nabla \pi(a|S_{t},\theta) ] ∇J(θ)∝∑sμ(s)∑aqπ(s,a)∇π(a∣s,θ)=Eπ[∑aqπ(St∣,a)∇π(a∣St,θ)]
在这里我们可以把随机梯度上升法写作
θ t + 1 ≐ θ t + α ∑ a q ^ ( S t , a , w ) ∇ π ( a ∣ S t , θ ) \theta_{t+1}\doteq \theta_{t}+\alpha\sum_{a}\widehat{q}(S_{t},a,w)\nabla \pi(a|S_{t},\theta) θt+1≐θt+α∑aq (St,a,w)∇π(a∣St,θ)
这个算法叫做all-actions方法,因为它的更新包含了所有动作,是很有前景并且值得研究的,不过目前我们的算法只关注当前动作 A t A_{t} At。
通过进一步的推导,我们可以继续将上式推导为以下形式:

最后一个等式括号里的正式我们所要的。因此使用这个式子的一个采样来作为我们泛型算法的一个实例的REINFORCE update:

这个更新是有其内部逻辑的。每次增量都正比于反馈估计值 G t G_{t} Gt,也就是对于反馈值比较大的就沿着其梯度方向增大较多。反比与采取动作的概率,这样能够防止那些经常被访问的状态占据大多数更新。
这里的REINFORCE使用的是从时间t开始的完全反馈,因此是一种MC算法。这个算法对于episodic形式来说需要等待episode结束才能够计算整体的反馈。整体算法伪代码如下:

伪代码里和推导的部分有些不一样,其中梯度的推导写为对ln的梯度。这个对ln求梯度的向量也叫作eligibility vector。第二个不一样的地方是伪代码里有discounting系数 γ \gamma γ,之前的推导里这个系数都为1.在这里需要一些对于推导的调整才能得到伪代码里的公式。
作为一个随机梯度方法,REINFORCE法有一个良好的理论收敛性质。通过构造可以使得期望更新的方向和评估函数梯度方向一直,这就保证了对于足够小的参数 α \alpha α算法一定能够收敛到一个局部最优。但是MC形式的REINFORCE方法会带来较大的方差和较慢的学习速度。
13.4 REINFORCE with Baseline
policy gradient theorem可以被泛化为一个动作值函数与任意baseline的比较值:
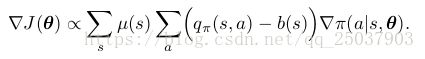
这个baseline可以是任意的函数,甚至是个随机变量。只要是它和动作无关即可。因为增加的项和为0:

带baseline的policy gradient theorem可以被用来推导出一个新的形式的更新公式:
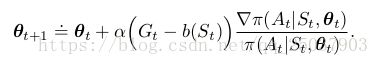
总的来说这个增加的baseline对于更新的期望值没有影响,但是会极大的减小它的方差。很自然的选择每个状态值函数的估计值 v ^ ( S t , w ) \widehat{v}(S_{t},w) v (St,w)作为算法的baseline。其中的w是之前章节里介绍的值函数近似的参数。
算法的伪代码如下:

其中对于值函数估计中的系数 α w \alpha^{w} αw有一个简单的设定策略,但是对于策略系数 α θ \alpha^{\theta} αθ并没有什么清楚的设定方式。
13.5 Actor-Critic Methods
尽管带baseline的REINFORCE算法同时使用了策略函数和状态值函数,但是我们不认为它是一个actor-critic算法因为它的值函数只作为一个baseline而没有作为一个critic。也就是说它没有用来作为自举,而是只作为一个更新的baseline。这是一个很简单的区分方式,因为只有使用了自举的方式才能够带来偏差和一个对于函数近似量的渐进依赖。自举带来的偏差和对于状态表示的依赖是有益的,一般会减少方差并且加速收敛。带baseline的REINFORCE算法是无偏的并且会渐进收敛到局部最小值,但是MC形式的算法一般会学习的很慢而且不方便应用到online问题和continuing问题。前面讲过使用TD形式的方法能够克服这些不方便,并且通过多步反馈方法能够调节自举的程度。为了能够利用这些优势,我们使用一个带自举的critic的actor-critic方法。
首先考虑一步TD算法。一步算法的优点在于它们是完全在线并且增量式的,而且减少了使用资格迹的复杂度。它们是资格迹方法的特殊形式,尽管不通用但是容易理解。一步actor-critic方法更新如下:
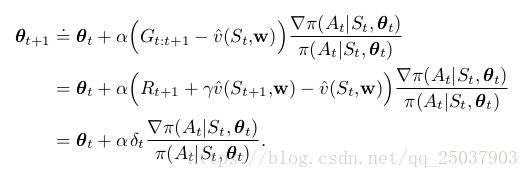
一个自然的和这个算法相伴的状态值函数的学习方法是半梯度TD(0)算法,用来更新对于值函数的估计。伪代码如下:

将这个算法延伸到forward view的n步算法以及 λ \lambda λ-return形式的算法是很直接的。对于拓展到使用资格迹的backward view形式的 λ − r e t u r n \lambda-return λ−return形式的actor-critic算法也很简单,方法如下:

13.6 Policy Gradient for Continuing Problems
就像10.3讨论的一样,对于没有episode界限的continuing形式的问题我们需要定义一个新形式的性能评估函数,利用之前介绍的每一时间步的平均奖励:

其中 μ \mu μ表示的是在策略 π \pi π下的稳定状态分布,建立在ergodicity假设的基础上。对于continuing形式的backward view形式的actor-critic算法如下:

对于连续形式下的policy gradient theorem的推导有不同的证明,书上有。
13.7 Policy Parameterization for Continuous Actions
基于策略的方法提供了以一个简单的方式来解决大规模动作空间的问题,甚至可以解决一个有无限个动作的连续空间也可以。我们不再学习每个动作的概率,而是学习采取动作的概率分布。
为了构造一个参数化的策略,策略可以被定义为一个分布在实数标量值的动作上的高斯分布。其中的均值和标准差是依赖于动作和给定参数的近似函数。也就是:
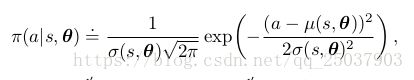
其中的均值和方差被参数化为:
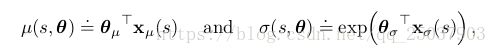
因此{对于整个策略而言参数即为两个部分参数的组合 θ = [ θ μ , θ σ ] T \theta=[\theta_{\mu},\theta_{\sigma}]^{T} θ=[θμ,θσ]T。
13.8 Summary
这一章之间介绍的都是动作值函数的方法。这一章我们介绍了直接学习参数化策略的方法,这个方法能够直接决定策略而不需要去查询动作值函数估计。特别的考虑到policy gradient menthod,也就是每一步都朝着性能评估函数的梯度方向更新策略参数的方法。
学习和存储策略参数的方法有很多优点:第一可以直接学习采取动作的概率。第二可以同时进行一定程度的exploration和渐进得到确定性策略。第三它可以自然地解决连续动作空间的问题。这些对于策略参数方法都很自然但是对于值函数方法很难解决。特别是,有些问题里对于策略的直接建模学习可能会更简单。
REINFORCE方法直接遵从了policy gradient theorem。增加一个值函数估计来减少算法的方差而且不会增加偏差。使用值函数来进行自举会引入偏差,但是通常会减小方差和加速学习。状态值函数向选择动作来分配评价,也就是作为critic,而选择动作的策略叫做actor,一起组成了actor-critic算法。
policy-gradient算法提供了一组同动作值函数方法优缺点都很不同的算法。现在我们对它的了解还不多,但是是个很让人兴奋很值得研究的领域。