policy gradient 的理解
参考:策略梯度理解及TensorFlow实现
李宏毅深度强化学习笔记(二)Proximal Policy Optimization (PPO)
李宏毅,深度强化学习
DQN的缺点:
在DQN中,我们通过神经网络计算价值函数Q(s,a,w)近似表示Q(s,a),即:
Q ( s , a , w ) ≈ Q ( s , a ) Q(s,a,w) \approx Q(s,a) Q(s,a,w)≈Q(s,a)
这个函数用参数w来描述。我们是根据最大的价值选择动作。
在策略梯度法中,采取类似的思路,这是是对策略近似表示,即:
π θ ( s , a ) = P ( a ∣ s , θ ) ≈ π ( s , a ) {\pi _\theta }(s,a) = P(a|s,\theta ) \approx \pi (s,a) πθ(s,a)=P(a∣s,θ)≈π(s,a)
这个策略函数用参数 θ \theta θ描述。因为是概率,所以是个连续函数,可以直接跳过用值函数进行评估,直接用梯度上升(或者下降)求最优的策略。
对于dqn,对连续动作的处理不足,我们都知道DQN的Q网络输入为离散的state,输出为action,无法处理连续的动作。
策略梯度法(PD)
为什么采取pd
- 基于策略的学习可能会具有更好的收敛性,这是因为基于策略的学习虽然每次只改善一点点,但总是朝着好的方向在改善;但是上讲提到有些价值函数在后期会一直围绕最优价值函数持续小的震荡而不收敛。
- 在那些拥有高维度或者连续状态或者动作空间的问题中,使用基于价值的方法在得到价值后,往往需要比较每个行为的价值大小,因为维度高,则找出最大值往往需要花费很多时间。( 对于dqn,对连续动作的处理不足,我们都知道DQN的Q网络输入为离散的state,输出为action,无法处理连续的动作。)
- 回顾DQN中,是根据众多行为中价值最大得一个进行选择,是一种确定性的策略。而有些问题中的最优策略往往是随机的。
理论推导:
agent可能在每次玩游戏的时候走的路径都不一定完全相同。假设策略会引导agent经历一个轨迹。
τ = ( s 1 , a 1 , s 2 , a 2 , ⋯ s T , a T ) \tau = \left( {{s_1},{a_1},{s_2},{a_2}, \cdots {s_T},{a_T}} \right) τ=(s1,a1,s2,a2,⋯sT,aT)
如下图:
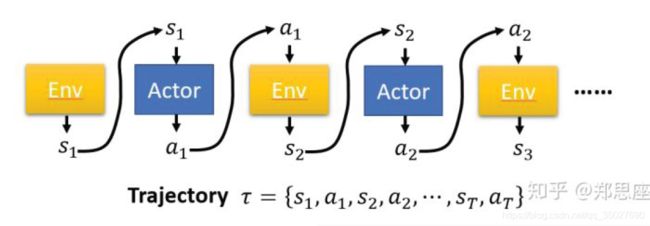
定义:这条轨迹在策略 π \pi π的引导下出现的概率:
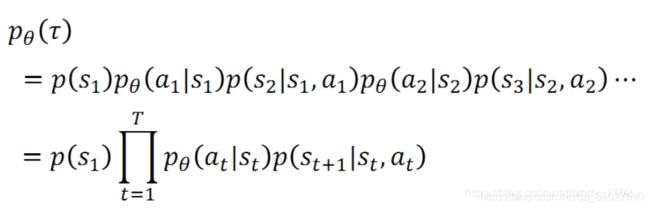
R ( τ ) = ∑ t = 1 T r t R\left( \tau \right) = \sum\limits_{t = 1}^T {{r_t}} R(τ)=t=1∑Trt是某一条轨迹的的总汇报,是一个随机变量。因为轨迹是个随机变量
因为轨迹是个随机变量,所以最好的方法是对该回报求期望,有:
J ( θ ) = E τ ∼ P θ ( τ ) R ( τ ) = ∑ τ R ( τ ) P θ ( τ ) J\left( \theta \right) = {E_{\tau \sim {P_\theta }\left( \tau \right)}}R\left( \tau \right) = \sum\limits_\tau {R\left( \tau \right)} {P_\theta }\left( \tau \right) J(θ)=Eτ∼Pθ(τ)R(τ)=τ∑R(τ)Pθ(τ)
我们希望期望最大化,所以需要对其求梯度,注意这里是对参数θ求偏导:

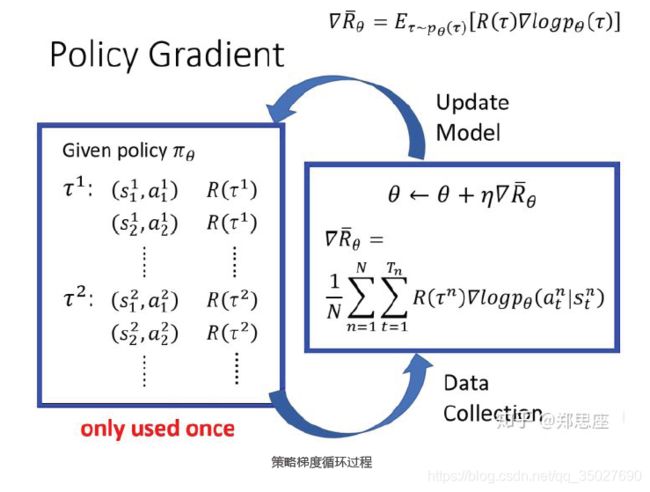
图中即为梯度公式,然后根据梯度上升公式更新参数θ, θ ← θ + η ∇ θ J ( θ ) \theta \leftarrow \theta + \eta {\nabla _\theta }J\left( \theta \right) θ←θ+η∇θJ(θ)。注意这里有几个转换的过程.
- 对概率加权的reward求和就是求reward的期望,因此有红框部分的改写;
- 因为训练的过程中会进行采样训练,采样个数为N,因此公式可以近似表示为N次采样得到的reward的平均。
- 因为: log P θ ( τ ) = log P ( s 1 ) + ∑ t = 1 T log π θ ( a t ∣ s t ) + ∑ t = 1 T log p ( s t + 1 ∣ s t , a t ) \log {P_\theta }\left( \tau \right) = \log P\left( {{s_1}} \right) + \sum\limits_{t = 1}^T {\log } {\pi _\theta }({a_t}|{s_t}) + \sum\limits_{t = 1}^T {\log } p({s_{t + 1}}|{s_t},{a_t}) logPθ(τ)=logP(s1)+t=1∑Tlogπθ(at∣st)+t=1∑Tlogp(st+1∣st,at),所以有: ∇ log P θ ( τ ) = ∑ t = 1 T ∇ θ log π θ ( a t ∣ s t ) \nabla \log {P_\theta }\left( \tau \right) = \sum\limits_{t = 1}^T {{\nabla _\theta }\log } {\pi _\theta }({a_t}|{s_t}) ∇logPθ(τ)=t=1∑T∇θlogπθ(at∣st),因为只是对参数θ求导。(这里 π θ {\pi _\theta } πθ同pθ,都是指转移概率)
- 最后一项中,可以将第n条轨迹的累积回报 R ( τ n ) R\left( {{\tau ^n}} \right) R(τn)看成对后面对数概率的加权,相当于单个时间内总奖励越高的 τ \tau τ越用力拉拢概率密度函数,使得概率密度方向向总奖励更高的轨迹方向移动,最大化高奖励轨迹 τ \tau τ出现的概率。
更新梯度的流程如下:
存在的问题
上面提到第n条轨迹的累积回报 R ( τ n ) R\left( {{\tau ^n}} \right) R(τn)可看成对后面对数概率的加权。但是会出现两个问题:
- 梯度策略的初衷是提高好动作的概率而降低差动作的概率,而上面公式中 R ( τ n ) R\left( {{\tau ^n}} \right) R(τn)可能全为正,会导致所有的策略增强。
- R ( τ ) = ∑ t = 1 T r t R\left( \tau \right) = \sum\limits_{t = 1}^T {{r_t}} R(τ)=t=1∑Trt是某一条轨迹的的总汇报,对于轨迹中的每一个时间点元组 ( s t , a t ) ({s_t},{a_t}) (st,at),都是用总时间的回报和来进行加权的,理论上分析这样是不合理的。
t时刻所做的动作只能影响t时刻之后的回报,而不应该影响t时刻之前的。这两个问题会导致结果出现较大波动,即较大的方差,这是策略梯度算法最大的缺陷。
改进方法
针对问题1,Williams等人提出了REINFORCE算法。即添加基线,即把权重项变为 R ( τ n ) − b R\left( {{\tau ^n}} \right)-b R(τn)−b,这里b指基线。通常b取 E ( R ( τ n ) ) E\left( {R\left( {{\tau ^n}} \right)} \right) E(R(τn)),也就是对所有的权重求期望,然后分别用每个权重减掉这个值,最后可给差的策略以负的权重。可用来减少方差。
针对问题2,引入合理的评价方法,即把权重项变为 ∑ t ′ = t T γ t ′ − t r t \sum\limits_{t' = t}^T {{\gamma ^{t' - t}}} {{\bf{r}}_{\bf{t}}} t′=t∑Tγt′−trt, γ \gamma γ表示衰减系数。该式表示只计算t时刻之后的回报,即未来不影响过去。
在后续提出的诸多改进算法中将权重项写作 A θ ( s t , a t ) {A^\theta }({s_t},{a_t}) Aθ(st,at),称作优势函数(Advantage function),可以理解为处于状态 s时采取 a 相较其他动作的优势。