强化学习入门(四)策略梯度方法 Policy Gradient 求解强化学习问题
本文内容源自百度强化学习 7 日入门课程学习整理
感谢百度 PARL 团队李科浇老师的课程讲解
文章目录
- 一、回顾 Value-based 和 Policy-based
- 1.1 基本概念
- 1.2 区别
- 二、Policy Gradient 算法
- 2.1 随机策略中的 softmax 函数
- 2.2 一局游戏 episode
- 2.3 轨迹的期望回报
- 2.4 优化策略函数
- 三、采样方式:REINFORCE
- 3.1 蒙特卡洛 MC 与 时序差分 TD
- 3.2 REINFORCE 算法
- 四、数据处理技巧
- 4.1 简单场景的图片预处理
- 4.2 使用衰减 reward 并 normalize reward
- 五、Policy Gradient 代码详解
一、回顾 Value-based 和 Policy-based
1.1 基本概念
-
基于价值
- 优化策略价值函数,即 Q 的函数
- 优化好了以后,直接选取最优路径即可
- 如:Sarsa,Q-learning,DQN
-
基于策略
- 不依赖于价值函数
- 一个策略走到底,看最后的总收益来决定该动作的好坏
- 如:Policy Gradient
1.2 区别
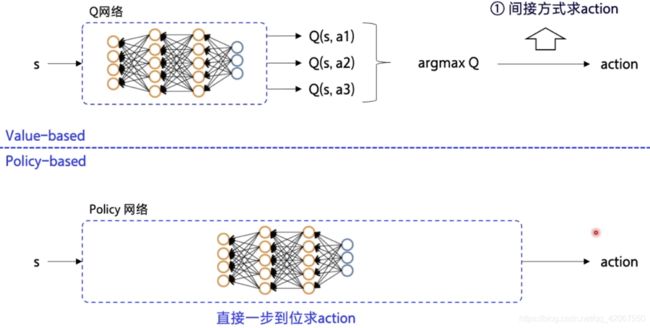
- Value-based:神经网络输入状态 S,输出 Q,优化的也是 Q 函数
- 动作的输出要看最大的 Q 值,所以是间接输出动作
- Policy-based:输入状态 S,输出动作 A
-
Value-based:先优化 Q 函数
- 优化到最优的时候,Q 表固定
- 根据 Q 表得到最优动作
- 所以动作选择是固定的,即确定性策略
-
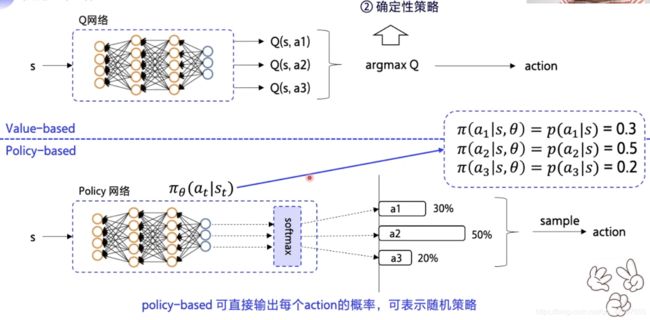
Policy-based:输出动作的概率
- 这里我们用 π θ ( a t ∣ s t ) π_θ(a_t|s_t) πθ(at∣st) 表示 policy 策略, θ θ θ 是神经网络的参数,在 s t s_t st 状态下,做出 a t a_t at 动作的概率
- 所以如果我们在一个状态下只有 3 个动作,则可以表示为:
π ( a 1 ∣ s , θ ) = p ( a 1 , s ) = 0.3 π ( a 2 ∣ s , θ ) = p ( a 2 , s ) = 0.5 π ( a 3 ∣ s , θ ) = p ( a 3 , s ) = 0.2 π(a_1|s,θ) = p(a_1,s)=0.3 \\ π(a_2|s,θ) = p(a_2,s)=0.5 \\ π(a_3|s,θ) = p(a_3,s)=0.2 π(a1∣s,θ)=p(a1,s)=0.3π(a2∣s,θ)=p(a2,s)=0.5π(a3∣s,θ)=p(a3,s)=0.2
二、Policy Gradient 算法
2.1 随机策略中的 softmax 函数
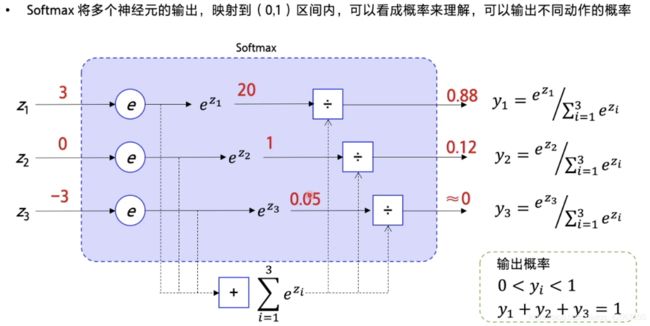
softmax 的作用,就是把输出映射到 0~1 的区间内,并使得所有的输出相加等于 1,于是就可以等同于不同选择的概率了
- 常常用于分类任务
计算方法:
- 每个输出值求一个自然对数
- 然后除以所有输出的自然对数的和
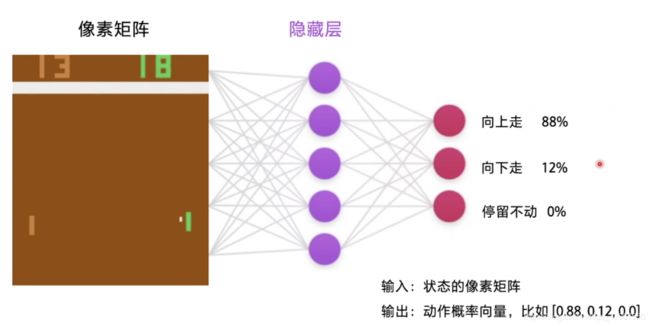
- 输入的是游戏图像(像素矩阵)
- 输出的是动作选择概率(向上 88%,向下 12%,停留不动 0%),向量形式:[0.88, 0.12, 0]
- 然后根据概率随机挑选动作
2.2 一局游戏 episode
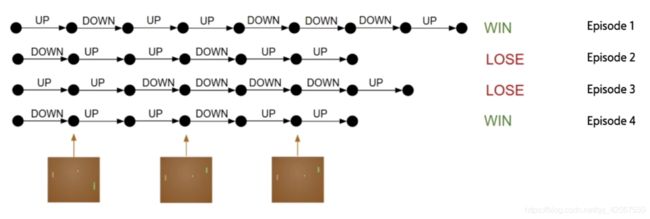
当我们选择一个动作以后,其实并不知道动作的优劣,而只有最终游戏结束得到结果的时候,我们才能反推之前的动作优劣
- 每一个 episode 中,agent 不断和环境交互,输出动作,直到该 episode 结束
- 然后开启另一个 episode
优化策略的目的:让 “每一个” episode 的 “总的” reward 尽可能大
- 单个 episode 有很多 step 组成,每个 step 会获得 reward
- 所有 episode 总的 reward 希望最大
- 所以怎么去量化我的优化目标就是个难点!
2.3 轨迹的期望回报
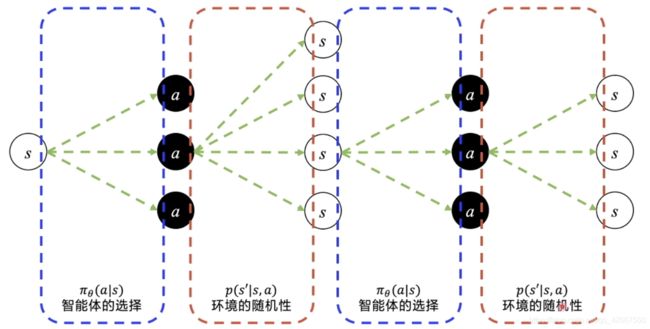
-
从初始状态出发,有不同的概率选择动作
-
然后状态发生变化(环境的随机性,会导致环境的变化也是个概率分布,即状态转移概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a))
-
在新的状态下,再通过不同概率选择动作
-
状态继续发生变化
- 这里我们能够优化的是智能体的选择,而环境的随机变化(状态转移概率)是客观存在的,无法优化(控制)
-
不断地交互,直到完成一个 episode(一局游戏结束)
-
把这个 episode 中所有的连续的 s 变化 和 a 选择串起来,就是一个 episode 的轨迹 Trajectory
-
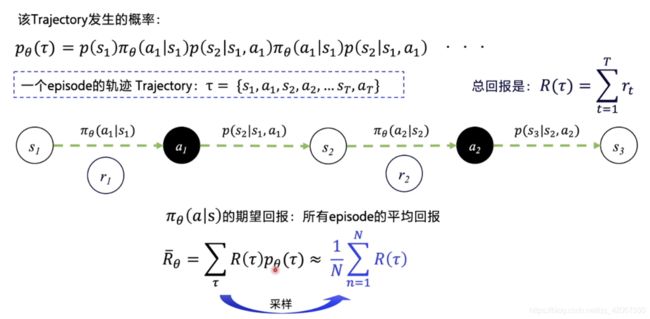
轨迹: τ = { s 1 , a 1 , s 2 , a 2 , . . . s T , a T } τ\ =\ \{s_1,a_1,s_2,a_2,...s_T,a_T\} τ = {s1,a1,s2,a2,...sT,aT}
轨迹的概率:
- 轨迹的每一步概率连乘即可:
- p θ ( τ ) = p ( s 1 ) π θ ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) π θ ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) . . . p_θ(τ)\ = \ p(s_1)π_θ(a_1|s_1)p(s_2|s_1,a_1)π_θ(a_1|s_1)p(s_2|s_1,a_1)... pθ(τ) = p(s1)πθ(a1∣s1)p(s2∣s1,a1)πθ(a1∣s1)p(s2∣s1,a1)...
轨迹的总 reward:
- 即每一步获得的 reward 之和
- R ( τ ) = ∑ t = 1 T r t R(τ)\ = \ \sum_{t=1}^Tr_t R(τ) = ∑t=1Trt
我们和环境交互的轨迹可以有千千万万条,所以当我们跑了很多 episode ,获得许多轨迹后,我们可以获得 “期望回报”:
-
π θ ( a ∣ s ) π_θ(a|s) πθ(a∣s) 的期望回报:所有 episode 的平均回报
-
R θ ‾ = ∑ τ R ( τ ) p θ ( τ ) \overline{R_θ}\ =\ \sum_{τ}R(τ)p_θ(τ) Rθ = ∑τR(τ)pθ(τ)
-
策略 π θ ( a ∣ s ) π_θ(a|s) πθ(a∣s) 下的期望回报就可以用来评价我们的策略优劣
难点:
- 无法穷举所有的轨迹
- 无法获得 “环境转移概率”
解决方法:取近似值
- R θ ‾ = ∑ τ R ( τ ) p θ ( τ ) ≈ 1 N ∑ n = 1 N R ( τ ) \overline{R_θ}\ =\ \sum_{τ}R(τ)p_θ(τ)\ \approx\ {1\over N}\sum_{n=1}^NR(τ) Rθ = ∑τR(τ)pθ(τ) ≈ N1∑n=1NR(τ)
- 这里我们取得 N 条轨迹后(N足够大),假设每条轨迹都是概率相等(随机)
- 这个过程称作:采样(采样 N 个 episode 来计算期望回报)
- 这样就不需要知道 “环境转移概率” 了
2.4 优化策略函数
我们可以用期望回报 R θ ‾ \overline{R_θ} Rθ 来优化策略函数 π θ ( s , a ) π_θ(s,a) πθ(s,a)
-
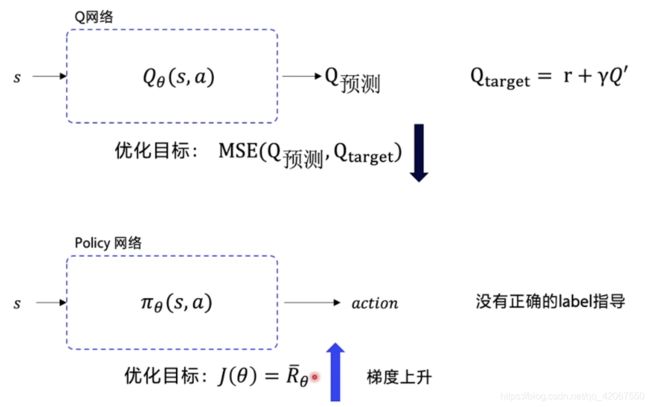
在 DQN 中,我们的 loss 函数是来源于 目标 Q 和 预测 Q 之间的差别,我们希望优化过程是 预测 Q 不断逼近 目标 Q,降低 loss(越小越好)
-
所以在 DQN 中,目标 Q 担任的是一个正确的 label 指导
-
但是在 Policy 网络中,没有这样一个 正确的 label 指导
-
所以需要用到 R θ ‾ \overline{R_θ} Rθ
优化目标:
- J ( θ ) = R θ ‾ J(θ)\ =\ \overline{R_θ} J(θ) = Rθ 越大越好
- 这里是一个梯度上升过程
策略梯度:
- 我们需要求解 R θ ‾ \overline{R_θ} Rθ 对与 θ θ θ 的梯度,用这个梯度去更新网络
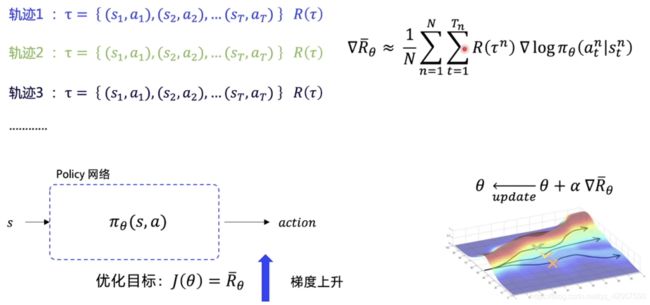
- 首先需要产生 N 条 episode 轨迹
- 每一条轨迹获有一个总回报 R ( τ ) R(τ) R(τ)
- 获得期望回报 R θ ‾ \overline{R_θ} Rθ
- 然后求 R θ ‾ \overline{R_θ} Rθ 对与 θ θ θ 的导数
- ▽ R θ ‾ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ▽ log π θ ( a t n ∣ s t n ) \triangledown \overline{R_θ}\ \approx\ {1\over N}\sum_{n=1}^N\sum_{t=1}^{T_n}R(τ^n)\triangledown \logπ_θ(a_t^n|s_t^n) ▽Rθ ≈ N1∑n=1N∑t=1TnR(τn)▽logπθ(atn∣stn)
- 求导的过程中,可以约去不可知的 “环境转移概率”
- 更新网络后,让分数高的轨迹概率可以更大
- 所以 loss 的公式前面要加上负号,这样就可以让梯度下降变成梯度上升
- L o s s = − R ( τ ) log π θ ( a t ∣ s t ) Loss = -R(τ)\log π_θ(a_t|s_t) Loss=−R(τ)logπθ(at∣st)
三、采样方式:REINFORCE
3.1 蒙特卡洛 MC 与 时序差分 TD
- 蒙特卡洛:算法完成一个 episode,进行学习一次 learn()
- 完整运行一个 episode,我们可以知道每一步 step 的未来总收益 G t G_t Gt
- 比如 :REINFORCE 算法(最简单,经典)
- 时序差分:
- 每一个 step 都更新一次,更新频率更高
- 使用 Q 函数来近似表示未来总收益
- 比如:Actor-Critic 算法
3.2 REINFORCE 算法
- 首先拿到每一步的收益 [ r 1 , r 2 , r 3 . . . r T ] [r_1, r_2,r_3...r_T] [r1,r2,r3...rT]
- 那自然可以计算出每一步的未来总收益 [ G 1 , G 2 , G 3 . . . G T ] [G_1,G_2,G_3...G_T] [G1,G2,G3...GT]
- 未来总收益,代表的是每一个动作的真正价值
- 这样就可以把每一个 G t G_t Gt 代入公式 ▽ R θ ‾ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n G t n ▽ log π θ ( a t n ∣ s t n ) \triangledown \overline{R_θ}\ \approx\ {1\over N}\sum_{n=1}^N\sum_{t=1}^{T_n}G_t^n\triangledown \logπ_θ(a_t^n|s_t^n) ▽Rθ ≈ N1∑n=1N∑t=1TnGtn▽logπθ(atn∣stn) 去优化每一个 action 的输出
def calc_reward_to_go(reward_list, gamma=1.0):
for i in range(len(reward_list) - 2, -1, -1):
# G_t = r_t + γ·r_t+1 + ... = r_t + γ·G_t+1
reward_list[i] += gamma * reward_list[i + 1] # Gt
return np.array(reward_list)
这里的代码就是把每一步的收益,转成每一步的未来总收益
连续的 step 之间未来总收益有相关性: G t = ∑ t = k + 1 T γ k − t − 1 r t = r t + γ G t + 1 G_t\ = \ \sum_{t=k+1}^Tγ^{k-t-1}r_t\ =\ r_t\ +\ γG_{t+1} Gt = ∑t=k+1Tγk−t−1rt = rt + γGt+1
所以在代码实现上,是从后往前计算,先计算 G T G_T GT,再计算 G T − 1 G_{T-1} GT−1,依次进行
假设实际执行的动作 a t a_t at 是 [0,1,0],计算得到的概率 π ( a ∣ s , θ ) π(a|s,θ) π(a∣s,θ) 是 [0.2,0.5,0.3],对每一个 action: L o s s = − G t ⋅ [ 0 , 1 , 0 ] ⋅ log [ 0.2 , 0.5 , 0.3 ] Loss = -G_t\ ·\ [0,1,0]\ ·\ \log[0.2,0.5,0.3] Loss=−Gt ⋅ [0,1,0] ⋅ log[0.2,0.5,0.3]
类比监督学习:
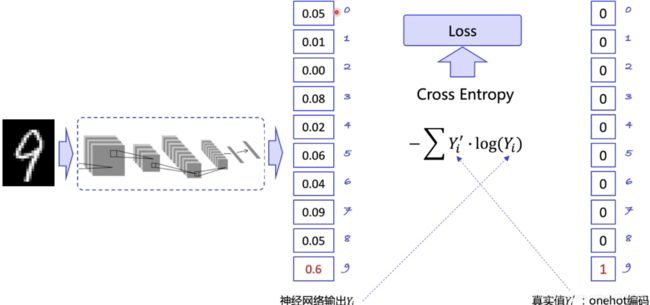
- 输出的概率分布要尽可能贴近真实的情况
- 比如手写数字识别中,如果一个数字是 8,那网络预测这个数字概率越高越好,比如 0.999 ,真实值 8 对应的是 1
- 通过迭代更新,希望识别 8 的时候,这个概率可以远高于其他数字的概率
- 这里我们使用交叉熵 Cross Entropy表示两个概率分布之间的差别
- 目标是缩小差距,即把 Loss 传入优化器自动优化
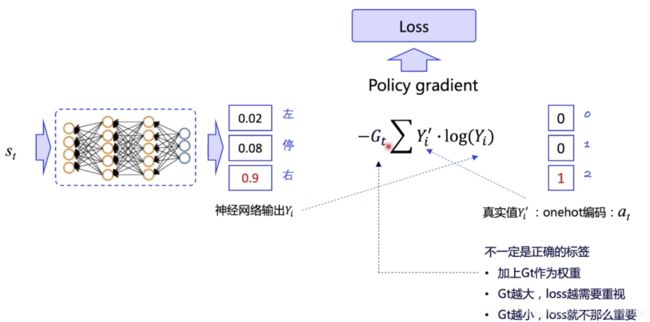
Policy Gradient 中:
- 输出预测行动的概率,和真实采用的概率做比较
- 真实采用的动作是随机选择的 action,并不代表正确的 action
- 所以前面要乘以一个累计回报 G t G_t Gt 作为对真实所采用的 action 的评价
- G t G_t Gt 越大,说明当前输出的 action 是优质的,我们就越是希望预测概率向实际动作逼近
- G t G_t Gt 越小,说明当前输出的 action 不好,所以 loss 的权重也更小,即不强求预测概率向该动作逼近
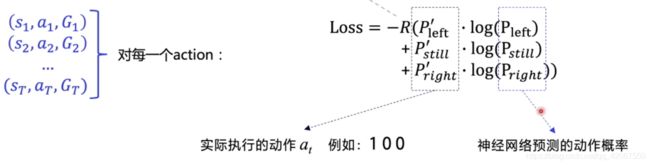
- L o s s = − R ( P l e f t ′ ∗ log ( P l e f t ) + P s t i l l ′ ∗ l o g ( P s t i l l ) + P r i g h t ′ ∗ log ( P r i g h t ) ) Loss = -R(P'_{left}\ * \ \log (P_{left})\ +\ P'_{still}\ *\ log(P_{still})\ +\ P'_{right}\ *\ \log(P_{right})) Loss=−R(Pleft′ ∗ log(Pleft) + Pstill′ ∗ log(Pstill) + Pright′ ∗ log(Pright))
- 其中 R = G t R=G_t R=Gt, P ′ P' P′代表实际执行的动作 a t a_t at(是 one-hot 向量,比如 [0,1,0] ), P P P 代表神经网络预测的动作概率(比如 [0.5, 0.3, 0.2] )
- 由于我们可以拿到 episode 的整个轨迹,所以可以对这个 episode 中每一个 action 都计算一个 Loss
- 累加所有的 Loss,然后让优化器去优化
def learn(self, obs, action, reward): # 输入的就是获得的轨迹,reward代表未来总收益
""" 用policy gradient 算法更新policy model
"""
act_prob = self.model(obs) # 获取输出动作概率(由神经网络预测得到)
# log_prob = layers.cross_entropy(act_prob, action) # 交叉熵
log_prob = layers.reduce_sum(
-1.0 * layers.log(act_prob) * layers.one_hot(
action, act_prob.shape[1]),
dim=1)
cost = log_prob * reward # 乘的是当前 action 的未来总收益
cost = layers.reduce_mean(cost) # 所有 step 要取均值
optimizer = fluid.optimizer.Adam(self.lr)
optimizer.minimize(cost)
return cost
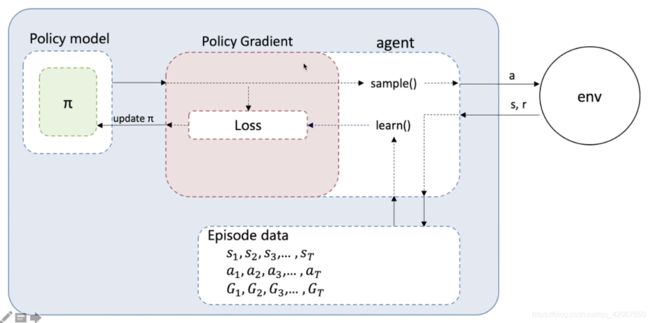
- 首先要有一个 Policy Model 来输出动作概率
- 用 sample() 函数得到具体的动作
- 动作和环境交互,得到 reward
- 一个 episode 运行完,得到轨迹数据(包含 3 个 list:S,a,G)
- 执行 learn() 函数,用轨迹数据构造 loss 函数(该部分可以进行抽取封装)
- loss 函数放入优化器进行优化
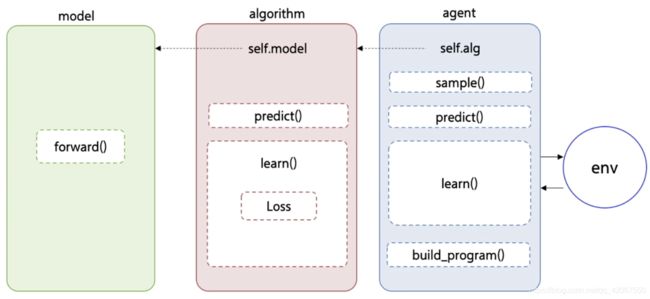
分成了 model,algorithm,agent 三个类
- model 定义网络结构
- algorithm 预测动作输出,构造 loss 函数,实现 learn() 函数
- agent 实现执行动作,和环境交互,获取环境数据
四、数据处理技巧
4.1 简单场景的图片预处理
- 把图片转为灰度
- resize 到 80 * 80 * 1 的形状
- 最后把图片转为 1 维向量
比如在 Pong 的乒乓球游戏环境中:
# Pong 图片预处理
def preprocess(image):
""" 预处理 210x160x3 uint8 frame into 6400 (80x80) 1维 float vector """
image = image[35:195] # 裁剪
image = image[::2,::2,0] # 下采样,缩放2倍
image[image == 144] = 0 # 擦除背景 (background type 1)
image[image == 109] = 0 # 擦除背景 (background type 2)
image[image != 0] = 1 # 转为灰度图,除了黑色外其他都是白色
return image.astype(np.float).ravel()
当然我们也可以用 CNN 网络,但是对于简单图像的环境,其实也可以这样处理,就不用 CNN 网络了
4.2 使用衰减 reward 并 normalize reward
因为有些游戏一个 episode 的时间很长,比如乒乓球游戏 Pong,一方拿到 21 分游戏才结束,所以整个过程有非常多的 step
所以要设计一个衰减因子,不需要考虑太长时间以后的收益,一般会设置为 0.99
另外需要对一个 episode 拿到的收益做 normalize,让我们获取的收益有正有负,基本在原点两侧均衡分布
通常这种归一化的做法是为了加速训练,对于 action 的快速收敛更有效果
# 根据一个episode的每个step的reward列表,计算每一个Step的Gt
def calc_reward_to_go(reward_list, gamma=0.99):
"""calculate discounted reward"""
reward_arr = np.array(reward_list)
for i in range(len(reward_arr) - 2, -1, -1):
# G_t = r_t + γ·r_t+1 + ... = r_t + γ·G_t+1
reward_arr[i] += gamma * reward_arr[i + 1]
# normalize episode rewards
reward_arr -= np.mean(reward_arr)
reward_arr /= np.std(reward_arr)
return reward_arr
五、Policy Gradient 代码详解
强化学习算法 Policy Gradient 解决 CartPole 问题,代码逐条详解