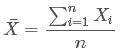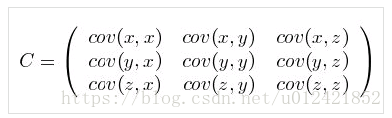【机器学习】【线性代数】均值，无偏估计，总体/样本方差，样本标准差，矩阵中心化/标准化、协方差，正/不/负相关等，协方差矩阵
本篇是概念讲解，协方差以及协方差矩阵的Python实现代码详见：【机器学习】【线性代数】协方差+协方差矩阵的多种求解方法的Python实现（公式法 + 样本集中心化方法 + np.cov()法等）
0.英文chart
mean，均值
variance，方差
standard deviation，标准差
covariance，协方差
covariance matrix，协方差矩阵
1.均值
其中
为样本均值，X是样本变量，n为样本总数
2.总体方差
variance，方差。方差用来衡量一组数据的离散程度。概率论中方差用来度量随机变量和此组随机变量的数学期望(就是均值)之间的偏离程度。方差是衡量源数据和期望值相差的度量值：比如两组数据A和B，A组的方差值为a，B组的方差值为b，如果a>b，说明A组数据和A组的均值的偏离程度 比 B组数据和B组均值的偏程度更严重。
3.样本方差
在实际工作中，一般用样本替代总体。经过校正后，样本方差计算公式为：
无偏估计的计算公式：
为样本方差，X为样本变量，为样本均值，n为样本总数
基于样本中心化的公式：
4.样本标准差
基于样本中心化的公式：
其中s为样本标准差，X为样本变量，为样本均值，n为样本总数。之所以除以n-1而不是除以n，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上所谓的“无偏估计”。而方差只是标准差的平方而已。
标准差描述的是样本的离散度，举例说明：
A=[0，8，12，20]和B=[8，9，11，12]，均值都是10，A的标准差是8.3，B的标准差是1.8，从肉眼看也知道B较为集中，可以知道计算出来的B的标准差也一定比A的标准差小一些。通过上面示例可以形象地直到标准差描述的就是样本中所有样例的离散度，所有样例越不集中，就越离散，则对应的样本的标准差就越大。
标准差和方差一般是用来描述一维数据的，如果我们要描述两个样本之间的关系，就需要用到协方差了。
5.协方差
协方差用来衡量两个变量的总体误差。而方差是协方差的一种特殊情况：即当两个变量是相同的情况。
基于样本集的中心化的协方差公式：
概念：
从直观上来看，协方差表示的是两个变量总体误差的期望
6.协方差和不相关、正相关、负相关
Cov(X,Y)数值表示X和Y的相关性。
假如X代表女人的颜值高低，Y代表男人对女人的喜欢程度。
Cov(X,Y)>0，表明女人颜值越高，男人越喜欢女人，即X和Y是正相关。
Cov(X,Y)<0，表明女人颜值越高，男人越讨厌女人，即X和Y是负相关。
Cov(X,Y)=0，表明女人颜值高不高，和男人喜欢不喜欢，没有任何关联关系。
7.协方差矩阵
协方差Cov(X,Y)只能处理二维问题，比如女人颜值和男人的喜爱的相关度，如果要处理多维问题，就需要用到协方差矩阵了。
数据集{x,y,z}，有三个维度。这三个维度之间的相关可以用数据集的协方差矩阵来表示，如下所示：
协方差有如下两个公式成立：
可以很容易知道：
（1）协方差矩阵是一个对称阵
（2）协方差矩阵的对角线上的元素是每个维度的方差
（3）协方差矩阵计算的是一个样本中不同维度之间的协方差，而不是两个或多个样本之间的协方差
（4）此处所说的维度就是样例的一个特征，比如一个样本是10*3大小，则表示有10个样例，每个样例有3个特征
8.矩阵中心化
样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0。
从几何意义来讲，矩阵中心化就是使得样本矩阵的中心回归到坐标系的原点。
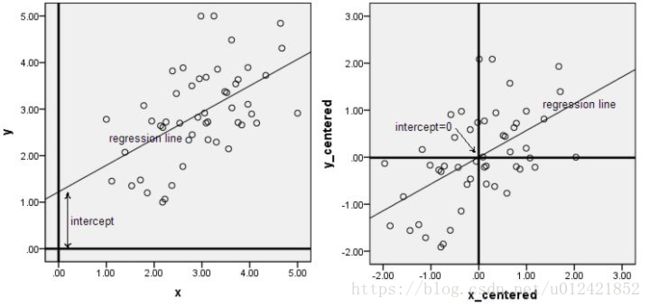
下图来自知乎：数据什么时候需要做中心化和标准化处理？
此图形象的表述了，矩阵中心化的几何意义，就是讲样本集的中心平移到坐标系的原点O上。
注：数据中心化和数据标准化的目标区别
（1）对数据进行中心化预处理，这样做的目的是要增加基向量的正交性。
（2）对数据标准化的目的是消除特征之间的差异性。便于对一心一意学习权重。
参考文献：
[1]百度百科
[2]浅谈协方差矩阵，这个总结的不错~
(end)