强化学习(Reinforcement Learning)学习笔记DAY01（RL分类和Q Learning简单例子）

分类

可以把所有的强化学习分成两类：Model-Free RL和Model-Based RL。

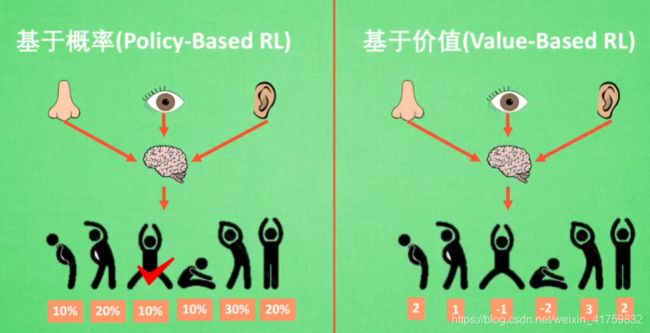
还可以分成以下两类：基于概率（Policy-Based RL）和基于价值（Value-Baesd RL）。

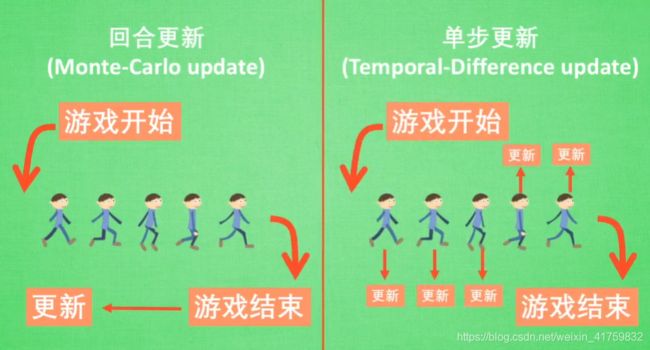
还有另外一种分类：回合更新（Monte-Carlo update）和单步更新（Temporal-Difference update）。

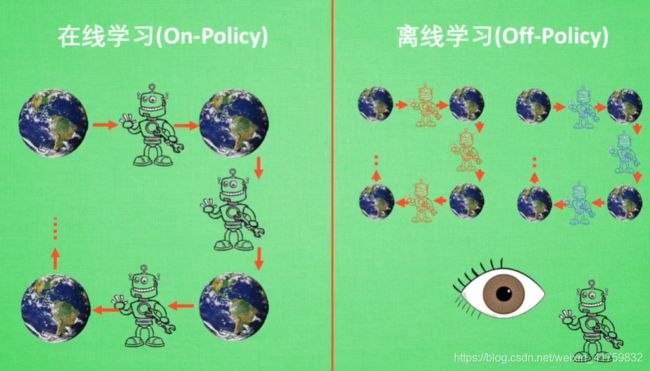
要说的最后一种分类：在线学习（On-Policy）、离线学习（Off-Policy）。

Model-Based与Model-Free

可参考https://blog.csdn.net/broadview2006/article/details/100556095

Model-Based能通过想象来预判接下来遇到的所有情况。然后根据想象中的情况选择最好的那种，并根据这种情况采取下一步的策略。

Model-free类似黑盒，整个Model是未知的，只能按部就班，一步一步等待真实世界的反馈来设置学习策略，进行下一步行动。

---

Policy-Based RL和Value-Baesd RL

连续的动作不能用基于价值的方法来做。

Policy-Based RL方法：Policy Gradients。

Value-Baesd  RL方法：Q Learning、Sarsa。

结合两种的方法：Actor-Critic。

Actor会基于概率做出动作，Critic会对于做出的动作给出动作的价值。

---

Monte-Carlo update和Temporal-Difference update

Monte-Carlo update指的是游戏开始后到游戏结束，总结回合中所有的转折点，再更新我们的行为准则。

方法：基础版Policy Gradiente、Monte-Carlo learning。

Temporal-Difference update指的是在游戏过程中每一步都在更新，不用等待游戏的结束，便可以边玩边学习了。

方法：升级版Policy Gradiente、Q learning、Sarsa。

---

On-Policy和Off-Policy

所谓的在线学习就是必须本人在场，而且必须是本人边玩边学习。离线学习则是可以自己玩也可以看着别人玩。

On-Policy方法：Sarsa、Sarsa(λ)。

Off-Policy方法：Q Learning、Deep Q Network。

---

Q Learning

Q Learning算法：

参数意义：

• -greedy是用在决策上的一种策略，等于0.9时就说明90%的情况会按照Q表的最优值来选择行为，10%的情况选择随机行为。
• α是学习效率，来决定这一次的误差有多少要学习。
• γ是对未来的衰减值。

---

Q Learning简单例子

根据以上算法写代码：

import numpy as np
import pandas as pd
import time

np.random.seed(2) #产生一组伪随机数列，每次运行随机过程都是一样的

N_STATES = 6      # 离宝藏的距离有多少步
ACTIONS = ['left', 'right']     # 两个动作（左+右）
EPSILON = 0.9   # 0.9最优动作+0.1随机动作
ALPHA = 0.1     # learning rate
GAMMA = 0.9    # discount factor
MAX_EPISODES = 13   # maximum episodes 只玩13回合
FRESH_TIME = 0.01    # fresh time for one move 走一步花的时间有多长


def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),    # q_table initial values
        columns=actions,      # actions's name
    )
    print(table)
    return table


def choose_action(state, q_table):
    # This is how to choose an action
    state_actions = q_table.iloc[state, :]
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):  # act non-greedy or state-action have no value
        action_name = np.random.choice(ACTIONS)
    else:   # act greedy
        action_name = state_actions.idxmax()    # replace argmax to idxmax as argmax means a different function in newer version of pandas
    return action_name

def get_env_feedback(S, A): #获得行为奖励R和下一个state
    # This is how agent will interact with the environment
    if A == 'right':    # move right
        if S == N_STATES - 2:   # terminate
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:   # move left
        R = 0
        if S == 0:
            S_ = S  # reach the wall
        else:
            S_ = S - 1
    return S_, R

def update_env(S, episode, step_counter):  #建立环境，没必要具体看
    # This is how environment be updated
    env_list = ['-']*(N_STATES-1) + ['T']   # '---------T' our environment
    if S == 'terminal':
        interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                                ', end='')
    else:
        env_list[S] = 'o'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)


def rl():
    # main part of RL loop
    q_table = build_q_table(N_STATES, ACTIONS) #创建qtable
    for episode in range(MAX_EPISODES):
        step_counter = 0
        S = 0       #初始状态
        is_terminated = False  #是否为终止符
        update_env(S, episode, step_counter)  #更新环境
        while not is_terminated:

            A = choose_action(S, q_table)  #根据初始state选择action
            S_, R = get_env_feedback(S, A) #获得行为奖励R和下一个state
            q_predict = q_table.loc[S, A]  #估计值
            if S_ != 'terminal':
                q_target = R + GAMMA * q_table.iloc[S_, :].max() #真实值
            else:
                q_target = R     # next state is terminal
                is_terminated = True #回合终止后没有下一个的qnext，改为终止跳出循环

            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  # update
            S = S_  # move to next state

            update_env(S, episode, step_counter+1)  #探索者走了每一步再更新环境
            step_counter += 1
    return q_table

if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

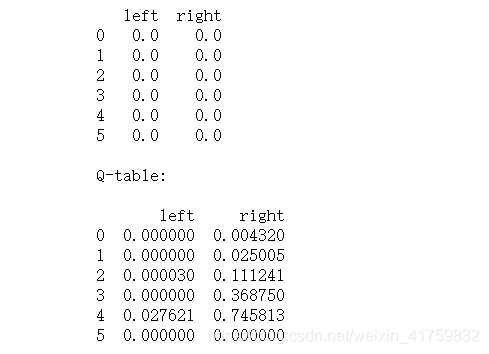
运行结果如下：

 

可见qtable的左边都是比右边要小的，因为有90%概率选到朝右走的值。