强化学习入门

参考：

1. https://zhuanlan.zhihu.com/sharerl
2. https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/2-1-A-q-learning/

马尔科夫决策过程

强化学习原理

图1.1 强化学习原理解释

图1.1解释了强化学习的基本原理。智能体在完成某项任务时，首先通过动作A与周围环境进行交互，在动作A和环境的作用下，智能体会产生新的状态，同时环境会给出一个立即回报。如此循环下去，智能体与环境进行不断地交互从而产生很多数据。强化学习算法利用产生的数据修改自身的动作策略，再与环境交互，产生新的数据，并利用新的数据进一步改善自身的行为，经过数次迭代学习后，智能体能最终地学到完成相应任务的最优动作（最优策略）。

马尔科夫性

马尔科夫性是指系统的下一个状态$s_{t+1}$仅与当前状态$s_t$有关，而与以前的状态无关。

定义：状态$s_t$是马尔科夫的，当且仅当$P[s_{t+1}|s_t]=P[s_{t+1}|s_1,s_2,...,s_t]$。

马尔科夫性描述的是每个状态的性质，但真正有用的是如何描述一个状态序列。数学中用来描述随机变量序列的学科叫随机过程。所谓随机过程就是指随机变量序列。若随机变量序列中的每个状态都是马尔科夫的则称此随机过程为马尔科夫随机过程。

马尔科夫过程

马尔科夫过程是一个二元组$(S,P)$，且满足：$S$是有限状态集合， $P$是状态转移概率。状态转移概率矩阵为：

一个例子：

图1.2 马尔科夫过程示例图

如图1.2所示为一个学生的7种状态{娱乐，课程1，课程2， 课程3，考过，睡觉，论文}，每种状态之间的转换概率如图所知。则该生从课程1开始一天可能的状态序列为：

课1-课2-课3-考过-睡觉

课1-课2-睡觉

以上状态序列称为马尔科夫链。当给定状态转移概率时，从某个状态出发存在多条马尔科夫链。对于游戏或者机器人，马尔科夫过程不足以描述其特点，因为不管是游戏还是机器人，他们都是通过动作与环境进行交互，并从环境中获得奖励，而马尔科夫过程中不存在动作和奖励。将动作（策略）和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。

马尔科夫决策过程（MDP）

马尔科夫决策过程由元组$(S,A,P,R,\gamma )$描述，其中：$S$为有限的状态集, $A$为有限的动作集, $P$为状态转移概率, $R$为回报函数, $\gamma$为折扣因子，用来计算累积回报。注意，跟马尔科夫过程不同的是，马尔科夫决策过程的状态转移概率是包含动作的即：

$P_{s{s}^{\prime }}^a=P[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$。

一个例子：

图1.3 马尔科夫决策过程示例图

图1.3为马尔科夫决策过程的示例图，图1.3与图1.2对应。在图1.3中，学生有五个状态，状态集为$S=\{s_1,s_2,s_3,s_4,s_5\}$，动作集为$A=\{玩，退出，学习，发论文，睡觉\}$，在图1.3中立即回报用红色标记。

强化学习的目标是给定一个马尔科夫决策过程，寻找最优策略，这里的最优是指得到的总回报最大。所谓策略是指状态到动作的映射，策略常用符号$\pi$表示，它是指给定状态$s$时，动作集上的一个分布，即：

$\pi (a|s)=p[A_t=a|S_t=s]$

当给定一个策略$\pi$时，我们就可以计算累积回报了。首先定义累积回报：

$G_t=R_{t+1}+\gamma R_{t+2}+...=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$

当智能体采用策略$\pi$时，累积回报服从一个分布，累积回报在状态$s$处的期望值定义为状态值函数：

$v_{\pi }(s)=E_{\pi }[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s]$

注意：状态值函数是与策略$\pi$相对应的，这是因为策略$\pi$决定了累积回报$G$的状态分布。

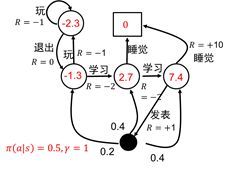
图1.4 状态值函数示意图

如图1.4所示为状态值函数图。图中白色圆圈中的数值为该状态下的值函数。

$v(s_4)=0.5\ast (1+0.2\ast (-1.3)+0.4\ast 2.7+0.4\ast (7.4))+0.5\ast 10=7.39$

相应地，状态行为值函数为：

$q_{\pi }(s,a)=E_{\pi }[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a]$

贝尔曼方程

贝尔曼方程用于求解MDP问题，也就是找到最优策略及其对应的价值函数。

$v_{\pi }(s)=E_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]$

$q_{\pi }(s,a)=E_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s,A_t=a]$

最优状态值函数：$v^{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s)$
最优状态行为值函数：$q^{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$

图1.5 最优值函数和最优策略

图1.5为最优状态值函数示意图，图中红色箭头所示的动作为最优策略。

强化学习算法的形式化描述

定义一个离散时间有限范围的折扣马尔科夫决策过程$M=(S,A,P,r,{\rho }_0,\gamma ,T)$
S：状态集
A：动作集
P：$S\times A\times S\to R$ 转移概率
r：$S\times A\to [-R_{max},R_{max}]$ 立即回报函数
${\rho }_0$：$S\to R$ 初始状态分布
$\gamma \in [0,1]$：折扣因子
T：水平范围（步数）

强化学习的目标：找到最优策略，使得该策略下的累积回报期望最大。

当值函数最优时采取的策略也是最优的。反过来，策略最优时值函数也最优。

强化学习算法分类

图1.8 强化学习算法分类

如图1.8所示，强化学习算法根据以策略为中心还是以值函数最优可以分为两大类，策略优化方法和动态规划方法。其中策略优化方法又分为进化算法和策略梯度方法；动态规划方法分为策略迭代算法和值迭代算法。策略迭代算法和值迭代算法可以利用广义策略迭代方法进行统一描述。

另外，强化学习算法根据策略是否是随机的，分为确定性策略强化学习和随机性策略强化学习。根据转移概率是否已知可以分为基于模型的强化学习算法和无模型的强化学习算法。另外，强化学习算法中的回报函数十分关键，根据回报函数是否已知，可以分为强化学习和逆向强化学习。逆向强化学习是根据专家实例将回报函数学出来。

基于模型的动态规划算法

基于模型的强化学习可以利用动态规划的思想来解决。顾名思义，动态规划中的动态蕴含着序列和状态的变化；规划蕴含着优化，如线性优化，二次优化或者非线性优化。利用动态规划可以解决的问题需要满足两个条件：整个优化问题可以分解为多个子优化问题；子优化问题的解可以被存储和重复利用。

基于模型的动态规划算法主要有两种：策略迭代和价值迭代。这两种方法大体上类似，均由两个子问题组成：策略评估和策略提升。

策略迭代（Policy Iteration）

策略评估（Policy Evaluation）

$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)q_{\pi }(s,a)$
$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })$

联立可得：

$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$

对于模型已知的强化学习算法，方程中的$R_s^a$，$P_{s{s}^{\prime }}^a$和$\gamma$都是已知数，$\pi (a|s)$为要评估的策略是指定的，也是已知值。方程中唯一的未知数是值函数。可以证明方程有唯一解。但此处，我们使用高斯-赛德尔迭代算法进行求解。

有了上面的迭代算法，任何给定的策略π，我们都可以计算出它的价值函数。

策略提升（Policy Improvement）

我们计算$\pi$的价值函数$v_{\pi }$的目的是为了找到“更好”的策略。对于给定的策略$\pi$和状态$s$，我们知道$v_{\pi }(s)$。如果假设原来的策略是确定的，那么原来的策略是遇到s，会用概率$\pi (a|s)$来选择行为$a^{\prime }$，同时我们也知道在状态$s$下采取$a$并且在后续也使用策略$\pi$的价值(期望的长期回报)：

$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })$

如果这个行为a的价值$q_{\pi }(s,a)>v_{\pi }(s)$，那么我们可以这样构造一个新的策略：在状态s时采取固定的策略a，之后的策略和原来的一样。这个问题可以通过策略提升定理(Policy Improvement Theorem)证明。

---

策略迭代算法包括策略评估和策略改进两个步骤。在策略评估中，给定策略，通过数值迭代算法不断计算该策略下每个状态的值函数，利用该值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。这是一个策略收敛的过程。

策略迭代伪代码：

价值迭代（Value Iteration）

策略迭代的一个问题就是每一次策略的提升都需要计算新策略的价值$v_{\pi }$，计算一个策略的价值本身又需要一次迭代算法。我们有必要精确的知道$v_{\pi }$吗？实际上可能是不需要的，假设策略评估需要100次迭代，那么我们能否只迭代50次就开始策略提升呢？答案是肯定的。更加极端的是只进行一次策略评估就进行策略提升，这就是本节的算法——价值迭代。因为只有一次策略评估，我们可以把它整合到策略提升的公式里，这样看起来我们一种在更新价值，所以这个算法就叫价值迭代。

无模型算法 —— 蒙特卡罗方法

在现实的强化学习任务中，环境的转移概率、奖赏函数甚至状态总数往往很难得知。若学习算法不依赖环境建模，则称为无模型算法。解决无模型的马尔科夫决策问题是强化学习算法的精髓。无模型的强化学习算法主要包括蒙特卡罗方法和时间差分方法。这一节我们先讲蒙特卡罗的方法。

在动态规划的方法中，值函数的计算方法:

$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$

在无模型强化学习中，模型$P_{s{s}^{\prime }}^a$是未知的。回到值函数最原始的定义公式:

$v_{\pi }(s)=E_{\pi }[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s]$

状态值函数和行为值函数的计算实际上是计算返回值的期望。动态规划的方法是利用模型对该期望进行计算。在没有模型时，我们可以采用蒙特卡罗的方法计算该期望，即利用随机样本来估计期望。在计算值函数时，蒙特卡罗方法是利用经验平均代替随机变量的期望。

经验，是指利用该策略做很多次试验，产生很多组数据。

平均就是求均值。不过，利用蒙特卡罗方法求状态$s$处的值函数时，又可以分为第一次访问蒙特卡罗方法和每次访问蒙特卡罗方法。

第一次访问蒙特卡罗方法是指，在计算状态$s$处值函数时，只利用每次试验中第一次访问到状态$s$时的返回值。每次访问蒙特卡罗方法是指，在计算状态$s$处的值函数时，利用所有访问到状态$s$时的回报返回值。

探索性初始化

获得充足的经验是无模型强化学习的核心所在。在动态规划方法中，为了保证值函数的收敛性，算法会对状态空间中的状态进行逐个扫描。无模型的方法充分评估策略值函数的前提是每个状态都能被访问到。因此，在蒙特卡洛方法中必须采用一定的方法保证每个状态都能被访问到。其中一种方法是探索性初始化。

所谓探索性初始化是指每个状态都有一定的几率作为初始状态。这需要策略是温和的，典型的温和策略是$ϵ-soft$策略：

根据探索策略（行动策略）和评估的策略是否是同一个策略，蒙特卡罗方法又分为同策略（on-policy）和异策略（off-policy）。

同策略（On-policy）

伪代码：

同策略蒙特卡罗强化学习算法最终产生的是$ϵ-soft$策略。但引入此策略是为了便于策略评估，而不是为了最终使用。实际上我们希望改进的是原始策略。

异策略（Off-policy）

异策略是指产生数据的策略与评估和改善的策略不是同一个策略。我们用$\pi$表示用来评估和改进的策略，用$\mu$表示产生样本数据的策略。利用行为策略产生的数据评估目标策略需要利用重要性采样方法。

无模型算法 —— 时序差分学习（TD）

蒙特卡罗强化学习需要在完成一个采样轨迹后再更新策略的值估计，而前面介绍的基于动态规划的策略迭代和值迭代算法在每执行一步策略后就进行值函数更新。两者相比，蒙特卡罗强化学习算法效率低得多，这是因为其没有充分利用强化学习任务的MDP结构。时序差分学习则结合了动态规划（bootstrapping 利用后继状态的值函数估计当前值函数）与蒙特卡罗方法（即做试验）的思想，能更高效的免模型学习。

TD方法更新值函数的公式为：

$V(S_t)\leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))$

其中$R_{t+1}+\gamma V(S_{t+1})$称为TD目标，$R_{t+1}+\gamma V(S_{t+1})-V(S_t)$称为TD偏差。

从图中可以看到，蒙特卡罗的方法使用的是值函数最原始的定义，该方法利用所有回报的累积和估计值函数。DP方法和TD方法则利用一步预测方法计算当前状态值函数。其共同点是利用了bootstrapping方法，不同的是，DP方法利用模型计算后继状态，而TD方法利用试验得到后继状态。

Sarsa算法

该算法由于每次更新值函数需知道前一步的状态(state)、前一步的动作(action)、奖赏值(reward)、当前状态(state)、将要执行的动作(action)，由此得名Sarsa算法。Sarsa算法是一个同策略算法，算法中评估、执行的均为$ϵ$贪婪策略。

Q-learning

将Sarsa修改为异策略算法，即得到Q-learning算法。该算法评估是原始策略，执行是$ϵ$贪婪策略。

例子：

根据 Q 表的估计, 因为在 s1 中, a2 的值比较大, 通过之前的决策方法, 我们在 s1 采取了 a2, 并到达 s2, 这时我们开始更新用于决策的 Q 表, 接着我们并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以我们把大的 Q(s2, a2) 乘上一个衰减值 gamma (比如是0.9) 并加上到达s2时所获取的奖励 R (这里还没有获取到我们的棒棒糖, 所以奖励为 0), 因为会获取实实在在的奖励 R , 我们将这个作为我现实中 Q(s1, a2) 的值, 但是我们之前是根据 Q 表估计 Q(s1, a2) 的值. 所以有了现实和估计值, 我们就能更新Q(s1, a2) , 根据估计与现实的差距, 将这个差距乘以一个学习效率 alpha 累加上老的 Q(s1, a2) 的值变成新的值. 但时刻记住, 我们虽然用 maxQ(s2) 估算了一下 s2 状态, 但还没有在 s2 做出任何的行为, s2 的行为决策要等到更新完了以后再重新另外做. 这就是 off-policy 的 Q learning 是如何决策和学习优化决策的过程。

值函数近似

基于动态规划的方法，基于蒙特卡罗的方法和基于时间差分的方法，都有一个基本的前提条件，就是状态空间和动作空间是离散的，而且状态空间和动作空间不能太大。

我们回想一下已经介绍的强化学习方法的基本步骤是：首先评估值函数，接着利用值函数改进当前的策略。其中值函数的评估是关键。对于模型已知的系统，值函数可以利用动态规划的方法得到；对于模型未知的系统，可以利用蒙特卡罗的方法或者时间差分的方法得到。

这时的值函数其实是一个表格。对于状态值函数，其索引是状态；对于行为值函数，其索引是状态-行为对。值函数迭代更新的过程实际上就是对这张表进行迭代更新。因此，之前讲的强化学习算法又称为表格型强化学习。若状态空间的维数很大，或者状态空间为连续空间，此时值函数无法用一张表格来表示。这时，我们需要利用函数逼近的方法对值函数进行表示。

在值函数逼近方法中，值函数对应着一个逼近函数$\hat{v}(s)$ 。从数学角度来看，函数逼近方法可以分为参数逼近和非参数逼近，因此强化学习值函数估计可以分为参数化逼近和非参数化逼近。其中参数化逼近又分为线性参数化逼近和非线性化参数逼近。